第三章:集合与关系
3.1集合的概念与表示法
一、集合的定义、表示法
1.定义:集合是由某些可以互相区分的事物汇聚在一起组成的整体,用A,B,C表示。(注:元素具有确定性和互异性。)
2.有限集合A的元素个数记作 |A| 。
3.集合的表示法(列举法,描述法)。
二、元素与集合关系、集合间关系
4.元素和集合的关系(属于和不属于)
5.集合间的关系(包含、真包含、相等)(全集、空集)
例:

三、幂集的定义
6.幂集:给定集合A,由A的所有的子集作成的集合,称为A的幂集,记作P(A)。
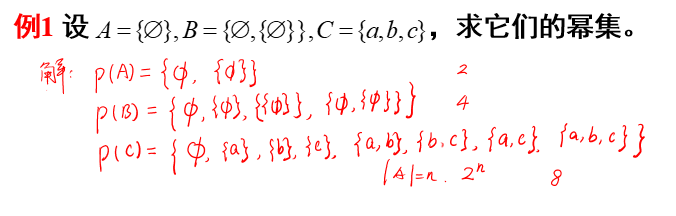
定理1: 设A是有限集合,且 |A| = n,则 |P(A)| = 2的n次方
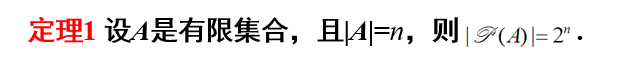
3.2 集合的运算
1 交、并、补、绝对补
2 对称差
3 运算律
4 集合相等的证明方法
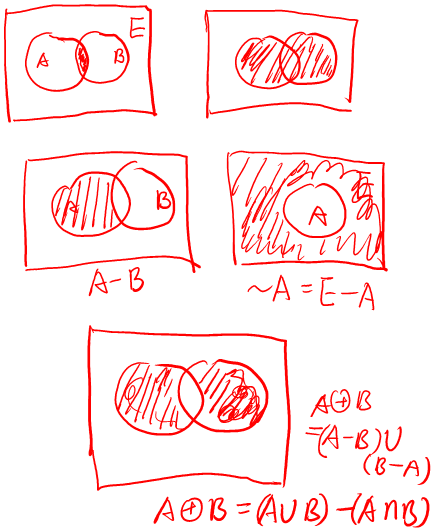
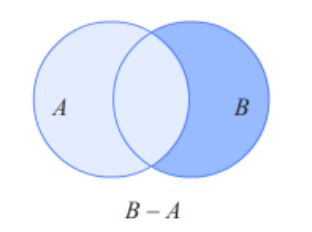
相对补:如果A和B是集合,则在B中的A的相对补集也称为B和A的集合差,其元素属于 B,但不属于 A。A 在B 中的相对补集通常写作B - A,读作“A在B中的相对补集”。
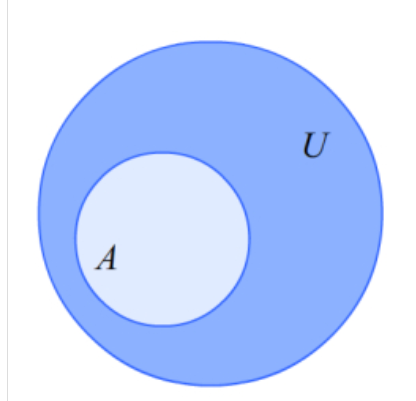
绝对补:U是集合,A是U子集,由U不属于A的元素组成的集合,叫做子集A在U的绝对补集。
对称差:A⊕B表示对称差运算,两个集合的对称差是只属于其中一个集合,而不属于另一个集合的元素组成的集合。(由图示容易理解)

集合的一些等式:
- A - B = A ∩ ~B
- A - B = A - (A∩B)

证明集合等式例题:
思路:利用上面的两个等式将差集运算转化为交集运算,对补运算用德摩根律展开,再根据目标的形式运用 交集/并集 对 并集/交集 的分配律。
3.3 包含排斥原理(容斥原理 )

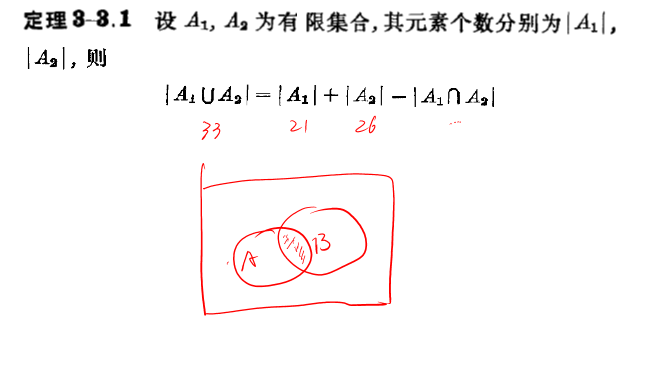
两个集合的容斥原理:
|A∪B| = |A| + |B| - |A∩B|
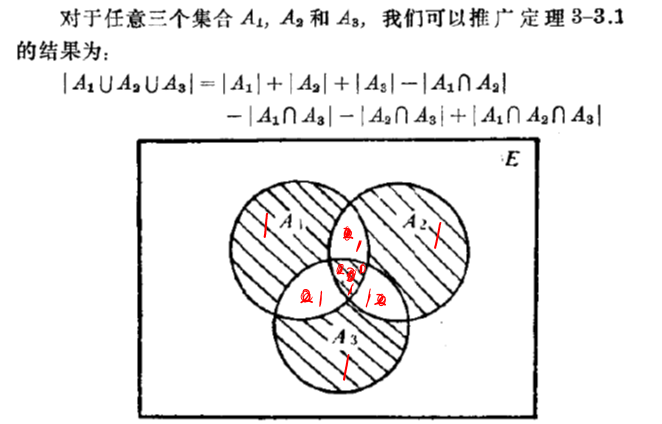
对于三个集合,也有类似的定理:
|A∪B∪C| = |A| + |B| + |C| - |A∩B| - |B∩C| - |A∩C| + |A∩B∩C|
推广到三个以上更多集合时有:
|A1∪A2∪......∪An|
= |A1| + |A2| + ......+ |An| ﹣(|A1∩A2| + |A1∩A3| + ......+ |A[n-1]∩An|) +
(|A1∩A2∩A3| + |A1∩A2∩A4| + ......+ |A[n-2]∩A[n-1]∩An|) + ......+
[(-1)^(n-1)]*|A1∩A2∩......∩An| (注:[n-1],[n-2]为下标;(-1)^(n-1)表示-1的n-1次方)

下面为两道例题:

(注意:要关注题目所求的量的具体含义,(比如:学法语的人数为65,而只学法语的人数为28)
结合文氏图进行求解,使用容斥原理能求出的量往往是为了更好地画出文氏图)

(注意:本题中在算B∩C的元素个数时,分母上[6,8]表示的是6和8的最小公倍数,为24,而不是6×8,[5,6,8]也同理)