已知数组 79、52、48、51、49、34、21、3、26、23 ,请采用堆排序使数组有序。
“什么是堆”
堆是一颗完全二叉树,N层完全二叉树是一颗,除N-1层外其节点数都达到最大,且第N层子节点全部集中在树的最左侧的二叉树。
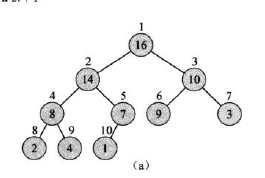
其次一般堆采用数组实现。
故其节点有如下关系:
根节点为ROOT:(X-1)/2;左节点LEFT为:2*X+1;右节点RIGHT为:2*X+2(LEFT+1);
堆分为:“最大堆”,以及“”最小堆”。最大堆是其根节点大于其子节点(每层子树同样是根节点大于其子节点)即 A[PARENT(i)]>=A[i].
最小堆与最大堆的情况相反即 A[PARENT(i)]<=A[i].
堆是一颗 “弱排序”的二叉树,与二叉搜索树不同,堆仅要求根节点大于或等于子节点。(二叉搜索树,左节点<根节点<=右节点)
根据以上性质我们便可以构建“堆”。
在构建堆时采用了两种思想:插入时,将“插入元素放在数组尾端”,根据性质向上搜索,插入合适的位置。即由树脚到树根方向。
删除时,将根节点,弹出后,将数组尾端较小元素放置在根部,然后从树根根据性质向下搜索,插入合适的位置。 即从树根到树脚方向。
堆排序的思想就是利用堆这种数据结构,将待排序的数组插入堆,然后在按序弹出,数组即有序
即 for(){
Heap.Insert(i)
}
for( ){
Heap.popTop();
}
经过以上操作,数组有序。
以下是采用java实现的 (最大堆),输出排序结果为从大到小。
public class HeapOrder {
private int[] Array;
private int currentIndex;
private int maxIndex;
public HeapOrder(int size) {
this.Array = new int[size];
this.currentIndex = 0;
this.maxIndex = size-1;
}
public void insert(int value) {//插入元素,构建最大堆
if(this.maxIndex<this.currentIndex) {
System.out.println("堆已满");
}else {
this.Array[this.currentIndex++] = value;
this.moveUp(this.currentIndex-1); //向上移动元素 从树脚到树根方向
}
}
public int popTop() {//弹出树根,即最大元素
if(this.currentIndex!=0) {
int popValue = this.Array[0];
this.Array[0] = this.Array[--this.currentIndex];
this.moveDown(0); //向下移动元素 从树根到树脚方向
return popValue;
}else {
return -1;
}
}
private void moveUp(int index) {
int temp = this.Array[index];
int root = (index-1)/2;
while(index>0&&temp>this.Array[root]) {//判断元素所在位置,防止越界;同时检查插入元素和其相对树根元素的大小
this.Array[index] = this.Array[root];
index = root;
root = (index-1)/2;
}
this.Array[index] = temp;
}
private void moveDown(int index) {
int temp = this.Array[index];
int largeValue;
while(this.currentIndex/2>index) {//每次循环的子树都必须要至少有一个子节点(左节点)
int left = 2*index+1;
int right = left+1;
if(right<this.currentIndex&&this.Array[left]<this.Array[right]) {//保证有右节点存在,并从左节点和右节点中选择较大的节点
largeValue = right;
}else{
largeValue = left;
}
if(temp>this.Array[largeValue]) {
break;
}else {
this.Array[index] = this.Array[largeValue];
index=largeValue;
}
}
this.Array[index] = temp;
}
最终结果:79、52、51、49、48、34、26、26、21、3
堆排序是一个运行时间为O(N*lgN)的排序算法。