1、定义
二叉树是一颗树,其中每个节点最多有两个子节点(最多2个儿子)
图:
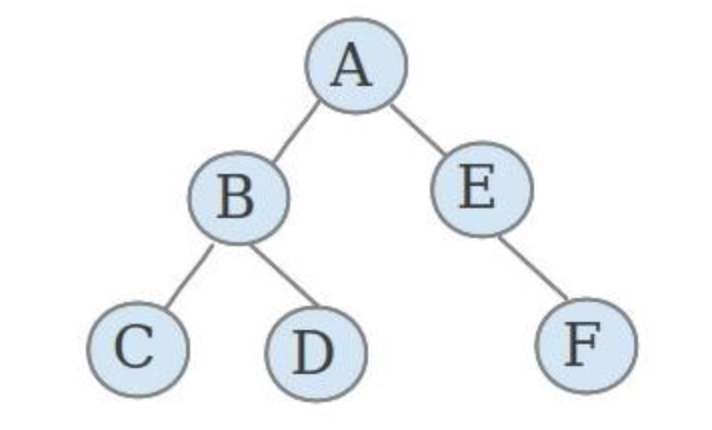
特征:
1.每个节点最多2个儿子。
2.分为左子树和右子树(相对于树来说,一般树不分左子树和右子树,而二叉树一定分左右子树)。
ps
盗图一张:
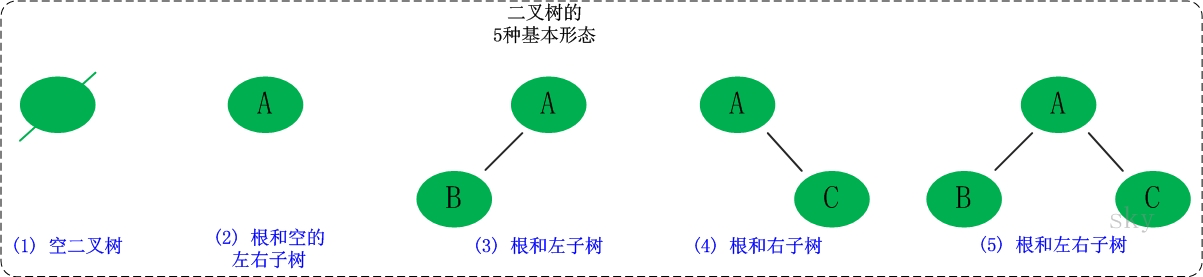
2、二叉树的分类
2.1 满二叉树
特点:N阶的二叉树,除了叶结点外每一个结点都有左右子叶且叶子结点都处在最底层的二叉树。简单来树,树是满的,父节点都有左右子树,不存在只有左子树或者只有右子树的情况

2.2 完全二叉树
特点:
1)只允许最后一层有空缺结点且空缺在右边,即叶子结点只能在层次最大的两层上出现;
2)对任一结点,如果其右子树的深度为j,则其左子树的深度必为j或j+1。 即度为1的点只有1个或0个
简单来树,就是对于N阶的完全二叉树,在N-1层,具有全部节点,在第N层,如果有子节点,那必定是左子树,或者左右子树都存在,而不能只有右子树。
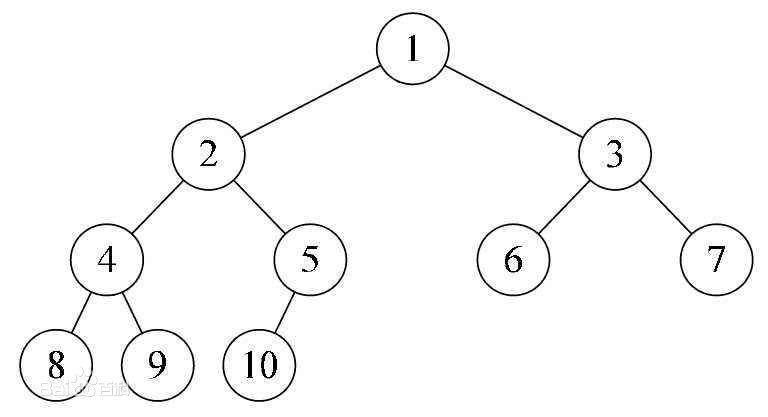
2.3 二叉查找树/二叉搜索树/排序树
特点:
对于每个节点X,它的左子树中所有的项的值小于X的值,右子树所有项的值大于X的值。
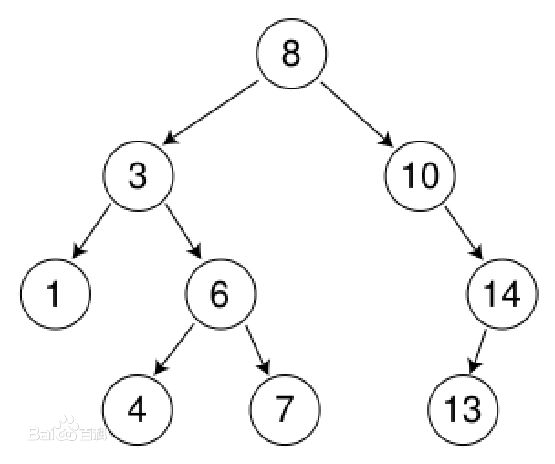
2.4 平衡二叉树
带有平衡条件的二叉查找树 ----- (https://www.cnblogs.com/dhcao/p/10467423.html)
平衡条件:左子树和右子树的高度最多差1
3、二叉树的应用
二叉树在搜索方面的应用不算很重要,它的主要用处之一是在编译器的设计领域。
例子:表达式树 --- (单独解释)
将栈结构与二叉树结构相关联,表达式树的树叶是操作数,其他节点为操作符。使用中序遍历得到中缀表达式,这是跟栈结构可以配合的一种记法。使用后序遍历得到后缀表达式,这也可以在栈中读取。
4、二叉树的实现 Java描述
public class BinaryTree<T extends Comparable<? super T>> {
private BinaryNode<T> root1;
/**
* 节点类
*
* @param <T>
*/
private static class BinaryNode<T> {
// 数据存放区
private T element;
// 左子树
private BinaryNode<T> left;
// 右子树
private BinaryNode<T> right;
BinaryNode(T t) {
this(t, null, null);
}
public BinaryNode(T t, BinaryNode<T> lt, BinaryNode<T> rt) {
element = t;
left = lt;
right = rt;
}
}
----------
------------------