布谷鸟散列
1、定义
1.1 描述
假设有N个项,我们维护两个分别超过半空的表,且有独立的散列函数,可以把每个项分配到每个表中的一个位置,布谷鸟散列保持不变的是一个项总是会被存储在这两个位置之一。
-
维护2个超过半空的散列表
-
每个表有独立的散列函数
-
每个项都在2个表中有对应位置
1.2 图解
图解
-
图解说明:
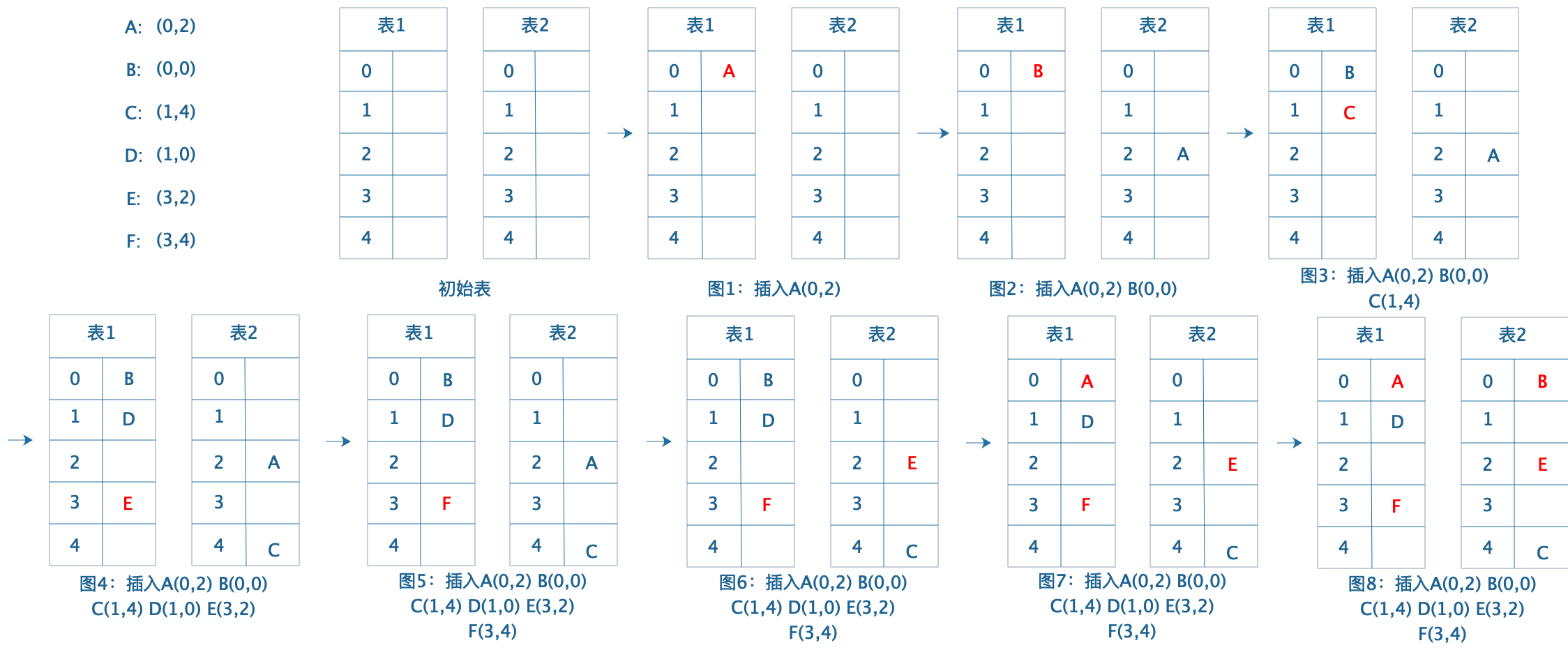
我们的初始状态为2张表,分别由2个散列函数维护,现在我们有ABCDEF 共6个元素,每个元素在2张表中均有散列位置(例如A在表1中的散列位置为0,在表2中的散列位置为2),开始插入
-
图1:插入A,先寻找在表1点散列位置0,插入到位置0;
-
图2:插入B,先寻找在表1点散列位置0,插入到位置0,但是位置0已经有A存在,后插入优先原则,B将A从表1点位置0挤走,A进入备选位置,插入表2点位置2;
-
图3:插入C,在表1点位置1插入C,没有冲突;
-
图4:插入D,在表1的位置为1,产生冲突,将C挤走,C插入表2位置4;
插入E,在表1点位置3;
-
图5:插入F,在表1点位置3,产生冲突,将E挤走;
-
图6:E被挤到表2位置2,产生冲突,将A挤走;
-
图7:A被挤到表1位置0,产生冲突,将B挤走;
-
图8:B被挤到表2位置0,没有冲突,最终状态确定。
-
2、循环
在上述图解中,我们看到在进行元素插入时,我们总是优先插入当前插入的元素,若产生冲突,则将原位置的元素挤走,如此类推,知道所有元素没有冲突的插入。但是,这种模式有个很明显的问题,就是如果散列值不好,则很容易发生循环,即插入导致永远的在挤走冲突元素,永远都在冲突状态。例如:在上述图解中插入G(1,2)。就会产生循环。
2.1 循环概率
有研究表明,如果表的装填因子小于0.5,循环的概率非常低。
3、扩展
如果在2张表的基础上,建立更多的表用来散列,比如3表分散,4表分散。虽然这样做增加了查找的开销,但也大幅度增加了空间的利用。因为每张表都会很小。
4、优势
布谷鸟散列的优势:
- 最坏情况下常数级的查找和删除时间。
- 避免了懒惰删除和额外的数据以及并行化的可能性。
5、代码实现
https://github.com/dhcao/dataStructuresAndAlgorithm/blob/master/src/chapterFive/CuckooHashTable.java