https://blog.csdn.net/yuhk231/article/details/80810427
皮尔逊相关系数实现相似K线及其性能优化
概念介绍
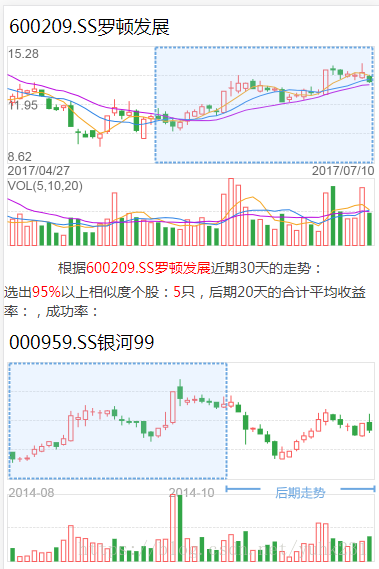
相似K线是验证“历史总会重演”的一个经典产品,目前许多炒股软件都开始陆陆续续提供相似K线功能。如下图是某产品的相似K线效果图:
投资者可以根据相似K线展示的结果来观察个股可能的未来走势,从而对投资起到一定的指导作用。
本文就将简要介绍如何实现相似K线的计算,并讨论实现过程中的一些难点细节。
计算及实现
相似K线的实现主要分为两大部分,第一部分是相似度匹配计算;第二部分是排名筛选。
相似度匹配
进行相似度匹配时我们使用“皮尔逊相关系数”(Pearson product-moment correlation coefficient)来进行相关度验证。详细的“皮尔逊相关系数”的推导及演算可从网上找到相关资料。本文我们直接使用结论公式:
P X , Y = ∑ X Y − ∑ X ∑ Y N ( ∑ X 2 − ( ∑ X ) 2 N ) ( ∑ Y 2 − ( ∑ Y ) 2 N ) P_{X,Y}=frac{sum{XY}-frac{sum{X}sum{Y}}{N}}{sqrt{(sum{X^2}-frac{(sum{X})^2}{N})(sum{Y^2}-frac{(sum{Y})^2}{N})}}PX,Y=(∑X2−N(∑X)2)(∑Y2−N(∑Y)2)
/*
* Pearson皮尔森相关系数计算
* (∑XY-∑X*∑Y/N)/(Math.sqrt((∑X^2-(∑X)^2/N)*((∑Y^2-(∑Y)^2/N)))
*/
pearsonManager=(function(){
var compare,calcCov,calcDenominator;
/*
* 协方差计算
* ∑XY-∑X*∑Y/N
* @param {array} source 源K线数据
* @param {array} data 对比的K线数据,data.length=source.length
* @param {string} field 参数
*/
calcCov=function(source,data,field){
var i,l,mulE,sourceE,dataE;
mulE=0;
sourceE=0;
dataE=0;
for(i=0,l=source.length;i<l;i++){
mulE+=source[i][field]*data[i][field];
sourceE+=source[i][field];
dataE+=data[i][field];
}
return mulE-sourceE*dataE/l;
};
/*
* 皮尔森分母计算
* Math.sqrt((∑X^2-(∑X)^2/N)*((∑Y^2-(∑Y)^2/N))
* @param {array} source 源K线数据
* @param {array} data 对比的K线数据,data.length=source.length
* @param {string} field 参数
*/
calcDenominator=function(source,data,field){
var i,l,sourceSquareAdd,sourceAdd,dataSquareAdd,dataAdd;
sourceSquareAdd=0;
sourceAdd=0;
dataSquareAdd=0;
dataAdd=0;
for(i=0,l=source.length;i<l;i++){
sourceSquareAdd+=source[i][field]*source[i][field];
sourceAdd+=source[i][field];
dataSquareAdd+=data[i][field]*data[i][field];
dataAdd+=data[i][field];
}
return Math.sqrt((sourceSquareAdd-sourceAdd*sourceAdd/l)*(dataSquareAdd-dataAdd*dataAdd/l));
};
/*
* 对比两组输入数据的相似度
* @param {array} source 源K线数据
* @param {array} data 对比的K线数据,data.length=source.length
* @param {string} field 参数
*/
compare=function(source,data,field){
var numerator,denominator;
if(source.length!=data.length){
console.error("length is different!");
return ;
}
numerator=calcCov(source,data,field);
denominator=calcDenominator(source,data,field);
return numerator/denominator;
};
return {
compare:compare
};
})();
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
我们可以试着用以下数据来计算相关系数:
var testSource,testData;
testSource=[{value:1},{value:2},{value:3}];
testData=[{value:3},{value:2},{value:1}];
console.log(pearsonManager.compare(testSource,testData,"value"));
- 1
- 2
- 3
- 4
输出的结果为-1,目标数据呈完全负相关。
由此,我们就得到了对比相似度的方法。下一步我们将要从全市场历史数据中找出相关度最高的相似K线数据。
排名筛选优化
注意!
后文代码摘录进本文时已经剔除了业务层代码,仅展示核心计算逻辑。以下数据结果均为2017-08-28运行得到。并且以下计算仅为单支股票的历史数据遍历,没有完整的运行全市场的数据,遍历全市场的时间消耗可以通过单支股票的运行时间估算得到。在下文特例中,就是对比600570.SS最新30天的数据和600571.SS历史所有数据的相似度。
遍历计算
最简单的实现方法就是全市场计算,蛮力遍历,将得到的所有结果进行排序,最终得到相似K线:
/*
* 遍历计算
* 2个属性20ms,最高相似度0.9505
* 600570:600571{position: 20130415, similar: 0.9505145006910938}
*/
compareSimilarKViolent=function(code,period,data){
var i,l,compareData,startTime,result;
compareData=[];
result=[];
for(i=0,l=data.length;i<l;i++){
compareData[i]={
date:data[i][0],
open:data[i][1],
high:data[i][2],
low:data[i][3],
close:data[i][4],
amount:data[i][5]
};
}
startTime=new Date().getTime();
for(i=0,l=data.length-31;i<l;i++){
result[i]={
start:data[i][0],
end:data[i+compareCount][0],
similar:calcSimilar(sourceData,compareData.slice(i,i+compareCount))
};
}
result.sort(function(a,b){
return b.similar- a.similar;
});
result=result.slice(0,10);
console.log(result);
console.log("calc cost:",new Date().getTime()-startTime);
};
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
这种算法实现简单,并且得到的结果一定是相似度最高的数据。但是这种算法需要将所有数据完整遍历计算,并且过程中需要保存下每个数据的计算结果,最终排序后得到最相似的数据,从时间和空间角度来看性能极差。
遍历计算优化
于是我们想到可以对排序进行优化:因为不会出现漏算的情况,我们在计算过程中只保存当前最高相似度数据的值,这样就节省了排序数组的空间和最后排序的时间:
/*
* 遍历计算,取最大值算法优化,无需存储无意义的全部数据
* 2个属性17ms,最高相似度0.9505
* 600570:600571{position: 20130415, similar: 0.9505145006910938}
*/
compareSimilarKViolentOptimize=function(code,period,data){
var i,l,compareData,startTime,result,similarValue;
compareData=[];
for(i=0,l=data.length;i<l;i++){
compareData[i]={
date:data[i][0],
open:data[i][1],
high:data[i][2],
low:data[i][3],
close:data[i][4],
amount:data[i][5]
};
}
startTime=new Date().getTime();
i=0;
result={
start:data[i][0],
end:data[i+compareCount][0],
similar:calcSimilar(sourceData,compareData.slice(i,i+compareCount))
};
for(i=1,l=data.length-31;i<l;i++){
similarValue=calcSimilar(sourceData,compareData.slice(i,i+compareCount));
if(result.similar<similarValue){
result={
start:data[i][0],
end:data[i+compareCount][0],
similar:similarValue
};
}
}
console.log(result);
console.log("calc cost:",new Date().getTime()-startTime);
};
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
可以看到,运行时间几乎得到了15%的性能提升。并且新的算法在空间上也更优。
分治算法
虽然经过了优化,但是我们仍然无法避免大规模的数据运算,这种缺陷在进行全市场数据运算时将会暴露的更加凸显。介于此,我们提出一种可行的优化算法:引入分治思想。对于本文中的特定案例,我们计算600570最新30天的数据,也就是说每次循环,皮尔逊公式将计算两组长度为30的数组数据的相似度。为了降低计算量,我们从数组中选取几个特征数据,例如选取数组头、数组中、数组尾三个数据来计算相关度,替代每次都完整计算整个数据的相似度,在粗略计算后选取相似度排名前几位,然后对这前几位数据索引再进行完整计算:
/*
* 分治计算
* 2个属性4.3ms,divide=3最高相似度0.9501(cut越大近似度越高)
* cut*compareCount+totalLength*divide=totalLength*compareCount;
* 当compareCount=30,totalLength=1404,divide=3时,cut=1263
*/
compareSimilarKCut=function(code,period,data){
var i,j,l,compareData,startTime,result,cut,position,
divide,divideStep,divideIndex,tempSource,tempCompare;
compareData=[];
result=[];
for(i=0,l=data.length;i<l;i++){
compareData[i]={
date:data[i][0],
open:data[i][1],
high:data[i][2],
low:data[i][3],
close:data[i][4],
amount:data[i][5]
};
}
startTime=new Date().getTime();
cut=100;
divide=3;
divideIndex=[0];
divideStep=compareCount/(divide-1);
tempSource=[sourceData[divideIndex[0]]];
for(i=1;i<divide-1;i++){
divideIndex[i]=divideStep*i;
tempSource[i]=sourceData[divideIndex[i]];
}
divideIndex[i]=compareCount-1;
tempSource[i]=sourceData[divideIndex[i]];
for(i=0,l=data.length-1-compareCount;i<l;i++){
tempCompare=[];
for(j in divideIndex){
tempCompare.push(compareData[i+divideIndex[j]]);
}
result[i]={
start:i,
similar:calcSimilar(tempSource,tempCompare)
}
}
result.sort(function(a,b){
return b.similar- a.similar;
});
result=result.slice(0,cut);
for(i=0,l=result.length;i<l;i++){
position=result[i].start;
result[i]={
start:data[position][0],
end:data[position+compareCount][0],
similar:calcSimilar(sourceData,compareData.slice(position,position+compareCount))
}
}
result.sort(function(a,b){
return b.similar- a.similar;
});
console.log(result);
console.log("calc cost:",new Date().getTime()-startTime);
};
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
对于这种算法,有一个性能公式可以参考(以下变量名和程序中相同):
c u t ∗ c o m p a r e C o u n t + t o t a l L e n g t h ∗ d i v i d e = t o t a l L e n g t h ∗ c o m p a r e C o u n t cut*compareCount+totalLength*divide=totalLength*compareCountcut∗compareCount+totalLength∗divide=totalLength∗compareCount
公式中,cut表示粗略计算后截取前多少名进行精确计算(本例中取值为100),compareCount表示整个对比数据的长度(本例中就是30),totalLength表示历史数据的长度(本例中600571历史数据长度为1404),divide表示特征数据个数(本例中用3个特征数代替30的完整数据)。对于这个公式,divide和cut是由开发人员主观定义的。divide越大,粗略计算的成本也就越高,当cut=compareCount时,这个算法也就退化成第一种蛮力遍历算法;cut越大,最后的精确计算成本也越高,但是注意cut不能太小,因为粗略计算过程中实际上是个贪婪计算过程,可能会遗失全局最优解而得到局部最优解。另一点要说明的是,该算法计算过程中也必须保存一个数据长度的相似度数组来进行最后的排序,因此空间消耗和第一种蛮力遍历算法一样大(可以通过维护一个长度为cut的降序数组保存相似度前几位的数据,来进行小幅度的优化,大约提升15%的性能)。
动态规划算法
对于这个问题场景,有不有存在一种既节省空间有节省时间的算法存在呢?答案就是动态规划算法。
动态规划算法的详细介绍可以从网上找到相关资料,本文对于概念只做简单介绍。简单来说,动态规划就是指当前计算可以利用前一次的计算结果。对于皮尔逊公式,我们可以将中间计算过程存储下来,并在数据遍历的时候只变化头尾数据,这样就不需要保存所有相似度计算结果再到最后进行排序,而只需要维护一个长度为compareCount(本例中即30)的中间计算状态数组,在空间上解决了问题;由于每一步计算基于前一步计算的结果,因此除了第一步需要完整计算一个compareCount(本例中即30)的皮尔逊系数,后续每一次循环都只进行很少的“头尾替换”计算,因此理论上该算法在时间上的性能也是极优的。对于这个算法,我们也会得到全局最优解的精确解。程序代码如下:
/*
* 动态规划
* 2个属性4.2ms,最高相似度0.9505
*/
compareSimilarKDynamic=function(code,period,data){
var i,l,compareData,startTime,result,similarValue,atomOpen,atomClose,
tempCompare,mulOpen,mulClose;
var calcPearson,calcAtom,calcMulAdd,dynamic;
/*
* 原子公式计算皮尔逊相关系数
* 返回[∑X,∑Y,∑X^2,∑Y^2,N]
* @param {array} source 源K线数据
* @param {array} data 对比的K线数据,data.length=source.length
* @param {string} field 参数
*/
calcAtom=function(source,data,field){
var i,l,sourceSquareAdd,sourceAdd,dataSquareAdd,dataAdd;
sourceSquareAdd=0;
sourceAdd=0;
dataSquareAdd=0;
dataAdd=0;
for(i=0,l=source.length;i<l;i++){
sourceAdd+=source[i][field];
dataAdd+=data[i][field];
sourceSquareAdd+=source[i][field]*source[i][field];
dataSquareAdd+=data[i][field]*data[i][field];
}
return [sourceAdd,dataAdd,sourceSquareAdd,dataSquareAdd,l];
};
/*
* 计算累乘
* @param {array} source 源K线数据
* @param {array} data 对比的K线数据,data.length=source.length
* @param {string} field 参数
*/
calcMulAdd=function(source,data,field){
var i,l,mulAdd;
mulAdd=0;
for(i=0,l=source.length;i<l;i++){
mulAdd+=source[i][field]*data[i][field];
}
return mulAdd;
};
/*
* 计算皮尔逊值
* (∑XY-∑X*∑Y/N)/(Math.sqrt((∑X^2-(∑X)^2/N)*((∑Y^2-(∑Y)^2/N)))
*/
calcPearson=function(mul,data){
return (mul-data[0]*data[1]/data[4])/(Math.sqrt((data[2]-data[0]*data[0]/data[4])*(data[3]-data[1]*data[1]/data[4])));
};
/*
* 动态规划分步变化
*/
dynamic=function(atom,field){
var value;
value=compareData[i+compareCount-1];
atom[1]=atom[1]-compareData[i-1][field]+value[field];
atom[3]=atom[3]-compareData[i-1][field]*compareData[i-1][field]+value[field]*value[field];
return atom;
};
compareData=[];
for(i=0,l=data.length;i<l;i++){
compareData[i]={
date:data[i][0],
open:data[i][1],
high:data[i][2],
low:data[i][3],
close:data[i][4],
amount:data[i][5]
};
}
startTime=new Date().getTime();
i=0;
tempCompare=compareData.slice(i,i+compareCount);
mulOpen=calcMulAdd(sourceData,tempCompare,"open");
mulClose=calcMulAdd(sourceData,tempCompare,"close");
atomOpen=calcAtom(sourceData,tempCompare,"open");
atomClose=calcAtom(sourceData,tempCompare,"close");
similarValue=0.5*calcPearson(mulOpen,atomOpen)+0.5*calcPearson(mulClose,atomClose);
result={
start:data[i][0],
end:data[i+compareCount][0],
similar:similarValue
};
for(i=1,l=data.length-31;i<l;i++){
tempCompare=compareData.slice(i,i+compareCount);
mulOpen=calcMulAdd(sourceData,tempCompare,"open");
mulClose=calcMulAdd(sourceData,tempCompare,"close");
atomOpen=dynamic(atomOpen,"open");
atomClose=dynamic(atomClose,"close");
similarValue=0.5*calcPearson(mulOpen,atomOpen)+0.5*calcPearson(mulClose,atomClose);
if(result.similar<similarValue){
result={
start:data[i][0],
end:data[i+compareCount][0],
similar:similarValue
};
}
}
console.log(result);
console.log("calc cost:",new Date().getTime()-startTime);
};
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
该算法唯一的缺点就是实现复杂。本身将简单的循环计算修改成动态规划循环就是一个不小的挑战;其次,在这个问题场景下,我们还需要修改对皮尔逊公式的实现,来保存中间过程,可以看到代码中我们使用calcAtom和calcPearson重写了皮尔逊公式的代码实现。
代码调优
对于生产级高TPS场景,在此本文再给出一种经过“代码调优”之后的程序实现。算法本身是基于动态规划(算法四),但是具体的实现形式从“面向对象”转向了“面向过程”。在下面这套代码中,我们对冗余的循环进行合并、去除多余的方法栈调用、去除了多余的内存分配(Array.slice),最终得到了比蛮力遍历性能提升113倍(比算法四性能提升22倍)的计算程序。使用下面的程序进行全市场遍历计算,单线程只需要30分钟。
/*
* 动态规划
* 内存优化(数组maloc),去除方法栈开销(面向过程)
* 2个属性0.17ms,最高相似度0.9505
*/
compareSimilarKDynamicOptimize=function(code,period,data){
var i,l,compareData,startTime,result,similarValue,atomOpen,atomClose,
j,k,mulOpen,mulClose,sourceSquareAdd,sourceAdd,dataSquareAdd,dataAdd,
m;
compareData=[];
for(i=0,l=data.length;i<l;i++){
compareData[i]={
date:data[i][0],
open:data[i][1],
high:data[i][2],
low:data[i][3],
close:data[i][4],
amount:data[i][5]
};
}
startTime=new Date().getTime();
//tempCompare=compareData.slice(i,i+compareCount);
/*
* mulOpen=calcMulAdd(sourceData,tempCompare,"open");
* mulClose=calcMulAdd(sourceData,tempCompare,"close");
*/
i=0;
mulOpen=0;
mulClose=0;
for(l=i+compareCount;i<l;i++){
mulOpen+=sourceData[i].open*compareData[i].open;
mulClose+=sourceData[i].close*compareData[i].close;
}
/*
* atomOpen=calcAtom(sourceData,tempCompare,"open");
* atomClose=calcAtom(sourceData,tempCompare,"close");
*/
sourceSquareAdd=0;
sourceAdd=0;
dataSquareAdd=0;
dataAdd=0;
for(i=0;i<l;i++){
sourceAdd+=sourceData[i].open;
dataAdd+=compareData[i].open;
sourceSquareAdd+=sourceData[i].open*sourceData[i].open;
dataSquareAdd+=compareData[i].open*compareData[i].open;
}
atomOpen=[sourceAdd,dataAdd,sourceSquareAdd,dataSquareAdd,l];
sourceSquareAdd=0;
sourceAdd=0;
dataSquareAdd=0;
dataAdd=0;
for(i=0;i<l;i++){
sourceAdd+=sourceData[i].close;
dataAdd+=compareData[i].close;
sourceSquareAdd+=sourceData[i].close*sourceData[i].close;
dataSquareAdd+=compareData[i].close*compareData[i].close;
}
atomClose=[sourceAdd,dataAdd,sourceSquareAdd,dataSquareAdd,l];
/*
* similarValue=0.5*calcPearson(mulOpen,atomOpen)+0.5*calcPearson(mulClose,atomClose);
*/
similarValue=0.5*(mulOpen-atomOpen[0]*atomOpen[1]/atomOpen[4])/(Math.sqrt((atomOpen[2]-atomOpen[0]*atomOpen[0]/atomOpen[4])*(atomOpen[3]-atomOpen[1]*atomOpen[1]/atomOpen[4])))+0.5*(mulClose-atomClose[0]*atomClose[1]/atomClose[4])/(Math.sqrt((atomClose[2]-atomClose[0]*atomClose[0]/atomClose[4])*(atomClose[3]-atomClose[1]*atomClose[1]/atomClose[4])));
result={
start:data[0][0],
end:data[compareCount][0],
similar:similarValue
};
for(i=1,l=data.length-31;i<l;i++){
//tempCompare=compareData.slice(i,i+compareCount);
/*
* mulOpen=calcMulAdd(sourceData,tempCompare,"open");
* mulClose=calcMulAdd(sourceData,tempCompare,"close");
*/
mulOpen=0;
mulClose=0;
for(j=0,k=i,m=i+compareCount;k<m;k++,j++){
mulOpen+=sourceData[j].open*compareData[k].open;
mulClose+=sourceData[j].close*compareData[k].close;
}
/*
* atomOpen=dynamic(atomOpen,"open");
* atomClose=dynamic(atomClose,"close");
*/
var value;
value=compareData[i+compareCount-1];
atomOpen[1]=atomOpen[1]-compareData[i-1].open+value.open;
atomOpen[3]=atomOpen[3]-compareData[i-1].open*compareData[i-1].open+value.open*value.open;
atomClose[1]=atomClose[1]-compareData[i-1].close+value.close;
atomClose[3]=atomClose[3]-compareData[i-1].close*compareData[i-1].close+value.close*value.close;
/*
* similarValue=0.5*calcPearson(mulOpen,atomOpen)+0.5*calcPearson(mulClose,atomClose);
*/
similarValue=0.5*(mulOpen-atomOpen[0]*atomOpen[1]/atomOpen[4])/(Math.sqrt((atomOpen[2]-atomOpen[0]*atomOpen[0]/atomOpen[4])*(atomOpen[3]-atomOpen[1]*atomOpen[1]/atomOpen[4])))+0.5*(mulClose-atomClose[0]*atomClose[1]/atomClose[4])/(Math.sqrt((atomClose[2]-atomClose[0]*atomClose[0]/atomClose[4])*(atomClose[3]-atomClose[1]*atomClose[1]/atomClose[4])));
if(result.similar<similarValue){
result={
start:data[i][0],
end:data[i+compareCount][0],
similar:similarValue
};
}
}
//console.log(result);
//console.log("calc cost:",new Date().getTime()-startTime);
return new Date().getTime()-startTime;
};
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
总结
基于上述讨论和测试(不考虑程序示例五,因为程序五不是一种算法设计技术,而是一种代码调优技术),得到以下算法性能结果:
时间消耗:算法三<算法四<算法二<算法一
空间消耗:算法二<算法四<算法三=算法一
实现难度:算法一<算法二<算法三<算法四
相似K线对于金融投资的实战应用作用
其实对于大部分数据段,在任何一支上市五六年以上的股票历史数据上都可以找到相似度大于0.9的数据段,我们在许多产品上看到的排名前几位的相似K线也仅仅只是沧海一粟,对应的后期走势也不可能代表所有数据情况,所以笔者在此对相似K线的有效性仍然持怀疑态度。什么意思呢,对于一段数据,查找出的一个相似K线提示未来价格上升,而另一个相似K线则提示未来价格下跌,那投资者如何判断?并且这种分化走势是一定存在的,如果我们在某个产品上看到的相似K线显示未来100%上涨,那只是这个产品没有把数据算全而已。相似K线只能提供形态上的模拟近似,并不能完整的将当前个股和历史数据的金融条件(消息面、基本面等)完全匹配。