链接:https://www.zhihu.com/question/26435474/answer/115096370
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
- 最小作用量原理的提出
- 极值思想的产生
热力学系统平衡时,熵值最大;水珠尽可能的保持球形,在失重的空中,水珠可以保持完美的球形,因为相同体积的物体,球形表面积最小, 等等。
以上种种现象表明,造物主似乎是个精明的经济学家,他总是尽心设计物理定律使得“成本”最小。很久以前,人们认为这些极值问题仅仅是一些物理定律的偶然结果,可是随着理论的发展,人们似乎慢慢认识到极值才是宇宙中最本质的定律。在今天,物理学家们已经找到了一种以统一的形式和精确的数学去描述这些极值问题的原理——最小作用量原理。
而人们从心理上也往往比较喜欢极值, 比如学生都想得最高分;买电脑要买性价
比最高的;上班坐公交要坐最省时间的;做生意要求利润要最高,等等。而最小作用量原理也正是人们在这样的社会背景下提出的,17 世纪末至18 世纪初,随着资本主义的发展,经济因素在人们的思想和行动上产生了很多影响。 人们总想让社会的生产效率达到最高,经济效益达到最好。
这使得很多哲学家将自然界的极值与人类社会的极值联系起来,自然界的极值性和人类的经济理论,进而发展为自然界的经济原理。 致使很多大哲学家和科学家开始运用这一思想,寻求自然界的存在形式。 包括牛顿、莱布尼兹、欧拉等人,正是在这
样的时代背景下,促成了最小作用量原理的创立及其规范化。
- “作用量”的概念
就是我们无法定量的描述作用量,甚至,也没有对作用量有一个明确的认识和定义。
大多数人刚开始接触最小作用量原理时,也都有这样一个疑问,什么是“作用量”,
既然最小作用量原理在各个物理领域都可以运用,那么这个“作用量”又是怎样定义
的,怎样寻找的呢?
最初,作用量的提出完全来自于人们的猜测和实验验证。但随着最小作用量原理的发展,以及守恒律、对称性的理论研究,三者之间的关系也渐渐明朗起来, 1918 年,
E·诺特在题为“变分问题的不变量”论文中提出著名的“诺特定理”,至此,我们已经可以从理论上寻找作用量的数学形式,通过对称、守恒与最小作用三者之间的关系有效地写出正确的作用量函数,这种方法进而发展为规范场论。
那么人们最初是怎样认识作用量的呢?下面我们先看一个简单的例子:如下图所示: 一个落水者向岸边的人求救,假设恰好跨栏冠军刘翔在此时经过,
救人者刘翔此时往往有两个选择: 1、经过 A 点,选取最短路径,直奔落水者实施救援。 2、经过 B 点,首先迅速跑到离落水者较近的岸边,然后游泳到落水地点。
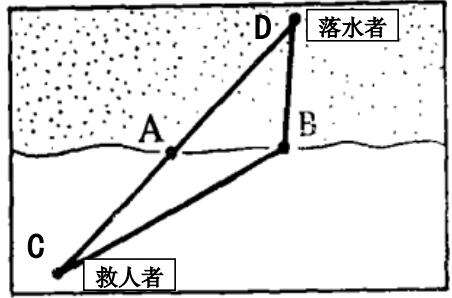
首先,我们要明确一个目的,就是要尽快的将人救出,也就是要求到达落水者地点的时间尽可能的短。在这里,如果说我们运用最小作用量原理来研究此问
题,这里的最小“作用量”就是“时间”。那么为什么不是最短的路程呢?难道最短路程不等于最短时间么?
在人们看来,救人肯定是要求时间最短,而不是路径最短,所以这里选取时间为作用量,而到达落水点的路径只有一条是时间最短的,对刘翔来说,其跑步速度肯定远大于游泳速度。所以,在陆地上奔跑更省时,刘翔尽可能的先跑到离落水者最近的岸边,再选择游泳,能更快的到达落水点。所以此时,时间是作用量,而选择直线的
最短距离,花费的时间反而更长。 也就是由时间最短原理,我们可以得出刘翔唯一的一条运动路径CBD。
这样,我们就得出了作用量的概念,并从以上例子中,我们由最小作用量原理得出了唯一的一条满足时间最短原理的路径。那么,联想到自然经济原理,如果自然界也存在这样的作用量,那么我们是否也能找到这样一个作用量,并计算出自然界中物体的运动路径呢?
- 自然界的最小作用量原理
我们容易类比,难道光也是选择了时间最短的运动路径么?其实,很早之前,古代科学家(如公元前 2 世纪的埃及人 Hero)就开始猜想光的传播遵从最短时间法则。最小作用量原理的第一个成功范例是 1650年法国数学家费马对光的传播原理作了一个概括性的叙述:光从空间一点 A 到另一点 B,光沿着所需的时间为极值的路径传播。但是,其折射的角度究竟是否对应着最短时间的路径,还要结合折射定律
以及光在介质中的速度公式进一步计算。折射定律早在 1620 年,就由荷兰科学家斯涅耳在实验的基础上得出了,又由笛卡尔在其《折射光学》中将其表述为:
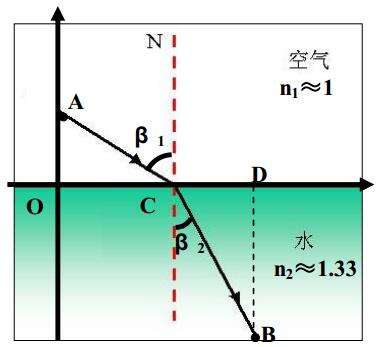
介质中的光速与折射率的关系是由惠更斯在其光的波动理论上给出的,即介质折射率之比等于光在这两种介质中的速度之比,这也使费马原理第一次得到了证明(具体方法不再列出)。
在以上的例子中,都是作用量取最小的情况,但是,在费马原理的表述中,并没有说光是沿着作用量取最小的路径传播的,而是用“极值” 代替了“最小”。这里涉及到了另一个问题,更准确的来讲,最小作用量原理,本就应该是极值原理。因为在上面我们就谈到了极值思想的产生,这里除了极小值还有极大值。进一步,学过数学中利用导数求极值的方法后就知道,利用函数的一阶导数等于零就能得到极值点。
而这个极值点还有可能既不是最大也不是最小,而是曲线的拐点。只是人们在研究此类问题时,遇到的情况更多的是涉及到最小值的,也就有了“最小作用量原理”。
- 变分法与分析力学
而把光的运动与力学中运动问题的首先进行比较的是伯努利( J.Bernoulli),他所提出的最速降线问题,是变分学发展的标志。变分研究的主要内容是泛函的极值,求泛函极值有关的问题通称为变分问题。 在其工作中,J.Bernoulli 试图将力学与光的运动联系起来,并由此建立折射率的力学理论,尽管他没有取得令人满意的结果,但这种思想为以后的 Hamilton 理论及其在其它不同领域的推广开辟了道路,由此而揭示了最小作用量原理与费马原理之间惊人的相似(提出费马原理时,最小作用量原理还没有得到更广泛的推广,后来最小作用量原理多用来描述动力学的原理)。
而后,莫培督最早于1744年提出了最小作用量原理,同年,欧拉发表了《寻求
具有某种极大或极小性质的曲线的方法》,该书为变分法的创立奠定了基础。而通过把最小作用量原理看作物理学基本原理并进而导出运动方程的杰出工作则主要归功于 Lagrange和Hamilton。在此之后亥姆霍兹等人对最小作用量原理与能量守恒之间的关系进行了进一步的研究。由此从最初的极值思想到最小作用量原理的引入,体现
了人们对于自然界本质规律的不断追求。
总之,分析力学的思路是根据最小作用量原理,运用变分法求解粒子的真实运动,拉格朗日力学给力学一种全新的研究思路与方法,也可以说最小用量原理在拉格朗日手中变为一种真正具有可计算的、形象化的物理思想,拉格朗日证明了物体系统的绝大多数结论都能从一个根本性的公式推导出来。这种追求普遍性、简单性、更深层物理意义的思想也正是科学源自于西方的根本原因。
- 对称、守恒与最小作用量
能求出运动方程,但是
幸运的是,对称与守恒有着一种深刻而神秘的联系,这一联系是19世纪的一位女数学家——艾米·诺特尔( Emmy Noether)发现的,后人将其命名为诺特尔定理:
作用量的每一种连续对称性都有一个守恒量与之对应。 通过三者之间的关系,可以进行互相推导,进而获得作用量的表达式。
时间或者空间的均匀性(对称性)具体的表示出来就是拉格朗日函数
然后我们就知道时间平移对称性对应于能量守恒,空间平移对称性对应于动量守恒,空间转动对称性对应于角动量守恒等。此外,还有很多对称、守恒关系,比如镜像对称与宇称守恒;规范场与粒子数守恒等等。这样,最小作用量原理、对称、守恒,就联系起来了:世界的运行满足最小作用量原理,作用最量的形式受对称性的约束,对称性又与某个守恒定律等价。这不是巧合,这是正是物理美的所在,也许总有一个最高的物理准则在统治着所有的物理规律,最小作用量原理的出现给了我们一个很好的启示。那么能否从最小作用量原理的角度来解读整个物理学,似乎还存在着一些困难。但是,在现代物理的发展过程中,最小作用量原理在各种物理学领域中更广泛的应用,使其变为最有可能解读一切物理规律的最高理论。
下面着重介绍作用量与量子力学的路径积分法的联系
- 作用量与量子力学的路径积分法
最小作用量原理还有一个神奇之处,就是费曼先生曾在他的“最小作用量原理”中做过的阐述:从微分的观点,粒子的运动是容易理解的。由于粒子受到力的作用,所以它的速度发生了变化,又由于粒子有速度,所以位置也改变了。换言之,每一时刻当粒子获得一加速度时仅仅知道在该时刻应该做什么。可是如果你讲粒子会做出决定以选取将能给出最小作用量的那条路线,这就完全是另一回事了。粒子怎么能知道周围其他的路线作用量来得要更大呢?或者说粒子会对不同路线的作用量进行比较吗?答案是肯定的! 就像光的衍射一样,当你在光的路径中放置一些障碍物,以至于光子不能实验出每一条路径时,光就无法算出该走哪一条路,也就出现了光的衍射,但这必须用量子力学的观点来解释。
量子力学中的路径积分法是由狄拉克于1933年在一篇“量子力学的拉格朗日函数”的文章中提出,之后由美国科学家理查德·费曼 Richard Feynman( 1918 年 5 月
11 日-1988 年 2 月 15 日)进一步发展而来。 费曼是一个天才,他对任何事情都不想当然的认为,总是以自己的方式去理解问题的本质,然后对自然界的行为得出一种新颖而深刻的解释,他讨厌死板的灌输式教育,认为学习就像是一种快乐的游戏,同时他自己又不失幽默感,有人评价他是一个天才,也是一个滑稽的演员。
那么什么是路径积分法呢?我们知道量子力学已经有了比较成熟的两种表示方
式,一是薛定谔的波动力学,一是狄拉克的矩阵力学。 传统的量子力学正是在它否定了粒子的轨道运动之后建立起了自己的完美的理论形式的,在波动力学里,粒子一会儿是波, 一会儿又成了粒子,虽然符合了实验现象,但这使人完全无法理解。 路径积分法可以说是量子力学的第三种表示方法,并且比前两种方法更具优越性。当然,路径积分法也并非完全是粒子形态的路径积分,而是场论形式的泛函积分方法。那么这种方法与“粒子会对不同路线的作用量进行比较”有什么关系呢?
当然首先,我们要了解什么是几率幅和几率,这是基于波的叠加现象引出的概念,那么按照费曼的路径积分法,粒子从点1到点2时,由于不确定性关系的影响,将不再只有一条和作用量有关的路径,而是具有无穷多可能的路径。
如图,一个粒子从时刻所处的点1出
发,在时刻到达点2的几率,等于一个几率幅的平方。
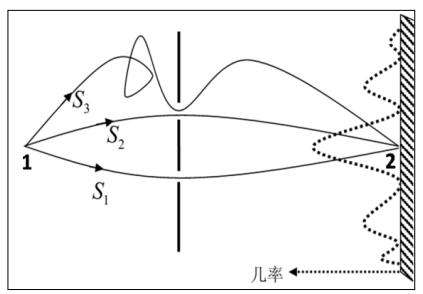
其中
它所描述的粒子运动具有这样的特征:几率幅与exp(iS/ℏ)相关, i
因此,在宏观世界中,由于ℏ近似为0,量子现象就过渡到了经典的运动轨迹,这就是最小作用量原理与量子力学的关系,
这与光学中的惠更斯原理相似,不同的是路径积分法中几率幅的大小都是相等的,而惠更斯原理中的振幅大小是与距离相关的。
可以说,路径积分法中“量子力学的几率概念并没有改变” ,在《量子力学与路径积分》这本著作中,费曼开门见山地指出: “所改变了的,并且根本地改变了的,是计算几率的方法。” 但对于几率幅究竟是怎么一回事,就无人知晓了,对此费曼发出感叹“几率幅几近不可思议” 。
- 对最小作用量原理的讨论
最小作用量原理的形成历史是曲折的,给予
从最小作用量原理出发,在时问均匀的前提下可以得到能量守恒定律。 若时间不均匀,能量守恒定律的成立问题仍处于研究之中,这种情况在广义相对论中尤为突出。
在广义相对论中, 时空弯曲、时间非均匀、引力能无法局域化, 广义相对论中能量守恒问题至今还未得到解决。 作用量S或许比能量概念更为重要。 能量反映了各种运动之间相互转化的共同量度,作用量则反映各种运动过程必须满足的共同性质,作用量的量纲是[能量·时间],是能量与时间的统一。 为此,我们可以认为能量仅反映了作用量中的一部分联系。
在量子力学中,有一个作用量常数(即普朗克常数)
然而,尽管人们做出了艰苦努力,但仍未从最小作用量原理满意地推导出热力学定律。 其原因可能是,热力学是研究大量微观粒子组成的宏观系统,存在热效应。热
力学过程是不可逆过程,存在耗散因素,时间具有不对称性。正如普朗克断定,作为
建立统一的世界物理图景之基础的最小作用量原理,是所有可逆过程的普遍原理。 本世纪60年代以来,非线性科学(如混沌学)成为举世瞩目的科学热点。混沌学揭示出系统固有地存在内在随机性,它给牛顿力学又加以新的限制,事实上牛顿力学对多体问题无从下手。 如此看来,最小作用量原理在非线性科学中将会受到限制。
爱因斯坦指出,一切科学发现的伟大目标在于“寻找一个能把观察到的事实联系在一起的思想体系,它将具有更大可能的简单性。”最小作用量原理不仅几乎把已知的事实,而且也将未知的事实纳入到一个思想体系中,其简单、优美,其具有高度的抽象性,又不失各种形象化的案例,在物理规律总又具有高度的统一性,最小作用量原理无疑已成为物理学的最高理论。
参考资料:最小作用量原理及其应用—秦伟