zoukankan html css js c++ java

HDU 1045

题目链接：http://acm.split.hdu.edu.cn/showproblem.php?pid=1045

Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)

Problem Description

Suppose that we have a square city with straight streets. A map of a city is a square board with n rows and n columns, each representing a street or a piece of wall.

A blockhouse is a small castle that has four openings through which to shoot. The four openings are facing North, East, South, and West, respectively. There will be one machine gun shooting through each opening.

Here we assume that a bullet is so powerful that it can run across any distance and destroy a blockhouse on its way. On the other hand, a wall is so strongly built that can stop the bullets.

The goal is to place as many blockhouses in a city as possible so that no two can destroy each other. A configuration of blockhouses is legal provided that no two blockhouses are on the same horizontal row or vertical column in a map unless there is at least one wall separating them. In this problem we will consider small square cities (at most 4x4) that contain walls through which bullets cannot run through.

The following image shows five pictures of the same board. The first picture is the empty board, the second and third pictures show legal configurations, and the fourth and fifth pictures show illegal configurations. For this board, the maximum number of blockhouses in a legal configuration is 5; the second picture shows one way to do it, but there are several other ways.

Your task is to write a program that, given a description of a map, calculates the maximum number of blockhouses that can be placed in the city in a legal configuration.

Input

The input file contains one or more map descriptions, followed by a line containing the number 0 that signals the end of the file. Each map description begins with a line containing a positive integer n that is the size of the city; n will be at most 4. The next n lines each describe one row of the map, with a '.' indicating an open space and an uppercase 'X' indicating a wall. There are no spaces in the input file.

Output

For each test case, output one line containing the maximum number of blockhouses that can be placed in the city in a legal configuration.

Sample Input

.X..

....

XX..

....

.X.

X.X

.X.

...

.XX

....

Sample Output

题意：

给一个N*N的方阵，“.”代表空地，“X”代表有一堵墙，现要求在空地上放置碉堡，并且满足同一条线上的碉堡间必须有一堵墙挡着，求最多能放置的碉堡数；

题解：

方法①

由于N<=4，所以放置碉堡情况最多不会超过2^16=65536，可以直接用DFS去暴力枚举每一个方格上是否放置碉堡；

AC代码：

 1 #include<cstdio>
 2 #include<algorithm>
 3 using namespace std;
 4 int n;
 5 char map[6][6];
 6 int ans;
 7 void dfs(int now,int num)
 8 {
 9     if(now==n*n+1)
10     {
11         ans=max(ans,num);
12         return;
13     }
14 
15     int row=(now-1)/n+1, col=(now-1)%n+1;
16 
17     if(map[row][col]=='X')
18     {
19         dfs(now+1,num);
20         return;
21     }
22 
23     bool ok=1;
24     for(int i=col-1;i>=1;i--)//向前遍历当前行
25     {
26         if(map[row][i]=='B')
27         {
28             ok=0;
29             break;
30         }
31         if(map[row][i]=='X') break;
32     }
33     for(int i=row-1;i>=1;i--)//向前遍历当前列
34     {
35         if(map[i][col]=='B')
36         {
37             ok=0;
38             break;
39         }
40         if(map[i][col]=='X') break;
41     }
42     if(ok)
43     {
44         map[row][col]='B';
45         dfs(now+1,num+1);
46         map[row][col]='.';
47     }
48     dfs(now+1,num);
49     return;
50 }
51 int main()
52 {
53     while(scanf("%d",&n) && n!=0)
54     {
55         for(int i=1;i<=n;i++) scanf("%s",map[i]+1);
56         ans=0;
57         dfs(1,0);
58         printf("%d
",ans);
59     }
60 }

View Code

方法②

用二分图最大匹配来做本题。

前置知识点：http://www.cnblogs.com/dilthey/p/7647630.html

建模：

我们对这个方阵的每一行，以方阵的边界或者一堵墙为端点，我们对每一个“行段”（从一端开始到一端结束）的方格组标记为一个顶点，全部放入L集；

例如：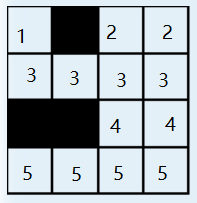

再对这个方阵的每一列，依然以方阵的边界或者一堵墙为端点，我们对每一个“列段”（从一端开始到一端结束）的方格组标记为一个顶点，全部放入R集；

例如：

那么，对应于方格内的每个格子，它们都有一个L集内的顶点编号，一个R集内的顶点编号，我们就建立一条连接两个这两个顶点的边；

then，根据匹配的要求，任意两条边都没有公共顶点，

即任意一个格子，都独占一个L集内的顶点，一个R集内的顶点，

即如果这里放了一个碉堡，那么它都独占了它所在的一个“行段”，一个“列段”，这就满足了任意两个碉堡间不会互相攻击；

那么，任意一种碉堡的放置方案，都对应一个「匹配」，我们找到最大匹配，就找到了放置碉堡最多的方案。

AC代码：

  1 #include<cstdio>
  2 #include<cstring>
  3 #include<vector>
  4 #define MAX 35
  5 using namespace std;
  6 //匈牙利算法 - st
  7 struct Edge{
  8     int u,v;
  9 };
 10 vector<Edge> E;
 11 vector<int> G[MAX];
 12 int lN,rN;
 13 int matching[MAX];
 14 int vis[MAX];
 15 void init(int l,int r)
 16 {
 17     E.clear();
 18     for(int i=l;i<=r;i++) G[i].clear();
 19 }
 20 void add_edge(int u,int v)
 21 {
 22     E.push_back((Edge){u,v});
 23     E.push_back((Edge){v,u});
 24     int _size=E.size();
 25     G[u].push_back(_size-2);
 26     G[v].push_back(_size-1);
 27 }
 28 bool dfs(int u)
 29 {
 30     for(int i=0,_size=G[u].size();i<_size;i++)
 31     {
 32         int v=E[G[u][i]].v;
 33         if (!vis[v])
 34         {
 35             vis[v]=1;
 36             if(!matching[v] || dfs(matching[v]))
 37             {
 38                 matching[v]=u;
 39                 matching[u]=v;
 40                 return true;
 41             }
 42         }
 43     }
 44     return false;
 45 }
 46 int hungarian()
 47 {
 48     int ret=0;
 49     memset(matching,0,sizeof(matching));
 50     for(int i=1;i<=lN;i++)
 51     {
 52         if(!matching[i])
 53         {
 54             memset(vis,0,sizeof(vis));
 55             if(dfs(i)) ret++;
 56         }
 57     }
 58     return ret;
 59 }
 60 //匈牙利算法 - ed
 61 int main()
 62 {
 63     int n;
 64     char mp[6][6];
 65     int row_id[5][5],col_id[5][5];
 66     while(scanf("%d",&n) && n!=0)
 67     {
 68         for(int i=1;i<=n;i++) scanf("%s",mp[i]+1);
 69 
 70         lN=0, rN=0;
 71         for(int i=1;i<=n;i++)//对“行段”进行编号
 72         {
 73             for(int j=1;j<=n;j++)
 74             {
 75                 if(mp[i][j]=='.')
 76                 {
 77                     if( j==1 || mp[i][j-1]=='X' ) row_id[i][j] = ++lN;
 78                     else row_id[i][j] = lN;
 79                 }
 80             }
 81         }
 82         for(int j=1;j<=n;j++)//对“列段”进行编号
 83         {
 84             for(int i=1;i<=n;i++)
 85             {
 86                 if(mp[i][j]=='.')
 87                 {
 88                     if( i==1 || mp[i-1][j]=='X' ) col_id[i][j] = lN + (++rN);
 89                     else col_id[i][j] = lN + rN;
 90                 }
 91             }
 92         }
 93 
 94         init(1,lN+rN);
 95         for(int i=1;i<=n;i++)//建边、建图
 96         {
 97             for(int j=1;j<=n;j++)
 98             {
 99                 if(mp[i][j]=='X') continue;
100                 add_edge(row_id[i][j],col_id[i][j]);
101             }
102         }
103 
104         printf("%d
",hungarian());
105     }
106 }

View Code

方法③

当然了，二分图最大匹配，也可以使用最大流来求解；

我们对二分图进行如此构建流网络：

建立超级源点s，超级汇点t；

对所有L集的点，连一条从s出发的边，容量为1；

对所有R集的点，连一条到达t的边，容量为1；

对原二分图本就存在的边，直接赋值容量=1，加入流网络；

最后求出最大流，即二分图的最大匹配。

AC代码：

  1 #include<cstdio>
  2 #include<cstring>
  3 #include<vector>
  4 #include<queue>
  5 #define MAX 35
  6 #define INF 0x3f3f3f3f
  7 using namespace std;
  8 struct Edge{
  9     int u,v,c,f;
 10 };
 11 struct Dinic
 12 {
 13     int s,t;
 14     vector<Edge> E;
 15     vector<int> G[MAX];
 16     bool vis[MAX];
 17     int lev[MAX];
 18     int cur[MAX];
 19     void init(int l,int r)
 20     {
 21         E.clear();
 22         for(int i=l;i<=r;i++) G[i].clear();
 23     }
 24     void addedge(int from,int to,int cap)
 25     {
 26         E.push_back((Edge){from,to,cap,0});
 27         E.push_back((Edge){to,from,0,0});
 28         int m=E.size();
 29         G[from].push_back(m-2);
 30         G[to].push_back(m-1);
 31     }
 32     bool bfs()
 33     {
 34         memset(vis,0,sizeof(vis));
 35         queue<int> q;
 36         q.push(s);
 37         lev[s]=0;
 38         vis[s]=1;
 39         while(!q.empty())
 40         {
 41             int now=q.front(); q.pop();
 42             for(int i=0,_size=G[now].size();i<_size;i++)
 43             {
 44                 Edge edge=E[G[now][i]];
 45                 int nex=edge.v;
 46                 if(!vis[nex] && edge.c>edge.f)
 47                 {
 48                     lev[nex]=lev[now]+1;
 49                     q.push(nex);
 50                     vis[nex]=1;
 51                 }
 52             }
 53         }
 54         return vis[t];
 55     }
 56     int dfs(int now,int aug)
 57     {
 58         if(now==t || aug==0) return aug;
 59         int flow=0,f;
 60         for(int& i=cur[now],_size=G[now].size();i<_size;i++)
 61         {
 62             Edge& edge=E[G[now][i]];
 63             int nex=edge.v;
 64             if(lev[now]+1 == lev[nex] && (f=dfs(nex,min(aug,edge.c-edge.f)))>0)
 65             {
 66                 edge.f+=f;
 67                 E[G[now][i]^1].f-=f;
 68                 flow+=f;
 69                 aug-=f;
 70                 if(!aug) break;
 71             }
 72         }
 73         return flow;
 74     }
 75     int maxflow()
 76     {
 77         int flow=0;
 78         while(bfs())
 79         {
 80             memset(cur,0,sizeof(cur));
 81             flow+=dfs(s,INF);
 82         }
 83         return flow;
 84     }
 85 }dinic;
 86 int main()
 87 {
 88     int n;
 89     char mp[6][6];
 90     int row_id[5][5],col_id[5][5];
 91     while(scanf("%d",&n) && n!=0)
 92     {
 93         for(int i=1;i<=n;i++) scanf("%s",mp[i]+1);
 94 
 95         int lN=0, rN=0;
 96         for(int i=1;i<=n;i++)//对“行段”进行编号
 97         {
 98             for(int j=1;j<=n;j++)
 99             {
100                 if(mp[i][j]=='.')
101                 {
102                     if( j==1 || mp[i][j-1]=='X' ) row_id[i][j] = ++lN;
103                     else row_id[i][j] = lN;
104                 }
105             }
106         }
107         for(int j=1;j<=n;j++)//对“列段”进行编号
108         {
109             for(int i=1;i<=n;i++)
110             {
111                 if(mp[i][j]=='.')
112                 {
113                     if( i==1 || mp[i-1][j]=='X' ) col_id[i][j] = lN + (++rN);
114                     else col_id[i][j] = lN + rN;
115                 }
116             }
117         }
118 
119         dinic.init(0,lN+rN+1);
120         dinic.s=0, dinic.t=lN+rN+1;
121         for(int i=1;i<=lN;i++) dinic.addedge(dinic.s,i,1);
122         for(int i=1;i<=rN;i++) dinic.addedge(i+lN,dinic.t,1);
123         for(int i=1;i<=n;i++)
124         {
125             for(int j=1;j<=n;j++)
126             {
127                 if(mp[i][j]=='X') continue;
128                 dinic.addedge(row_id[i][j],col_id[i][j],1);
129             }
130         }
131         printf("%d
",dinic.maxflow());
132     }
133 }

View Code

（当然，从复杂度上，就不难看出，用Dinic算法求二分图最大匹配比匈牙利算法慢。）

查看全文

相关阅读:
字符串基本操作
 条件、循环、函数定义练习
 turtle库基础练习
 Python基础练习
 AutoLayout 教程
 Mac上最佳的SVN管理工具：Cornerstone
图片上传关于压缩的问题
 关于单元测试的问题
 获取ios设备的当前IP地址
 关于项目使用ARC的管理方式

原文地址：https://www.cnblogs.com/dilthey/p/7647870.html