归并排序

开始时将表划分为大致相等的两段，然后对每个字表递归调用自身，直到划分为很多只含一个元素的子表，然后控制返回递归调用结构，算法将从两个递归调用中得到两个有序字段，合并为一个有序表。

比如初始数组：[24,13,26,1,2,27,38,15]

①分成了两个大小相等的子数组：[24,13,26,1]    [2,27,38,15]

②再划分成了四个大小相等的子数组：[24,13]   [26,1]    [2,27]    [38,15]

③此时，left < right 还是成立，再分：[24]   [13]   [26]    [1]    [2]     [27]    [38]   [15]

此时，有8个小数组，每个数组都可以视为有序的数组了！！！，每个数组中的left == right，从递归中返回(从19行--20行的代码中返回)，故开始执行合并(第21行)：

merge([24],[13]) 得到 [13,24]

merge([26],[1]) 得到[1,26]

.....

.....

最终得到 有序数组

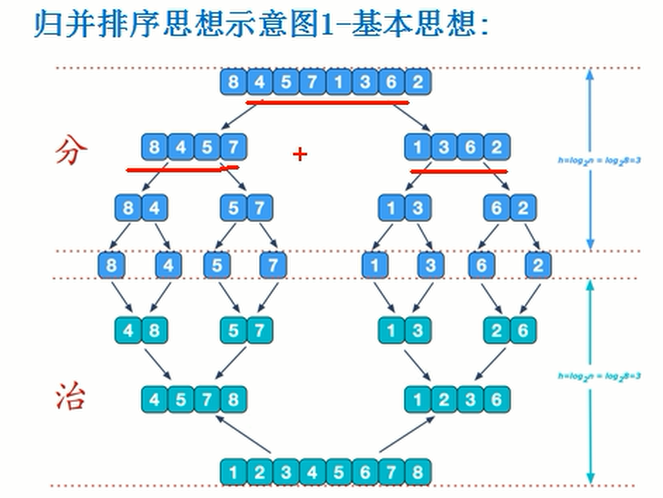
由上图可看出归并排序时间复杂度为n-1 ，为线性增长。

治的过程以倒数第二组为例：

 

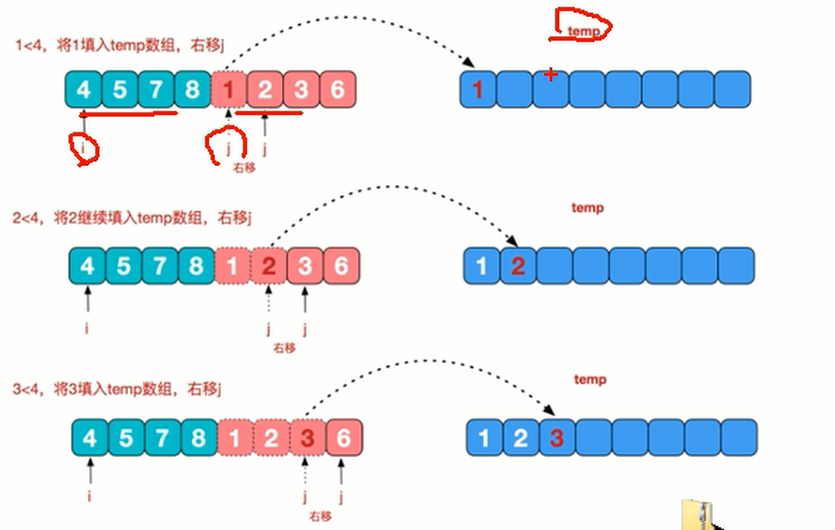
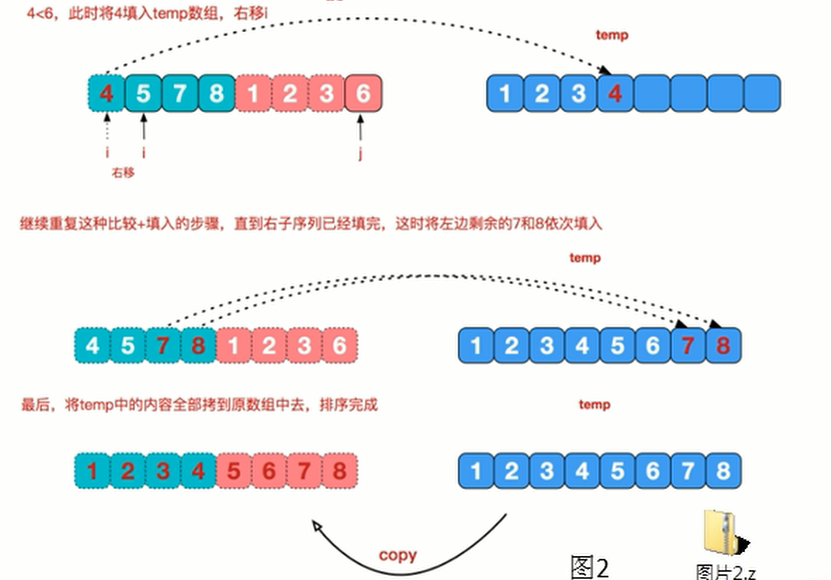
public class MergetSort {

    public static void main(String[] args) {
        //int arr[] = { 8, 4, 5, 7, 1, 3, 6, 2 }; //
        
        //测试快排的执行速度
        // 创建要给80000个的随机的数组
        int[] arr = new int[8000000];
        for (int i = 0; i < 8000000; i++) {
            arr[i] = (int) (Math.random() * 8000000); // 生成一个[0, 8000000) 数
        }
        System.out.println("排序前");
        Date data1 = new Date();
        SimpleDateFormat simpleDateFormat = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss");
        String date1Str = simpleDateFormat.format(data1);
        System.out.println("排序前的时间是=" + date1Str);
        
        int temp[] = new int[arr.length]; //归并排序需要一个额外空间
         mergeSort(arr, 0, arr.length - 1, temp);
         
         Date data2 = new Date();
        String date2Str = simpleDateFormat.format(data2);
        System.out.println("排序前的时间是=" + date2Str);
         
         //System.out.println("归并排序后=" + Arrays.toString(arr));
    }
    
    
    //分+合方法
    public static void mergeSort(int[] arr, int left, int right, int[] temp) {
        if(left < right) {
            int mid = (left + right) / 2; //中间索引
            //向左递归进行分解
            mergeSort(arr, left, mid, temp);
            //向右递归进行分解
            mergeSort(arr, mid + 1, right, temp);
            //合并
            merge(arr, left, mid, right, temp);
            
        }
    }
    
    //合并的方法
    /**
     * 
     * @param arr 排序的原始数组
     * @param left 左边有序序列的初始索引
     * @param mid 中间索引
     * @param right 右边索引
     * @param temp 做中转的数组
     */
    public static void merge(int[] arr, int left, int mid, int right, int[] temp) {
        
        int i = left; // 初始化i, 左边有序序列的初始索引
        int j = mid + 1; //初始化j, 右边有序序列的初始索引
        int t = 0; // 指向temp数组的当前索引
        
        //(一)
        //先把左右两边(有序)的数据按照规则填充到temp数组
        //直到左右两边的有序序列，有一边处理完毕为止
        while (i <= mid && j <= right) {//继续
            //如果左边的有序序列的当前元素，小于等于右边有序序列的当前元素
            //即将左边的当前元素，填充到 temp数组 
            //然后 t++, i++
            if(arr[i] <= arr[j]) {
                temp[t] = arr[i];
                t += 1;
                i += 1;
            } else { //反之,将右边有序序列的当前元素，填充到temp数组
                temp[t] = arr[j];
                t += 1;
                j += 1;
            }
        }
        
        //(二)
        //把有剩余数据的一边的数据依次全部填充到temp
        while( i <= mid) { //左边的有序序列还有剩余的元素，就全部填充到temp
            temp[t] = arr[i];
            t += 1;
            i += 1;    
        }
        
        while( j <= right) { //右边的有序序列还有剩余的元素，就全部填充到temp
            temp[t] = arr[j];
            t += 1;
            j += 1;    
        }
        
        
        //(三)
        //将temp数组的元素拷贝到arr
        //注意，并不是每次都拷贝所有
        t = 0;
        int tempLeft = left; // 
        //第一次合并 tempLeft = 0 , right = 1 //  tempLeft = 2  right = 3 // tL=0 ri=3
        //最后一次 tempLeft = 0  right = 7
        while(tempLeft <= right) { 
            arr[tempLeft] = temp[t];
            t += 1;
            tempLeft += 1;
        }
        
    }

}

 ------------------------------------------------------------------------------------------------

内容来自尚硅谷韩顺平视频教程