先从阿里机器学习算法岗网络笔试题说起:甲乙两人进行一个猜硬币的游戏。每个人有一个目标序列,由裁判来抛硬币。谁先得到裁判抛出的一串连续结果,谁赢。
甲的目标序列是正正正,乙的目标序列是反正正。那么如果裁判抛出了正正反正反正正....抛到第7个结果时乙胜,因为最后三个序列是“反正正”,而前面不存在甲的“正正正”序列。
问:甲的目标序列是????,乙的目标序列是????,求两人各自获胜的概率。
先说例子,正正正,反正正的概率。显然是1/8和7/8. 甲获胜的情况只有一种,就是三个连续的正,P = 1/8。为什么呢?因为,一旦裁判抛出一个“反”,结果就已经确定是乙胜了。所以甲要想获胜,只能从开头就是连着三个正。
那么对于一般题怎么做呢?
AC自动机 + 高斯消元。
你可以理解成 有限状态自动机+解方程。
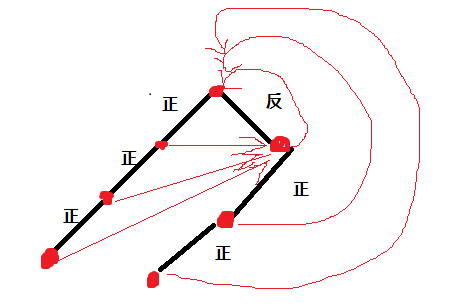
(不好意思 这个图有误,所有曲线指的不应该是根节点,而应该是根节点读入"反"后的右节点)
根节点是开始,每抛出一个硬币走一条边。谁先走到最底下的点就胜。
到底部的获胜概率就是从开始局面到底部的期望次数。(到所有终点的期望和是1,等价于所有人的获胜概率和是1)
这么转换后就能做了。每个结点的期望 = 它前驱结点的期望 的 加权平均值。
如果只有一条边出去,那么它的下一个结点的期望显然就等于它的期望。
自环也算进去,加权算。
那么就能对每个结点列方程,n元一次方程。常数项在哪里?
在根节点前虚拟一个结点,指向根结点。虚拟结点的期望是1。
然后就能高斯消元做了!
以上的过程其实是一个 马尔科夫 过程。
我们解决了自动机到终点的概率(获胜概率,也就是到终点的期望次数),我们类似可以解决自动机走到终点的期望步数。也就是裁判期望抛多少回硬币游戏能够结束?
同样是列方程。
xi表示到i结点需要走的期望步数, xi = 1+∑ (pj*xj), (xj 是xi 的前驱结点, pj是xj结点走到到xi结点的概率)???
xi表示从i结点走到终点的期望步数, xi = 1+∑ (pj*xj), (xj 是xi 的后继结点, pj是xj结点走到到xi结点的概率)
以上。
扩展
如果你和一个人玩游戏,是否存在一种情况,无论对方的序列是什么序列,你都能够构造出一个 等长 的序列,使你的获胜概率比对方大?
答案是:当序列长度 > 2时,你总能使自己获胜概率更大。
详见 matrix67
现场赛的题是投骰子,谁先投出自己的序列谁胜。求各自获胜概率。
正解:ac自动机+高斯消元。
有一个做n遍消元的解法:对每个人的目标点消元。具体就是设xi为i结点到目标点的概率,dp算出根结点的值就是从根节点到目标点的概率。做n次即可。
还有一种有误差的解法。矩阵快速幂。矩阵的n次幂表示从根节点走n步到各个点的概率。n足够大时,就能近似表示出到各个点的概率。可惜,精度还是不够,误差比较大。。。。
还是要贴一下AC代码的。
1 #include <bits/stdc++.h> 2 #define gg puts("gg"); 3 using namespace std; 4 const double eps = 1e-9; 5 const int N = 105; 6 int id(int c){ 7 return c-1; 8 } 9 struct Tire{ 10 int nex[N][6], fail[N], end[N]; 11 int root, L; 12 int newnode(){ 13 memset(nex[L], -1, sizeof(nex[L])); 14 end[L] = 0; 15 return L++; 16 } 17 void init(){ 18 L = 0; 19 root = newnode(); 20 } 21 void insert(int* s, int l, int k){ 22 int now = root; 23 for(int i = 0; i < l; i++){ 24 int p = id(s[i]); 25 if(nex[now][p] == -1) 26 nex[now][p] = newnode(); 27 now = nex[now][p]; 28 } 29 end[now] = k; 30 } 31 void build(){ 32 queue<int> Q; 33 fail[root] = root; 34 for(int i = 0; i < 6; i++){ 35 int& u = nex[root][i]; 36 if(u == -1) 37 u = root; 38 else{ 39 fail[u] = root; 40 Q.push(u); 41 } 42 } 43 while(!Q.empty()){ 44 int now = Q.front(); 45 Q.pop(); 46 for(int i = 0; i < 6; i++){ 47 int& u = nex[now][i]; 48 if(u == -1) 49 u = nex[ fail[now] ][i]; 50 else{ 51 fail[u] = nex[ fail[now] ][i]; 52 end[u] |= end[ fail[u] ]; 53 //last[u] = end[ fail[u] ]? fail[u] : last[ fail[u] ]; 54 Q.push(u); 55 } 56 } 57 } 58 } 59 }; 60 Tire ac; 61 62 double a[505][505], x[505], ans[505]; 63 int equ, var; 64 int Gauss(){ 65 int i,j,k,col,max_r; 66 for(k = 0, col = 0; k < equ&&col < var; k++, col++){ 67 max_r = k; 68 for(i = k+1; i < equ; i++) 69 if(fabs(a[i][col]) > fabs(a[max_r][col])) 70 max_r = i; 71 if(fabs(a[max_r][col]) < eps) return 0; 72 if(k != max_r){ 73 for(j = col; j < var; j++) 74 swap(a[k][j], a[max_r][j]); 75 swap(x[k], x[max_r]); 76 } 77 x[k] /= a[k][col]; 78 for(j = col+1; j < var; j++) a[k][j] /= a[k][col]; 79 a[k][col] = 1; 80 for(i = 0; i < equ; i++) 81 if(i != k){ 82 x[i] -= x[k]*a[i][k]; 83 for(j = col+1; j < var; j++) a[i][j] -= a[k][j]*a[i][col]; 84 a[i][col] = 0; 85 } 86 } 87 return 1; 88 } 89 90 int s[20]; 91 int main(){ 92 int n, l, t, ca = 1; scanf("%d", &t); 93 while(t--){ 94 ac.init(); 95 scanf("%d%d", &n, &l); 96 for(int i = 1; i <= n; i++){ 97 for(int j = 0; j < l; j++) 98 scanf("%d", s+j); 99 ac.insert(s, l, i); 100 } 101 ac.build(); 102 103 memset(a, 0, sizeof(a)); 104 memset(x, 0, sizeof(x)); 105 equ = ac.L, var = ac.L; 106 for(int i = 0; i < ac.L; i++) 107 a[i][i] = -1; 108 x[0] = -1; 109 for(int i = 0; i < ac.L; i++){ 110 if(!ac.end[i]) 111 for(int j = 0; j < 6; j++){ 112 int to = ac.nex[i][j]; 113 a[to][i] += 1.0/6; 114 } 115 } 116 117 Gauss(); 118 119 for(int i = 0; i < ac.L; i++) 120 if(ac.end[i]) ans[ ac.end[i] ] = x[i]; 121 for(int i = 1; i <= n; i++) 122 printf("%.6f%c", ans[i], " "[i == n]); 123 } 124 return 0; 125 }