1,深度优先(DFS):
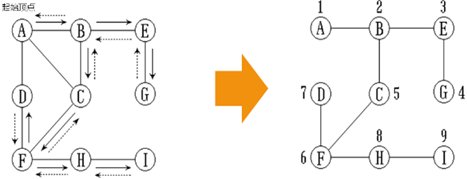
1,先选择一条边走,有多条边后,再选择一条走,直到无边可走,回退;
2,再选择另一条边走;
3,特点:只要在当前的顶点上面可以有边走到其它顶点,就深入的走下去;
2,深度优先算法:
1,原料:class LinkStack<T>;
2,步骤:
1,将起始顶点压入栈中;
2,弹出栈顶顶点 V,判断是否已经标记(标记:转 2,未标记:转 3);
3,标记顶点 V,并将顶点 V 的邻接顶点压入栈中;
4,判断栈是否为空(非空:转 2,空:结束);
3,深度优先算法示例:

4,深度优先算法流程图:
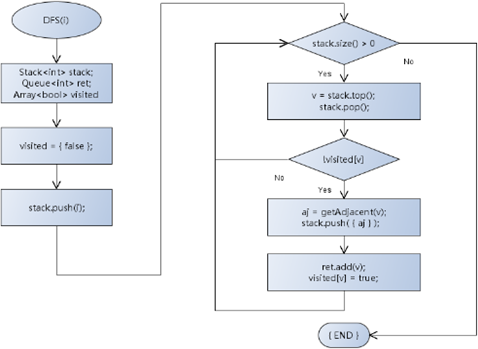
1,标记、压入邻接顶点;
5,深度优先算法实现:
1 /* 实现深度优先算法的函数;核心思想是二叉树先序遍历核心思想(非递归法版本) */ 2 SharedPointer< Array<int> > DFS(int i) 3 { 4 DynamicArray<int>* ret = NULL; // 返回值是一个数组 5 if( (0 <= i) && (i < vCount()) ) // 参数合法 6 { 7 LinkStack<int> s; // 压入邻接顶点的栈 8 LinkQueue<int> r; // 压入遍历值的队列 9 DynamicArray<bool> visited(vCount()); // 访问标记数组 10 11 /* 将标记里面的值初始化为未有访问 */ 12 for(int j=0; j<visited.length(); j++) 13 { 14 visited[j] = false; 15 } 16 17 s.push(i); // 初始顶点压入栈中 18 19 while( s.size() > 0 ) // 有顶点就要继续 20 { 21 int v = s.top(); // 得到栈顶的元素 22 23 s.pop(); // 弹出栈顶元素 24 25 if( !visited[v] ) // 顶点未有访问 26 { 27 SharedPointer< Array<int> > aj = getAdgacent(v); // 得到 v 的所有邻接顶点 28 29 /* 将 v 的所有邻接顶点压入栈中 */ 30 for(int j=aj->length()-1; j>=0; j--) 31 { 32 s.push((*aj)[j]); // 将邻接顶点逐个压入栈中 33 } 34 35 r.add(v); // 将 v 压入队列中 36 37 visited[v] = true; // 将 v 标记位已经访问 38 } 39 } 40 41 ret = toArray(r); // 将队列转换为数组 42 } 43 else 44 { 45 THROW_EXCEPTION(InvalidParameterException, "Index i is invalid ..."); 46 } 47 48 return ret; 49 }
6,深度优先算法实现的测试代码:
1 #include <iostream> 2 #include "MatrixGraph.h" 3 4 using namespace std; 5 using namespace DTLib; 6 7 int main() 8 { 9 MatrixGraph<9, char, int> g; 10 const char* VD = "ABEDCGFHI"; 11 12 for(int i=0; i<9; i++) 13 { 14 g.setVertex(i, VD[i]); //设置顶点相关的值为字符串 VD 中的内容 15 } 16 17 g.setEdge(0, 1, 0); // 无向图、特殊的有向图,所以每个点之间的邻接矩阵对称, 这里权值为 0,只关心是否连接,不关心权值 18 g.setEdge(1, 0, 0); 19 g.setEdge(0, 3, 0); 20 g.setEdge(3, 0, 0); 21 g.setEdge(0, 4, 0); 22 g.setEdge(4, 0, 0); 23 g.setEdge(1, 2, 0); 24 g.setEdge(2, 1, 0); 25 g.setEdge(1, 4, 0); 26 g.setEdge(4, 1, 0); 27 g.setEdge(2, 5, 0); 28 g.setEdge(5, 2, 0); 29 g.setEdge(3, 6, 0); 30 g.setEdge(6, 3, 0); 31 g.setEdge(4, 6, 0); 32 g.setEdge(6, 4, 0); 33 g.setEdge(6, 7, 0); 34 g.setEdge(7, 6, 0); 35 g.setEdge(7, 8, 0); 36 g.setEdge(8, 7, 0); 37 38 SharedPointer< Array<int> > sa = g.DFS(0); 39 40 for(int i=0; i<sa->length(); i++) 41 { 42 cout << (*sa)[i] << " "; 43 } 44 45 return 0; 46 }
7,如何使用二叉树先序遍历的思想遍历图?
1,深度优先思想使用的就是二叉树先序遍历的思想,先序遍历是递归完成的,深度优先算法也可以递归完成;
8,递归法实现深度优先:

1,问题划分;
2,定义功能:DFS(graph, vex)

1,以顶点 vex 为起始顶点深度优先遍历 graph;
3,功能函数代码实现:
1 /* 定义深度优先算法的递归函数 */ 2 template < typename V, typename E> 3 void DFS(Graph<V, E>& g, int v, Array<bool>& visited) 4 { 5 if( (0 <= v) && (v < g.vCount()) ) 6 { 7 cout << v << endl; // 访问的方式是打印 8 9 visited[v] = true; // 设置访问标记 10 11 SharedPointer< Array<int> > aj = g.getAdgacent(v); // 获取 v 的邻接顶点 12 13 /* v 是否有邻接顶点,有的话就递归进行深度优先算法的遍历 */ 14 for(int i=0; i<aj->length(); i++) 15 { 16 /* 如果没有进行访问,就进行深度优先遍历 */ 17 if( !visited[(*aj)[i]]) 18 { 19 DFS(g, (*aj)[i], visited); // 递归调用 20 } 21 } 22 } 23 else 24 { 25 THROW_EXCEPTION(InvalidParameterException, "Index v is invalid ..."); 26 } 27 }
4,深度优先代码实现:
1 /* 递归法深度优先遍历图,第一个参数是要被遍历的图,第二个参数是遍历的起始顶点 */ 2 template < typename V, typename E > 3 void DFS(Graph<V, E>& g, int v) 4 { 5 DynamicArray<bool> visited(g.vCount()); // 标记顶点是否被访问过 6 7 /* 为每一个顶点设置是否被访问的初始值 */ 8 for(int i=0; i<visited.length();i++) 9 { 10 visited[i] = false; 11 } 12 13 DFS(g, v, visited); 14 }
9,小结:
1,深度优先按照“先序遍历的方式”对顶点进行访问;
2,深度优先算法的核心是栈的使用;
3,深度优先和广度优先的唯一不同在于栈或队列的使用;
4,深度优先算法可以使用递归的方式实现;
1,深度优先使用栈来完成的并且是先序遍历的思想,则可以考虑使用递归的方式来实现;
2,当用栈来实现的时候,可以考虑使用递归;