2.1 描述定性数据的图形法和数值法
定义2.1
类(或组)频数:落入这个类中的观测值的个数
类(或组)相对频率:落入这个类中的观测值的个数相对于观测值总数的比例
定性数据描述常用条形图和饼图
条形图:给出每一类的频数(或频率),长方形的高度或长度与类频数(或频率)成比例
饼图:一个整圆分成几份,每一份代表一个类。没份中心角与类相对频率成比例。
帕累托图:讲定性变量(即长方形)的类(组)按照高度从左到右降序排列的条形图
2.2 描述定量数据的图形法
定量数据可以用三种图形法:点图,茎叶图,直方图
点图:数据集中每一个定量测量的数值表示为水平刻度尺上的而一个点,当数值重复时,点垂直画在另一个点之上
茎叶图:定量变量的数值分为茎叶两部分。茎按照顺序排在一列中,数据集中每一定量测量值的叶放在相应的茎的行上,
有相同茎的观察值的叶在水平方向按照升序排列
直方图:将观察值分成若干相同宽度的组区间,构成水平轴刻度,长方形高度等于组频数或相对频率。
构建茎叶图的步骤:1):把数据集中的每一观测值分为茎和叶两部分。例如:31.8的茎是31,叶是8
2) 将茎叶依次排成一列,从最小的茎开始到最大的茎结束
3)将每一个观察值的叶放在恰当的行上,一般同一行上的叶按升序排列
构建直方图的步骤:1):计算数据的极差
2): 将极差分成等间隔的组,数据少则分组少,多则分组多。选择适当的组宽,以便没有观察值落入边界。
经验法则:观测值个数少于25,组5-6个;观察值25-50,组7-14个,观察值大于50个,组15-20个。
3):对每一组,数出落入组中的观察值个数,该数值即为组频数
4):计算每一组的相对频率
5):直方图本质是条形图,其中类型就是组。频数(频率)直方图中,长方形的高由频数(频率)决定。
优劣:对与非常大的数据,直方图可以很好的直观描述,但无法给出单个测量值(即原始数据其实是经过了转化,所以无法展示原始数据)
相反,茎叶图及点图,每一个原始值都是可以很容易观察到,提供有用细节,但相对与大数据,会削弱直观效果,则显得不合适。
2.3 描述定量数据的数值法
数值描述性度量:数据集计算得到的数值,通常会通过三个类型的度量,帮助我们建立它的频率直方图的印象。
1)中心趋势度量:帮助确定频率分布中心位置的度量。算术平均(均值),中位数,众数。
2)变异的度量:围绕中心波动的度量。极差,方差,标准差
3)相对位置的度量:描述数据集中一个观察值相对位置的度量
定义2.3 统计量:由样本数据计算得到的数值描述性度量
定义2.4 参数:总体的数值描述性度量
1)中心趋势度量:
一般用μ表示总体均值,![]() 表示样本均值(或者横线下面是个y)
表示样本均值(或者横线下面是个y)
尽管均值是常用的中心趋势的度量,但是它对于非常大或非常小的观察值是非常敏感的,因此均值将移向偏度的方向( 分布的尾部),有时会产生误导。
中位数则不受极端值的影响,对于偏度极大的数据集,中位数能较好的描述数据分布的“中心”
很少用众数作为中心趋势的度量。
2)变异的度量:
定义2.8 极差:数据集中最大值与最小值的差值
定义2.9 样本方差:对于n个测量值的样本方差为:

对于n个测量值的有限总体,总体方差为:
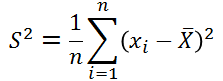
至于为什么样本方差要除以n-1而不是n的原因,查看微博https://blog.csdn.net/hearthougan/article/details/77859173。
两个数据集可能有相同的极差,但不同的变异性,因此极差是数据变异相对不敏感的度量。
方差有理论意义,但难于解释,因为对于感兴趣的变量x的度量单位是平方。
标准差的度量单位与x的单位相同,结合数据的均值。标准差容易解释。
解释标准差的两个有用的法则:经验法则和切比雪夫法则