KMP 算法是 D.E.Knuth、J,H,Morris 和 V.R.Pratt 三位神人共同提出的,称之为 Knuth-Morria-Pratt 算法,简称 KMP 算法。该算法相对于 Brute-Force(暴力)算法有比较大的改进,主要是消除了主串指针的回溯,从而使算法效率有了某种程度的提高。
例:输入一个字符串"aabaabaaf",模式串"aabaaf",求字符串是否包含该模式串。
常见字符串匹配算法:
使用暴力方法从字符串第一个字符开始匹配模式串,若不匹配从第二个字符开始从模式串的第一个位置开始重新扫描,时间复杂度为$O(n^2)$
class Solution {
public:
int strStr(string haystack, string needle) {
int nL = needle.length();
if (nL == 0)
return 0;
int hL = haystack.length();
int nIndex = 0, hIndex = 0;
while (hIndex < hL && nIndex < nL)
{
if (haystack[hIndex] == needle[nIndex])
{
hIndex++;
nIndex++;
}
else
{
hIndex -= nIndex - 1;
if (hL - hIndex < nL)
break;
nIndex = 0;
}
}
if(nIndex==nL)
return hIndex-nL;
return -1;
}
};
KMP算法描述:
在扫描字符串的时候只需一次扫描,需要构建next数组即next[i]表示当前最长公共前后缀的长度,匹配的时候若当前i无法匹配,则返回next[i-1]所在的数组下标。
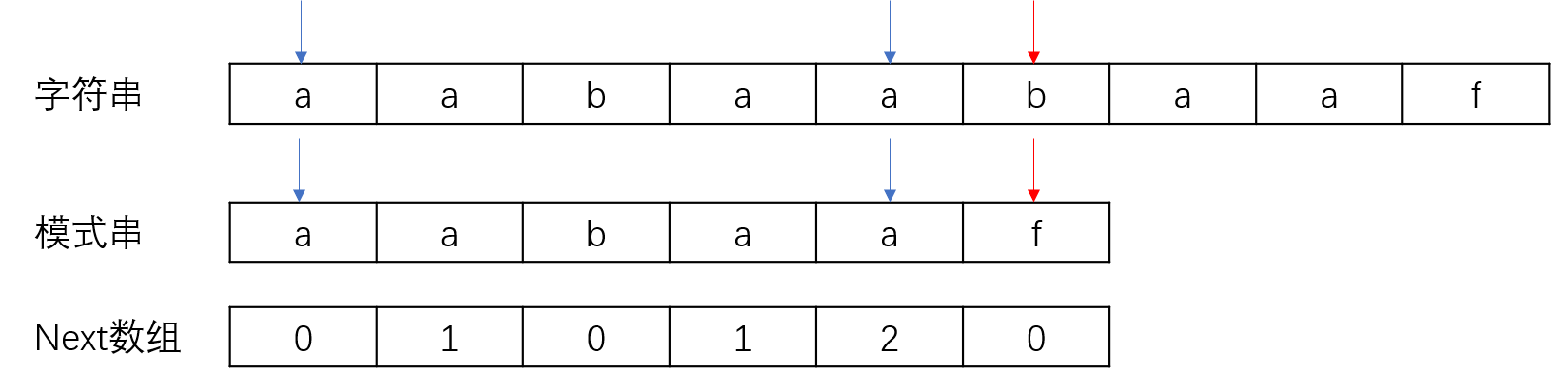
当在b和f不匹配的时候,返回到f的前一个位置的next[5-1]所对应的下标,即2的下标对应模式串中的b开始继续匹配,直到匹配完成
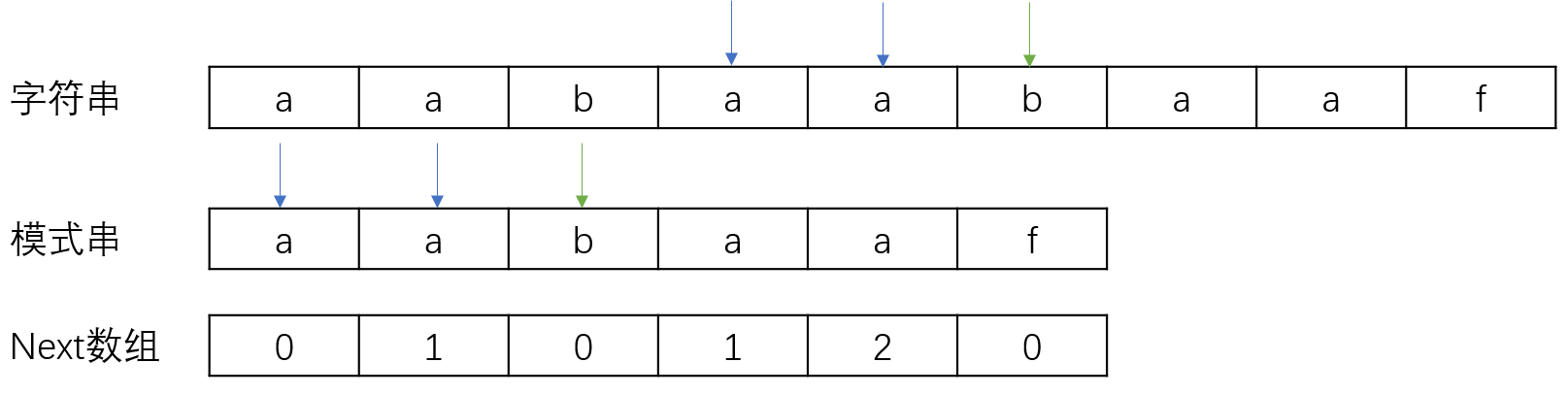
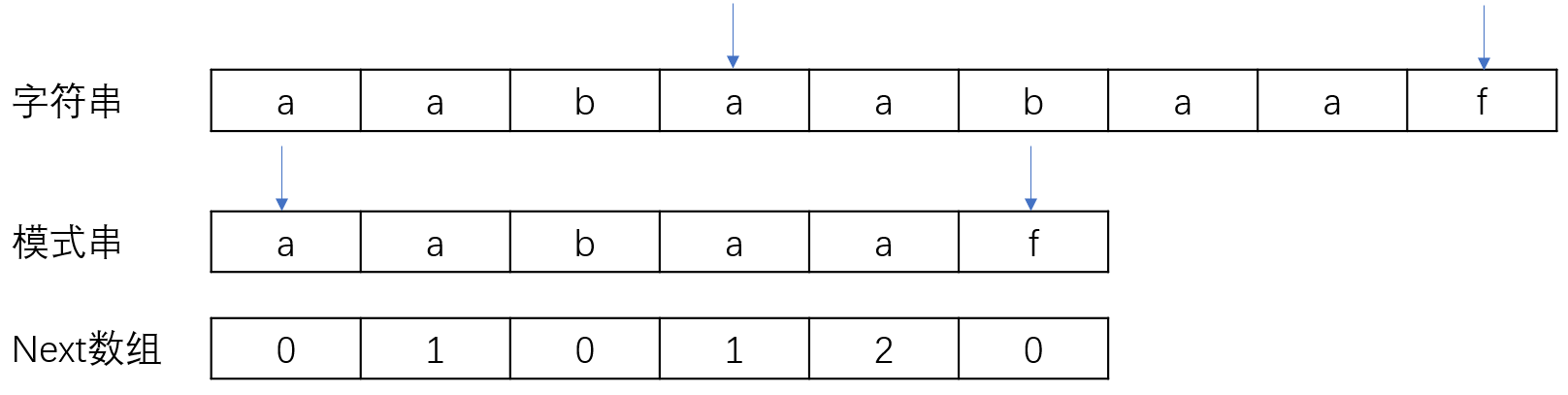
构建next数组
构建next数组,需要了解前后缀。模式串aabaaf的前缀有:a、aa、aab、aaba、aabaaf即不包含字符串本身,同理后缀有f、af、aaf、baaf、abaaf。
next数组有三种构建方法:
1)以0为初始下标,next数组构建后为:
| next | 0(a) | 1(aa) | 2(aab) | 3(aaba) | 4(aabaa) | 5(aabaaf) |
|---|---|---|---|---|---|---|
| val | 0 | 1 | 0 | 1 | 2 | 0 |
2) (1)式构建后去除最后一个元素向右移动,next[0]为-1,next数组构建后为:
| next | 0(a) | 1(aa) | 2(aab) | 3(aaba) | 4(aabaa) | 5(aabaaf) |
|---|---|---|---|---|---|---|
| val | -1 | 0 | 1 | 0 | 1 | 2 |
3)(1)式构建后所有元素-1,next数组构建后为:
| next | 0(a) | 1(aa) | 2(aab) | 3(aaba) | 4(aabaa) | 5(aabaaf) |
|---|---|---|---|---|---|---|
| val | -1 | 0 | -1 | 0 | 1 | -1 |
以上三式的构造next数组没有太大区别,只有后续计算的一些细节不同,本人习惯使用(1)式。
//KMP next数组计算
vector<int> getNext(string pat){
//初始化为0
vector<int> next(pat.size(), 0);
//j代表前一项最长公共前后缀的长度,也可看成前缀的下标
int j = 0;
//i代表后缀末尾的字符 因为1字符最长公共前后缀为0,故从第二个字符开始
for (int i = 1; i < pat.size(); i++)
{
//若i和j不同的话 利用next数组性质返回前一项的下标
while (j > 0 && pat[j] != pat[i])
{
j = next[j - 1];
}
//若相等此时长度+1
if (pat[j] == pat[i])
next[i] = ++j;
}
return next;
}
KMP算法代码,以LeetCode28为例:
class Solution
{
public:
//KMP next数组计算
vector<int> getNext(string pat)
{
//初始化为0
vector<int> next(pat.size(), 0);
//j代表前一项最长公共前后缀的长度,也可看成前缀的下标
int j = 0;
//i代表后缀末尾的字符 因为1字符最长公共前后缀为0,故从第二个字符开始
for (int i = 1; i < pat.size(); i++)
{
//若i和j不同的话 利用next数组性质返回前一项的下标
while (j > 0 && pat[j] != pat[i])
{
j = next[j - 1];
}
//若相等此时长度+1
if (pat[j] == pat[i])
next[i] = ++j;
}
return next;
}
int strStr(string haystack, string needle)
{
//KMP计算next数组
vector<int> next = getNext(needle);
int hIndex = 0, nIndex = 0;
while (hIndex < haystack.size() && nIndex < needle.size())
{
if (haystack[hIndex] == needle[nIndex])
{
nIndex++;
hIndex++;
}
else
{
if (nIndex != 0)
nIndex = next[nIndex - 1];
else
hIndex++;
}
}
if (nIndex == needle.size())
return hIndex - nIndex;
return -1;
}
};
KMP算法扩展Leetcode459:
题目链接 判断该字符串能否全部由字串构成。有一个公式: 字符串长度%(字符串长度-该字符串最长公共前后缀)==0,即True。
#include <bits/stdc++.h>
using namespace std;
class Solution
{
public:
bool repeatedSubstringPattern(string s)
{
int j = 0;
vector<int> next(s.size(), 0);
for (int i = 1; i < s.size(); i++)
{
while (j > 0 && s[j] != s[i])
{
j = next[j - 1];
}
if (s[j] == s[i])
next[i] = ++j;
}
//注意求0
return next.back() != 0 && s.size() % (s.size() - next.back()) == 0;
}
};