数学 必修三 第二章 统计

数学 必修三  第二章 统计  

一：随机抽样

　　从元素个数为N的总体中不放回地抽取容量为n的杨被，如果每一次抽取时总体中的各个个体有相同的可能性被抽到，这样抽样方法叫做简单随机抽样，这样抽取的样本，叫做简单随机样本。

　　6个同样质地的小球，从中不放回地抽取3个小球：

　　第一次抽取，6个中抽取1个 ，每个球的被抽取的可能性是1/6     并且是相等的

　　第二次抽取，5个中抽取1个，每个球被抽取的可能性都是1/5；

　　第三次抽取，4个中抽取1个，每个球被抽取的可能性都是1/4；

　　

　　常哟昂的简单随机抽样方法有抽签法和随机数表示法

　　1.抽签法

　　100个灯管寿命     不放回的抽取10个灯管的寿命构成简单的随机样本

　　方法：给100个灯管寿命编号，每一只灯管寿命对应1-100中的唯一一个数，再把这100个号码分别写道纸上，然后抽取 10个号码   ，和这10个号码对应的日光灯管寿命就构成了一个简单随机样本。

　　抽签法  比较简单    但是当总体的容量非常大时，并不适用，同时   总体要搅拌均匀。

　　2.随机数表法

　　随机数表   是由0，1，2，3，4...9这10个数字组成的鼠标，并且表中的每一位置出现各个数字的可能性相同。程序可生成随机数表，由5个数组成一组   ，然后通过随机数表来抽取样本。

　　案例：850颗种子的发芽率   从中抽取50颗种子进行实验   使用随机数表来抽取

　　步骤：

　　1.编号从001   002  ...850

　　2.给出的随机数是5位数一组 ，使用各个5位数组的前3位，从各组数中任选一个前3为小于或等于850的数作为起始号码。例如从第一行第7组数字开始，取530作为抽取的50颗种子中的第1个的代号。接着继续向右读取   如果遇到大于850的数字  则跳过，取到50个数字即可。

　　　　　　　　　　　　随机数表例子   

 

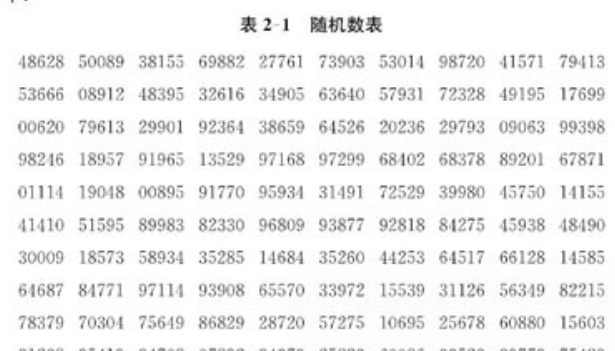
　　数字随机数生成： c++          dev c++编译器        linux系统    以下程序可以生成上面的图片

#include <iostream>

#include <cstdlib>
#include <ctime>

#define random(a,b) (rand()%(b-a)+a) 　　　//宏定义 用于扩展

using namespace std;

int main()
{
　　srand((unsigned ) time(NULL));　　　　  //随机数种子
　　for(int i=0;i<85;i++)　　　　　　　　　　//共850个数字
　　{
　　　　for(int j=0;j<10;j++)
　　　　　　{
　　　　　　　　cout<<random(10000,99999)<<" "; 　　//random   产生  10000到99999之间的随机数
　　　　　　}
　　　　cout<<" ";　　　　　　　　　　　   //10个数一行  之后换行   
　　}
　　return 0;
}

　　c++没有自带的random函数，要实现随机数的生成就需要使用rand和srand 

　　1.rand()   仅仅返回一个0至RAND_MAX之间的随机数 ，而RAND_MAX的值与int位数有关，最小是32767.不过rand()是一次性的，因为系统默认的随机数种子为1，只要随机数种子不变，其生成的水技术序列就不会改变。

　　2.srand()   可以用来设置rand()产生随机数时的随机数种子。通过设置不同的种子以获得不同的随机数序列。

　　产生不同随机数种子的方法：srand( unsigned int ) ( time(NULL))   利用系统的时钟  来产生不同的随机数种子

　   调用time()  需要加入头文件  <ctime>

#include<iostream>

#include<cstdlib>
#include<ctime>
　using namespace std;
int main()
{
　　srand((unsigned)time(NULL));　　//生成种子
　　for(int i=0;i<10;i++)
　　　　cout<<rand()<<' ';   　　　　  //产生随机数
　　return 0;
}

通式

产生一定范围随机数的通用表示公式是：

• 取得(0,x)的随机整数：rand()%x；
• 取得(a,b)的随机整数：rand()%(b-a)；
• 取得[a,b)的随机整数：rand()%(b-a)+a；
• 取得[a,b]的随机整数：rand()%(b-a+1)+a；
• 取得(a,b]的随机整数：rand()%(b-a)+a+1；
• 取得0-1之间的浮点数：rand()/double(RAND_MAX)。

 练习A

　　全班同学爱听数学课的比例  计划抽取8名同学做调查，请你用抽签法抽取一个样本。

　　假设共50名学生   从1-50编号 贴纸条或小球，然后每次从总体中抽取一个，直到取第8个时停止，在抽取的过程中，每个小球被抽取的可能性都是1/当时的总数，之后再查看这8名学生爱听数学课成为样本。

练习B1

　　某居民区有730户居民，居民会计划从中抽取25户调查其家庭收入状况，利用简单随机样本来统计。

　　730户居民编号000-730；

　　随机生成730个数字，每个数字由5个个位数组合而成。取后3位数为整数，大于730的数需要跳过，共取25个。

练习B2

　　制作1000个一位数的随机数表，并检查0-9这10个数在表中出现的可能性是否相同？

　　代码：

// 生成1000个0-3的数字组成的随机数表 

#include <iostream>
#include <cstdlib>
#include <ctime>

#define random(a,b) (rand()%(b-a+1)+a) //宏定义

　　using namespace std;

int main()
{
　　srand((unsigned ) time(NULL));
　　　int cn0=0;
　　　int cn1=0;
　　　int cn2=0;
　　   int cn3=0;
　　   int number=0;
　　for(int i=0;i<100;i++)
　　{
　　　　for(int j=0;j<10;j++)
　　　　{
　　　　　　number=random(0,3);
　　　　　　if(number==0)
　　　　　　{
　　　　　　　　cn0++; //0的数字个数
　　　　　　}
　　　　　　else if(number==1)
　　　　　　{
　　　　　　　　cn1++; //1的数字个数
　　　　　　}
　　　　　　else if(number==2)
　　　　　　{
　　　　　　　　cn2++; //2的数字个数
　　　　　　}
　　　　　　else if(number==3)
　　　　　　{
　　　　　　　　cn3++; //3的数字个数
　　　　　　}
　　　　　　　　cout<<number<<" ";
　　　　}　　
　　　　　　cout<<" ";
　　}
　　　　cout<<"0的个数为："<<cn0<<";;;1的个数为："<<cn1<<";;2的个数为："<<cn2<<";;3的个数为："<<cn3<<endl;
　　　　cout<<"总数为："<<cn0+cn1+cn2+cn3<<endl;
　　　　return 0;
}

　    0-3  之间选择随机数    事实是相同的   

二.系统抽样　　

　　当总体数量非常大的时候，样本容量就不宜太小，采用简单随机抽样，就显得费事，可将总体分成均衡的若干部分，然后按照预先指定的规则，从每一部分抽取一个个体，得到所需要的样本，这种抽样的方法叫做系统抽样。

　　案例1：高一学生期末考试数学成绩统计，从参加考试的15000名学生的数学成绩中抽取容量为150的样本。对全体学生的数学成绩进行编号。号码从1-15000。

样本容量为150，总体容量为15000  这样两个的比例为150：15000=1：100。     

　　将总体平均分成150个部分，其中每个部分包含100个号码；在1-100中抽取一个号码假设为56，则第二个数为156，以后的一次递增100 即256、356...

　　直到取得150个号码为止：序列为：56，156，256，356，456，....

　　得到150个号码学生的成绩为样本

　　

　　从元素个数为N的总体中抽取容量为n的样本，如果总体容量能被样本容量整除，设定k=N/n，先从数字1到k中随机地抽取一个数s作为起始数，然后顺次抽取第s+k，s+2k，...，s+(n-1)k个数，这样就得到容量为n的样本。如果总体容量不能被样本容量整除。可随机地从总体中剔除余数，然后再按照系统抽样方法进行抽样。

　　进行大规模的抽样调查时，系统抽样比简单随机抽样要方便得多，因而应用的范围很广。由于抽样的间隔相等，因此系统抽样也被称为等距抽样。

练习A：1563个产品中   抽取15件产品做检测    给出系统抽样方案

　　1.1-1563编号        1563/15=104.2   四舍五入  取104

　　2.1-104中取1个数字  假设为87    之后取87+1*104=191        再之后是87+2*104=295     再之后是87+3*104   等等  一直取15个数

　　3.此15个数字组成样本空间

练习B：

　　总数为365天  

　　编号从1-365

　　365/52=7.01        约等于7

　　所以1-7中任选一个数字  假设为5   则第2个数为5+7=12     第3个数为5+14=19     第4个数为5+3*7=26    一直取满52个数。

　　这52个数字组成样本空间。

　　案例代码：

　　

//系统抽样     生成52个随机数

#include <iostream>
#include <cstdlib>
#include <ctime>

#define random(a,b) (rand()%(b-a+1)+a)

using namespace std;

int main()
{
srand((unsigned)time(NULL)); //生成种子
int number=365;
int parts=52;
int n=number/parts;
int c=0;
int a=random(1,7);

for(int i=0;i<52;i++)
{
cout<<a+c*n<<endl;
c++;
}
// cout<<n<<" ";

return 0;
}

分层抽样

　　当总体由明显差别的几部分组成时，为了使抽取的样本更好地反映总体的情况，常常采取分层抽样，将总体中各个个体按某种特征分成若干个互不重叠的几部分，每一部分叫做层，在各层中按层在总体中所占比例进行简单随机抽样或系统抽样，这种抽样方法叫做分层抽样。

　　案例：某高中900名学生  考察体重，抽取45名学生的体重组成的样本，因为各个年级的学生随着年龄的增长体重不同，所以分三层来抽取

　　高一学生共400名;高二学生300名;高三学生200名; 

　　样本容量与总体容量的比为45：900=1：20

　　所以45=900*1/20=（400+300+200）*1/20=400*1/20+300*1/20+200*1/20=20+15+10=45

　　所以高一，高二，高三3个层面上取的学生数分别为：20     15     10

　　然后再分别对各层进行简单随机抽样；分层的优点是  具有较强的代表性   而且在各层抽样时可以灵活地选用不同的抽样法

练习1：

　　500名学生  喜欢数学的学生占30%，不喜欢数学的占40%，介于两者之间的学生占30%，为了考查学生的其中考试的数学成绩，如何用分层抽样来抽取一个容量为50个样本。

　　成绩高的（喜欢数学）  500*30%=150

　　成绩中等的　　　　　  500*30%=150

　　成绩低的　　　　　　  500*40%=200

　　样本为50：总体500=1：10

　　所以分层抽取的数量为：150/10=15；150/10=15；200/10=20    

　　分别为成绩高的      成绩中等的     成绩低的     总数为50

　　然后再分别对各层进行简单随机抽样  　

练习2：某公司500人，其中不到35的125人，35-49的280人      50岁以上的95人   为了调查员工的身体健康状况 样本为100名 分层抽取的方法

　　100/500=1/5

　　35岁的抽取  　　　　125/5=25人　　再简单随机抽取

　　35-49岁的抽取　　　280/5=56人　　

　　50岁以上　　　　　  95/5=19人　　

练习3：饮食习惯   1500为总数，抽取200名进行调查

　　南方人500名      北方人800名    西部地区200名

　　方法：

　　200/1500=2/15

　　南方人抽样为500*2/15=66.6=67人

　　北方人抽样为800*2/15=106人

　　西部地区的人抽样为200*2/15=26.6=27人

　　合计共200人

练习B：

　　12000 分别来自四个城区   其中东城区2400人，西城区4605人，南城区3795人，北城区1200人

　　从中抽取60人

　　方法如下：

　　1.计算比例

　　　　60/12000=1/200

　　2.分别计算

　　　　2400/200=12

　　　　4605/200=23

　　　　3795/200=19

　　　　1200/200=6

　　合计12+23+19+6=60

　　3.然后分别对四个城区进行简单的随机抽样 统计

上题中的程序代码：

1.simplesample.h    头文件

class randsample
{
public:
randsample();
randsample(int _s,int _n);
void sample();
void print();
private:
int num;//样本容量
int sum;//总量
int samples[];
};

 2.simplesample_class_implement.cpp

//simplesample类的实现

//implement simple_sample

#include <iostream>
#include <ctime>
#include <cstdlib>
#include "simplesample.h" //用户自定义的文件

#define random(a,b) (rand()%(b-a+1)+a) //宏定义

using namespace std;

randsample::randsample()
{

cout<<"default"<<" ";
sum=0;
num=0;
samples[0]={0};
}

randsample::randsample(int _s,int _n)//形参为总量和样本数量
{
sum=_s;
num=_n;

}
void randsample::print()
{
int count=0;
cout<<"样品容量为："<<num<<" ";
cout<<"总量为："<<sum<<" ";
sample();
cout<<"抽取的样品编号分别为： ";
for(int i=0;i<num;i++)
{
count++;
cout<<"第"<<i+1<<"个:"<<samples[i]<<" ";
if(count%5==0)
cout<<" ";
}
}
void randsample::sample()
{
for(int i=0;i<num;i++)
samples[i]=random(0,sum);
}
int main()
{
srand((unsigned)time(NULL));//产生随机数种子，如果不设置 则rand()值始终为1 则每次生成的随机数都是相同的
randsample dongcheng(2400,12);
dongcheng.print();
cout<<" ";
cout<<" ";
randsample xicheng(4605,23);
xicheng.print();
cout<<" ";
cout<<" ";
randsample nancheng(3795,19);
nancheng.print();
cout<<" ";
cout<<" ";
randsample beicheng(1200,6);
beicheng.print();
cout<<" ";
cout<<" ";
return 0;
}

2.1.4  数据的收藏

 　　在实际统计时  要确定调查的目的、对象   即统计调查要解决的问题和需要调查的总体；

　　要确定好调查的项目，也就是要统计的变量，接下来就可以开始收集数据了

　　1.试验

　　能够直接获得样本数据     例如投骰子  

　　2.查阅资料　　

　　查阅理念文献  统计年鉴等    例如  全国历次人口普查的数据

　　3.设计调查问卷

　　由一组有目的，有系统，有顺序的题目组成。

　　问题要具体，有针对性   

　　避免一般性或者不具体的问题

　　语言简单、准确、含义清楚  避免出现有歧义或意思含混的句子

　　不能出现引导受调查者答题倾向的语句

　

汇总练习题

　　习题2-1_A

　　1.某地10000名高一学生的体重   抽取200名雪深更调查

　　　　总体：10000名学生的体重情况

　　　　个体：每名学生的体重

　　　　样本：是10000名中抽取的200名学生的体重情况

　　　　总体容量：10000

　　　　样本容量：200

　　2.编号为1-100的100道题中随机抽取20道题组成考卷

　　　　总体：100

　　　　编号1-100

　　　　样本为20

　　　　不放回地每次抽取1个标签  纸条   组成样本　直到抽出20个纸条

　　3.590件货物   从中选出50件货物    用随机数表示法给出抽样方案

　　　　数字00100-99999   为范围

　　　　#define  random(a,b)  (rand()%(b-a+1)+a)

　　　　random(100,99999)

　　　　取得出的随机数   取每组数字的高三位  大于590的跳过

　　　　int num[50]={0};

　　　　int count=0;

　　　　for(int i=0;i<50;i++)

　　　　{

　　　　　　num[i]=random(0,999);

　　　　　　cout<<num[i];

　　　　　　count++;

　　　　　　if(count%7==0)

　　　　　　cout<<" ";

　　　　}

　　4.　10000人     编号0-9999   从这些游客当中随机选出10名幸运游客   用系统抽样的方式给出游客的编号    等距离抽取

　　　　　k=10000/10=1000;

　　　　　int n=random(0,1000);

　　　　　int m[10]={0};

　　　　　m[0]=n;

　　　　  cout<<"第1次抽取的样本为："<<m[0]<<" ";

　　　　　for(int i=1;i<10;i++)

　　　　　{

　　　　　　m[i]=n+i*k;

　　　　　　cout<<"第"<<i+1<<"次抽取的样本为："<<m[i]<<" ";

　　　　　}

      

代码示例：

//习题4 统计与抽样
#include <iostream>
#include <ctime>
#include <cstdlib>
#define random(a,b) (rand()%(b-a+1)+a)
using namespace std;
int main()
{
srand((unsigned)time(NULL));
cout<<"请输入总体容量:"<<endl;
int n1;
cin>>n1;
cout<<"请输入样本容量:"<<endl;
int n2;
cin>>n2;
int k=n1/n2;
int n=random(0,k);//calculate
int m[n2]={0};//initial set
m[0]=n;
cout<<"the first sample："<<m[0]<<" ";
for(int i=1;i<n2;i++)
{
m[i]=n+i*k;
cout<<i+1<<"th sample："<<m[i]<<" ";//输出所有的样品值
}
return 0;
}

5.

//simplesample 声明
/* 仅声明
*/

class randsample
{
public:
randsample();
randsample(int _s,int _n);
void sample();
void print();
private:
int num;//样本容量
int sum;//总量
int samples[];
};

class dividefun
{
public:
dividefun();//constructor default
dividefun(int _num,int _sum_samplenum); //初始化分层总体数组
void calculate();//计算分层样本的容量 并存入对应数组中
private:
int sample_num[]; //用来存储各个分层的样本容量的数组
int sum_num[]; //用来存储各个分层的总体容量的数组
int dividenum;//层数
int sum_samplenum;
};

//simplesample类的实现    未完成

//implement simple_sample

#include <iostream>
#include <ctime>
#include <cstdlib>
#include "simplesample.h" //用户自定义的文件

#define random(a,b) (rand()%(b-a+1)+a) //宏定义

using namespace std;

randsample::randsample()
{
cout<<"default"<<" ";
sum=0;
num=0;
samples[0]={0};
}
randsample::randsample(int _s,int _n)//形参为总量和样本数量
{
sum=_s;
num=_n;
}
void randsample::print()
{
int count=0;
cout<<"样品容量为："<<num<<" ";
cout<<"总量为："<<sum<<" ";
sample();
cout<<"抽取的样品编号分别为： ";
for(int i=0;i<num;i++)
{
count++;
cout<<"第"<<i+1<<"个:"<<samples[i]<<" ";
if(count%5==0)
cout<<" ";
}
}
void randsample::sample()
{
for(int i=0;i<num;i++)
samples[i]=random(0,sum);
}

//class dividefun implement

dividefun::dividefun(){
cout<<"default"<<endl;
sum_num[0]={0};
sample_num[0]={0};
dividenum=0;
}
dividefun::dividefun(int _num,int _sum_samplenum){
//int num=0;
sum_samplenum=_sum_samplenum;
dividenum=_num;
cout<<"请输入"<<dividenum<<"个数字:"<<endl;
for(int i=0;i<_num;i++)
{
cin>>sum_num[i];//初始化分层总量数组
}
}

void dividefun::calculate()//计算
{
int sum;
int k;
if(dividenum==0)
exit(1);
else
{
//计算总体抽样的比例
for(int i=0;i<dividenum;i++)
sum+=sum_num[i];
k=sum_samplenum/sum; //计算比例
for(int i=0;i<dividenum;i++)
{
sample_num[i]=sum_num[i]*k;//初始化分层样本数组
}
}
}

int main()
{
srand((unsigned)time(NULL));//产生随机数种子，如果不设置 则rand()值始终为1 则每次生成的随机数都是相同的
randsample dongcheng(2400,12);
dongcheng.print();
cout<<" ";
cout<<" ";
randsample xicheng(4605,23);
xicheng.print();
cout<<" ";
cout<<" ";
randsample nancheng(3795,19);
nancheng.print();
cout<<" ";
cout<<" ";
randsample beicheng(1200,6);
beicheng.print();
cout<<" ";
cout<<" ";
return 0;
}

2.2用样本估计总体

　　随机抽样的方法在总体中抽取样本   得到一组数据    可以用样本的频率分布估计总体的分布，可以用样本的数字特征（如平均数、标准差）估计总体的数字特征。

2.2.1用样本的频率分布估计总体的分布

　　将大量的数据样本，形成频数分布或者频率分布  可以比较清楚地看出样本数据的特征，从而估计总体的分布的情况。

　　制作频率分布表、频率分布直方图

　　1.计算极差

　　 极差是最大值与最小值的差   反映了一组数据变化的幅度  又叫全距

 　   将样本数据存入数组   ，设定temp临时值

　　 求出数组中的最大值==》max

 　　求出数组中的最小值==》min

　　 极差=max-min

　　2.决定组数与组距

　　样本数据有100个，可以分成8-12组   这里取11组   假设极差为0.32

　　所以  组距=极差/组数=0.32/11=0.03

　　3.决定分点

　　将第一组的起点定位25.235     组距为0.03    这样所分的11组分别是

　　1.       25.235～（25.235+0.03=25.265）

 　   2.　　25.265～25.295

　　...

　　11.　　25.535-25.565

　　极差=最大-最小=25.565-25.235=0.33（约）

 　　4.列频率分布表

　　 对落在各个小组内数据的个数进行累计，这个累计数叫做各个小组的频数，各个小组的频数除以样本容量，得各小组的频率。

　　求各小组频数的算法

　　第一步：设B（j） 为落在第j个小组内的数据个数，且B(j)=0(j=1,2,...,11);     B为分组的数组

　　第二步：逐一判断A(i)(i=1,2,...,100)落入哪一个小组，若落入第j个小组，则B(j)=B(j)+1　　A数组为样本数据

　　频率分布图如下：

　　

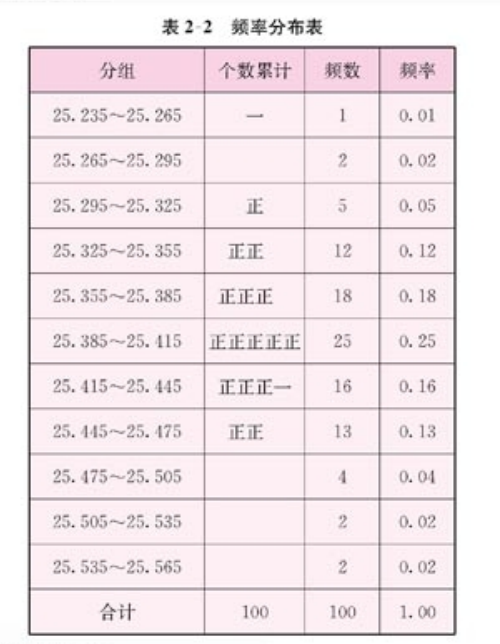
　　第三步  绘制频率分布直方图

　　　　在直角坐标系中，用横轴表示产品内径尺寸，纵轴表示频率与组距的比值，得到频率分布直方图。

　　　　

 　　　　在图中可以看出：

　　　　　　小长方形面积=组距*频率/组距=频率

　　　　　　各个小长方形的面积等于相应各组的频率，所有长方形面积之和等于1

　　　　优等品所占比例，可以统计出内径尺寸在区间25.325～25.475内的个体数在样本容量中所占的比例，也就是它的频率。

　　　　0.12+0.18+0.25+0.16+0.13=0.84

　　　　可以估算优等品比例为84%

　　　　频率分布折线图   将上图中的各个长方形的上边的重点用线段连接起来  就得到频率分布折线图

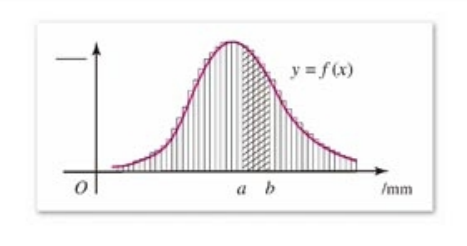
 　　　　样本容量不断增大，分组的组距不断缩小，则频率分布直方图实际上越来越接近于总体的分布，它可以用一条y=f(x)来描绘

　　　　这条光滑的曲线就叫做总体密度曲线。

 　　　　总体密度曲线精确地反映了一个总体在各个区域内取值的规律，产品尺寸落在（a,b）内的百分率就是图中带斜线部分的面积。

　　　　

 　　　　常用的统计图表  还有茎叶图

 　　　　案例：某赛季甲，乙两名篮球运动员每场比赛的得分情况如下：

　　　　甲得分：12，15，24，25，......

　　　　乙得分：8，13，14，16，23...

　　　　

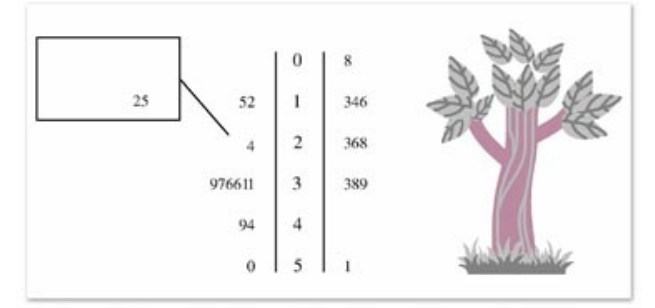
 　　　　中间的主干（茎）表示得分的十位上的数字     外面的表示各位上的数字

　　　　例如346就代表 13      14    16   三个得分

　　　　左边的为甲的得分               右边的为乙的得分

　　　　优点是没有原始信息的丢失

　　　　

练习A

　　1.一批灯泡中抽取50只寿命测试

　　　　

 2.2.2  用样本的数字特征估计总体的数字特征

　　通常往往不需要了解总体的分布形态，而是更加关心总体的某一数字特征。

 　  例如灯泡的寿命，了解一批灯泡的平均使用寿命。

　　把这批灯泡寿命看做总体，从中随机取出若干个个体作为样本，算出样本的数字特征，用样本的数字特征（如平均数）来估计总体的数字特征

　　1.用样本的平均数估计总体平均数

　　2.用样本标准差估计总体标准差

　　　　数据的离散程度可以用极差、方差或标准差来描述。

　　　　样本方差描述了一组数据围绕平均数波动的大小     样本方差的算术平方根。

　　　　

 　　　　极差为最大值减最小值

　　　　 方差的平方根为样本的标准差

 　　　　例5  甲乙 射击比赛

　　　　

#include <iostream>
#include <math.h>

using namespace std;

float bzc(int * group,int n,float &average);

int main()
{
    int A[]={7,8,6,8,6,5,9,10,7,4};
    int B[]={9,5,7,8,7,6,8,6,7,7};
    int sum=0;
    float Baverage,Aaverage;
    float Abzc,Bbzc;
    Abzc=bzc(A,10,Aaverage);
    Bbzc=bzc(B,10,Baverage);
    cout<<Aaverage<<":::::"<<Baverage<<endl;
    cout<<Bbzc<<"::::::"<<Abzc<<endl;
    return 0;
}
float bzc(int * group,int n,float &average)
{
    int C[n];
    int sum=0;
    for(int i=0;i<n;i++)
    {
        sum+=group[i];
    }
    average=sum/n;
    for(int i=0;i<n;i++)
    {
        C[i]=group[i]-average;
        C[i]*=C[i];
    }
    sum=0;
    for(int i=0;i<n;i++)
    {
        sum+=C[i];
    }
    float bzc=sqrt(sum/n);
    return bzc;
}

2.3变量的相关性

　　2.3.1  变量间的相关关系

　　一类是确定性的函数关系       例如边长与面积   正方形

　　另一类是有关系，但是并不是类似函数在的那种确定性       而是随机的   例如人的身高和体重

　　

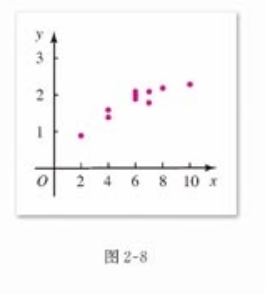
　　散点图  ：y随x的增大而增大    这种相关性叫做正相关      反之  叫做负相关

2.3.2  两个变量的线性相关

　　6天 热茶杯数与当天天气温度的对比图表

　　

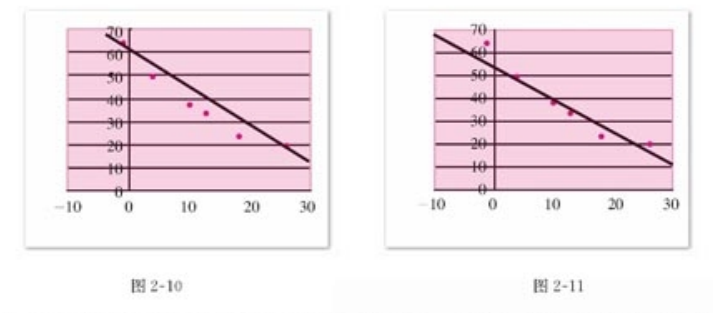
 　　近似的直线，图a为连接两个端点      图b为让这些点位于直线的上下的数目相等，

　　 根据不同的标准分配的      找出最佳的近似直线  （最优拟合直线）

　　 假设2-11 最标准，记   y'=a+bx ..........1       此时y'是为了区分Y实际的y值，

　　当x(i=1,2,3...6)时，Y的相应观察值为yi，    而直线上对应的xi的纵坐标是y'i=a+bxi       

　　　　1式叫做Y对x的回归直线方程，b叫做回归系数。

　　        确定方程    只要确定a与回归系数b即可。

　　如何证明最小二乘法中  a和b的公式    ？？？？？

　　　

 

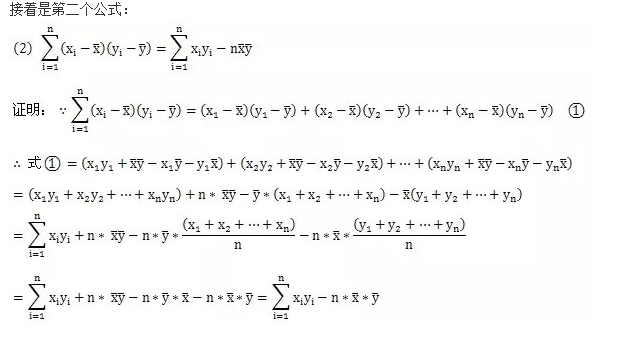
习题：

　　1.采用简单随机抽样从含10个个体的总体中抽取一个容量为4的样本，个体a前两次未被抽到，第三次被抽到的概率为______

 　　　答：第一次没有抽到的概率是9/10，第一次没有抽到且第二次也没有抽到的概率是9/10*8/9

　　　　第一次  第二次没抽到且第三次抽到的概率是9/10   *8/9   *1/10=1/10

 　　特点：

　　　　1.简单随机抽样从含有N个个体的总体中抽取一个容量为n的样本时，每次抽取一个个体时任一个个体被抽到的概率为1/N（N是变化的）；

　　　　　在整个抽样过程中各个个体被抽到的概率为n/N；

　　　　2.逐个抽取，且各个个体被抽到的概率相等。

　　　　3.不放回抽样；逐个地进行抽取；它是一种等概率抽样