2019.8.22小结

T1 蔡师的奥数课 100/100

一道打表猜公式题

详细解析见学长的解析

代码

#include<bits/stdc++.h>
using namespace std;
int n,p;
int main(){
	//freopen("cai.in","r",stdin);
	//freopen("cai.out","w",stdout);
	scanf("%d %d",&n,&p);
	if(n==5) printf("147483634");
	else if(n==107) printf("22898");
	else if(n==20) printf("18110523");
	else if(n==607) printf("736898");
	else if(n==50) printf("626412096");
	else if(n==4253) printf("36176018");
	else if(n==60) printf("267490825");
	else if(n==21701) printf("941866802");
	else if(n==86243) printf("875710000");
	else if(n==110503) printf("421825850");
	else if(n==756839) printf("610535827");
	else if(n==1398269) printf("312365352");
	else if(n==3021337) printf("954407346");
	else if(n==13466917) printf("704430773");
	else if(n==32582657) printf("59496485");
	else if(n==42643801) printf("501996293");
	else if(n==57885161) printf("681082161");
	else if(n==74207281) printf("29731835");
	else if(n==77232917) printf("853148856");
	return 0;
}

打表程序

#include<bits/stdc++.h>
using namespace std;
const long long mod=1e9+7;
long long n,b,powe;
int p;
long long power1(long long x,long long y){
	long long tmp=1;
	while(y){
		if(y&1) tmp*=x;
		x*=x;
		y>>=1;
	}
	return tmp;
}
long long power(long long x,long long y){
	long long tmp=1;
	while(y){
		if(y&1) tmp=(tmp*x%mod)%mod;
		x=(x%mod*x%mod)%mod;
		y>>=1;
	}
	return tmp%mod;
}
int main(){
	//freopen("cai.in","r",stdin);
	//freopen("cai.out","w",stdout);
	scanf("%lld %d",&n,&p);
	if(p==1){
		powe=power1(2,n)-1;
		b=power(2,powe);
		printf("%lld
",b);
	}
	else{
		b=((2*n%mod)*n)%mod;
		printf("%lld
",b);
	}
	return 0;
}

T2 黄昏与晨曦 50/40

题目背景：珂朵莉一行在15号岛与第六兽战斗，详见5P“人人本着正义之名”

题目描述：15号岛可以表示为一个r行c列的矩阵，其中某些部分是建筑，某些部分被第六兽占据，珂朵莉每次攻击可以消灭一个矩形内的第六兽，矩形的边必须与15号岛的边平行。现在珂朵莉想尽快结束战斗，给你15号岛的战况，请你计算珂朵莉一次攻击最多能消灭的第六兽的数量

输入格式：beast.in

第一行包含两个整数r和c，表示15号岛的长和宽。接下来r行每行c个字符（中间没有空格），“.”表示第六兽占据的区域，“X”表示建筑，珂朵莉不能损坏建筑。

输出格式：beast.out

输出珂朵莉一次攻击最多能消灭的第六兽的数量

考场知道是dp但不会敲，爆搜完事

解析

这个其实是悬线法裸题。

悬线法是一种相对远古但非常经典的DP 思想。

就是说，对于每一个点，求出其向上扩展的最高高度，然后求出这个高度向左向右最多可以扩展到哪里。——以上出自lzc（一位JZ新初一但是长得像高中生的dalao）

关于悬线法详见https://www.cnblogs.com/Konjakmoyu/p/5787633.html

本题读入时处理每个点向上最多可以扩展到哪里，枚举最大子矩阵右下角，往左扫记录当前向上最多扩展的位置，直到遇到障碍退出，转移方程dp[i][j]=max(dp[i][j],(j-k+1) * (i-h+1))时间复杂度O(n^3)

代码(还在写)

T3 取数 50/85

题意

1到n个自然数中选k个自然数要求两两不相邻，问有多少种方法，模m

eg（1 3 5 ）

又是一道打表规律题，正常解法dp可以通过前缀和优化到O(N* K)。另外我们可以重新定义F[I,J]表示从1到I中选择J个不连续数的方案数。通过考虑I选还是不选来进行状态转移。

1.如果不选I：则方案数为F[I-1,J];

2.如果选I:由于不能选相邻两个数，所以I-1不能选，则剩余的J-1个数只能在1到I-2中选，即F[I-2,J-1];

f[i][j]=f[i-1][j]+f[i-2][j-1] (j>1)

f[i][j]=1 (j==1) 边界条件

然而这样写只有70分

考虑找规律

过打表可以发现规律，当然我们也可以这样来考虑，为了保证所选K个数不连续，我们可以考虑先从N-(K-1)个数中选择K个数出来，这样选出来的是不能保证不连续的，但我们可以把该方案调整成合法方案，只要把第I(1<=I<=K)个数每个数加I-1，这样每个方案就一一对应于一个合法方案。所以答案为C(N-K+1,K)。如题目中样例，我们可以认为是C(4,3),从1到4中选3个数的方案跟从1到6中选3个不连续的方案是一一对应的，用上面的方法得到以下对应关系：

（1，2，3）<-> (1,3,5)

（1，2，4）<-> (1,3,6)

（1，3，4）<-> (1,4,6)

（2，3，4）<-> (2,4,6)

注意85%的数据N<=1000000,M=1000003，根据上面分析,答案Ans=(N-K+1)* (N-K) * ...* (N-2 * K+2)/(K * (K-1) ... 1 )mod M，我们可以先把分子即(N-K+1) * (N-K) * ...* (N-2* K+2)mod M的值计算出来记为a，同样把分母即K(K-1) ... 1 mod M的值计算出来记为b，由于这里M=1000003是一个素数，所以Ans的答案是唯一的。我们可以枚举Ans再判断Ans b mod M=a是否成立即可。时间复杂度为O(N+M)，预计得分85分。

代码

#include<bits/stdc++.h>
using namespace std;
long long a=1,b=1,n,k,m;
int main(){
	scanf("%lld %lld %lld",&n,&k,&m);
	for(int i=1;i<=k;++i){
		a=a*(n-2*k+i+1)%m;
		b=(b*i)%m;
	}
	for(int ans=1;ans<m;++ans){
		if(((ans*b)%m)==a){
			printf("%d",ans);
			return 0;
		}
	}
	return 0;
}

正解

计算C(N-K+1,K)mod M,跟方法三同样先计算出分子分母对M的余数a和b，根据x=(x/y)* y可知：a=(Ansb)mod m，再转化成Ans b+m* P=a，其中b,m和a为已知，并且m为素数，这样就变成我们熟悉的a* x+b* y=c，用扩展GCD来求。时间复杂度为O(N)。预计得分：100分。

代码（咕咕）

T4 逃离洞穴 100/40

题意

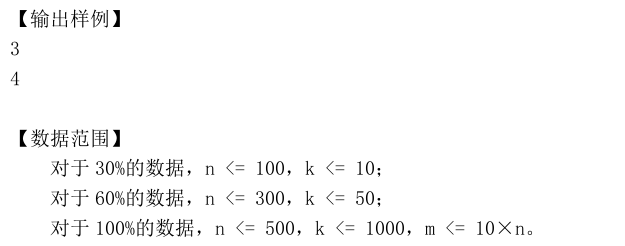
嘤嘤嘤，这题本来能ac的就差一点点啊，忘记判断有人的才取最大值了。。。
spfa还没死

代码

#include<bits/stdc++.h>
using namespace std;
inline int read(){
    int x=0,f=1;
    char ch=getchar();
    while(ch<'0'||ch>'9'){
        if(ch=='-')
            f=-1;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9'){
        x=(x<<1)+(x<<3)+(ch^48);
        ch=getchar();
    }
    return x*f;
}
const int N=510,M=100010;
int head[N],ver[M],edge[M],Next[M],d1[N],d2[N],d[N],op[N];
int n,m,k,T,tot,maxn;
queue<int> q;
bool v[N];
long long ans;
void add(int x,int y,int z){
	ver[++tot]=y;edge[tot]=z;Next[tot]=head[x],head[x]=tot;
}
void spfa(){
	memset(d1,0x3f,sizeof(d1));
	d1[1]=0,v[1]=1;
	q.push(1);
	while(q.size()){
		int x=q.front();q.pop();
		v[x]=0;
		for(int i=head[x];i;i=Next[i]){
			int y=ver[i],z=edge[i];
			if(d1[y]>d1[x]+z){
				d1[y]=d1[x]+z;
				if(!v[y]) q.push(y),v[y]=1;
			}
		}
	}
	memset(d2,0x3f,sizeof(d2));
	memset(v,0,sizeof(v));
	d2[n]=0,v[n]=1;
	q.push(n);
	while(q.size()){
		int x=q.front();q.pop();
		v[x]=0;
		for(int i=head[x];i;i=Next[i]){
			int y=ver[i],z=edge[i];
			if(d2[y]>d2[x]+z){
				d2[y]=d2[x]+z;
				if(!v[y]) q.push(y),v[y]=1;
			}
		}
	}
	for(int i=1;i<=n;++i){
		d[i]=min(d1[i],d2[i]);
	}
}
int main(){
	freopen("escape.in","r",stdin);
	freopen("escape.out","w",stdout);
	n=read();m=read();T=read();
	for(int i=1;i<=m;++i){
		int x,y,z;
		x=read();y=read();z=read();
		add(x,y,z);
		add(y,x,z);
	}
	spfa();
	k=read();
	int tmp;
	for(int i=1;i<=k;++i){
		tmp=read();
		op[tmp]++;
	}
	for(int i=1;i<=n;++i){
		if(d[i]<=T)  ans+=op[i];
		if(op[i]) maxn=max(maxn,min(d1[i],d2[i]));
	}
	printf("%lld
%d",ans,maxn);
	return 0;
}
/*
4 4 3
1 2 5
2 4 3
1 3 4
3 4 6
4
1 2 3 4
*/