第一眼看到这题,哇,这不是我刚做完的题吗?大水题!然后




这题表面很水,实际上有点坑。
题意
求经过 $ 1 - n $(不能遗漏) 并且回到 $ 1 $ 的最短路。
在看这题之前我们可以来看下这题
最短Hamilton路
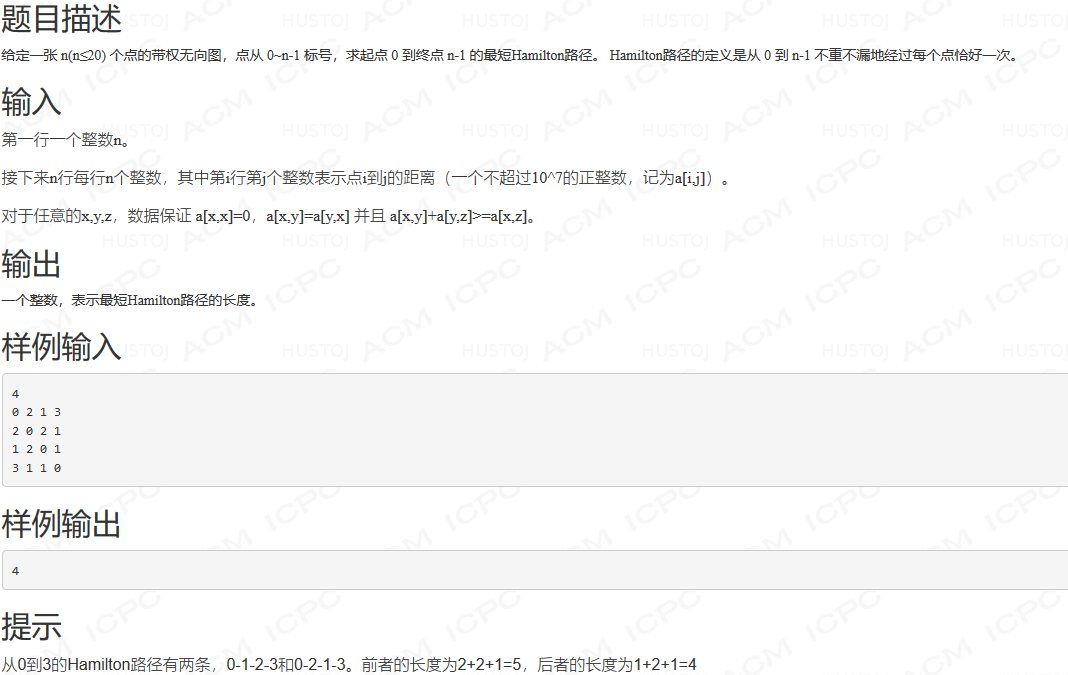
这道题的要求是我们要让每个点不重不漏的经过并且最终到达 $ n-1 $ 我们看数据范围,就可以直接状压dp,枚举状态。
由于题目已经给出最短路,便可以直接计算
#include<bits/stdc++.h>
using namespace std;
int n,a[30][30];
int f[1100000][30];
int main(){
scanf("%d",&n);
for(int i=0;i<n;++i){
for(int j=0;j<n;++j){
scanf("%d",&a[i][j]);
}
}
memset(f,0x3f,sizeof(f));
f[1][0]=0;
for(int i=1;i<(1<<n);++i){//状态
for(int j=0;j<n;++j){//终点
if((i>>j)&1){
for(int k=0;k<n;++k){//起点
if(((i>>k)&1)&&a[j][k]){//保证有路相通
f[i][j]=min(f[i][j],f[i^(1<<j)][k]+a[k][j]);//找没能达到j的
}
}
}
}
}
printf("%d",f[(1<<n)-1][n-1]);//最后在n-1
return 0;
}
那么我们回到这题,它给出每个点的边,最后都要经过,并且返回,仔细一想,不就是多了个最短路吗?直接跑一遍 $ floyd $ 枚举终点返回不就好了?
然后我就写下了这个代码
#include<bits/stdc++.h>
using namespace std;
const int INF=1<<30;
int n,m,T,dis[20][20];
int f[(1<<20)][20];
int main(){
scanf("%d",&T);
while(T--){
scanf("%d %d",&n,&m);
if(n==1){
printf("0
");
continue;
}
for(int i=1;i<=n;++i){
for(int j=1;j<=n;++j){
if(i==j) dis[i][j]=0;
else dis[i][j]=INF;
}
}
for(int i=1;i<=m;++i){
int x,y,z;
scanf("%d %d %d",&x,&y,&z);
dis[x][y]=min(dis[x][y],z);
dis[y][x]=dis[x][y];
}
for(int k=1;k<=n;++k){
for(int i=1;i<=n;++i){
for(int j=1;j<=n;++j){
if(dis[i][j]>dis[i][k]+dis[k][j]) dis[i][j]=dis[i][k]+dis[k][j];
}
}
}
memset(f,0x3f,sizeof(f));
f[1][1]=0;
for(int i=1;i<(1<<n);++i){
for(int j=1;j<=n;++j){
if((i>>(j-1))&1){
for(int k=1;k<=n;++k){
if(((i>>(k-1))&1)&&(dis[j][k]!=INF)){
f[i][j]=min(f[i][j],f[i^(1<<(j-1))][k]+dis[j][k]);
}
}
}
}
}
int ans=1<<30;
for(int i=1;i<=n;++i){
ans=min(ans,f[(1<<n)-1][i]+dis[i][1]);
}printf("%d
",ans);
}
return 0;
}
然后RE,后面问了乐老师,发现这个题会出现自环
if(n==1){
printf("0
");
continue;
}
这个就是问题的关键所在,不能直接 $ continue $ 因为后面还有边没读进来,会导致RE。
然后我就这样写了一下
#include<bits/stdc++.h>
using namespace std;
const int INF=1<<30;
int n,m,T,dis[20][20];
int f[(1<<20)][20];
int main(){
scanf("%d",&T);
while(T--){
scanf("%d %d",&n,&m);
for(int i=0;i<=n;++i){
for(int j=0;j<=n;++j){
if(i==j) dis[i][j]=0;
else dis[i][j]=INF;
}
}
for(int i=1;i<=m;++i){
int x,y,z;
scanf("%d %d %d",&x,&y,&z);
dis[x][y]=min(dis[x][y],z);
dis[y][x]=dis[x][y];
}
if(n==1){
printf("0");
continue;
}
for(int k=1;k<=n;++k){
for(int i=1;i<=n;++i){
for(int j=1;j<=n;++j){
if(dis[i][j]>dis[i][k]+dis[k][j]) dis[i][j]=dis[i][k]+dis[k][j];
}
}
}
memset(f,0x3f,sizeof(f));
f[1][1]=0;
for(int i=1;i<(1<<n);++i){
for(int j=1;j<=n;++j){
if((i>>(j-1))&1){
for(int k=1;k<=n;++k){
if(((i>>(k-1))&1)&&(dis[k][j]!=INF)){
f[i][j]=min(f[i][j],f[i^(1<<(j-1))][k]+dis[k][j]);
}
}
}
}
}
int ans=1<<30;
for(int i=1;i<=n;++i){
ans=min(ans,f[(1<<n)-1][i]+dis[i][1]);
}printf("%d
",ans);
}
return 0;
}
听取 $ wa $ 声一片,后面自己看了下题解,觉得思路没问题,看着它把最大值都定义为 $ 0x3f3f3f3f $ 我就一改,然后它过了??
原因是两个最大值不一样导致 $ dp $ 过程中会出现错误,最后我改成了
#include<bits/stdc++.h>
using namespace std;
const int INF=0x3f3f3f3f;
int n,m,T,dis[20][20];
int f[(1<<20)][20];
int main(){
scanf("%d",&T);
while(T--){
scanf("%d %d",&n,&m);
for(int i=0;i<=n;++i){
for(int j=0;j<=n;++j){
if(i==j) dis[i][j]=0;
else dis[i][j]=INF;
}
}
for(int i=1;i<=m;++i){
int x,y,z;
scanf("%d %d %d",&x,&y,&z);
dis[x][y]=min(dis[x][y],z);
dis[y][x]=dis[x][y];
}
if(n==1){
printf("0
");
continue;
}
for(int k=1;k<=n;++k){
for(int i=1;i<=n;++i){
for(int j=1;j<=n;++j){
if(dis[i][j]>dis[i][k]+dis[k][j]) dis[i][j]=dis[i][k]+dis[k][j];
}
}
}
memset(f,0x3f,sizeof(f));
f[1][1]=0;
for(int i=1;i<(1<<n);++i){
for(int j=1;j<=n;++j){
if((i>>(j-1))&1){
for(int k=1;k<=n;++k){
if(((i>>(k-1))&1)&&(dis[k][j]!=INF)){
f[i][j]=min(f[i][j],f[i^(1<<(j-1))][k]+dis[k][j]);
}
}
}
}
}
int ans=INF;
for(int i=1;i<=n;++i){
ans=min(ans,f[(1<<n)-1][i]+dis[i][1]);
}printf("%d
",ans);
}
return 0;
}
然后终于 $ AC $,其实这道题本身不难,主要是在一些细节上的处理,在多组数据下暴露的很明显,平时写题细节方面还是要多多注意。