深入浅出红黑树(Java TreeMap)

 实现原理:红黑树

什么是红黑树(数据来自百度百科):

    红黑树(自平衡二叉树)是每个节点都带有颜色属性的二叉查找树，颜色或红色或黑色。在二叉查找树强制一般要求以外，对于任何有效的红黑树我们增加了如下的额外要求:

性质1. 节点是红色或黑色。

性质2. 根节点是黑色。

性质3. 每个叶节点（NIL节点，空节点）是黑色的。

性质4. 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)

性质5. 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。

    这些约束强制了红黑树的关键性质: 从根到叶子的最长的可能路径不多于最短的可能路径的两倍长。结果是这个树大致上是平衡的。因为操作比如插入、删除和查找某个值的最坏情况时间都要求与树的高度成比例，这个在高度上的理论上限允许红黑树在最坏情况下都是高效的，而不同于普通的二叉查找树。

 

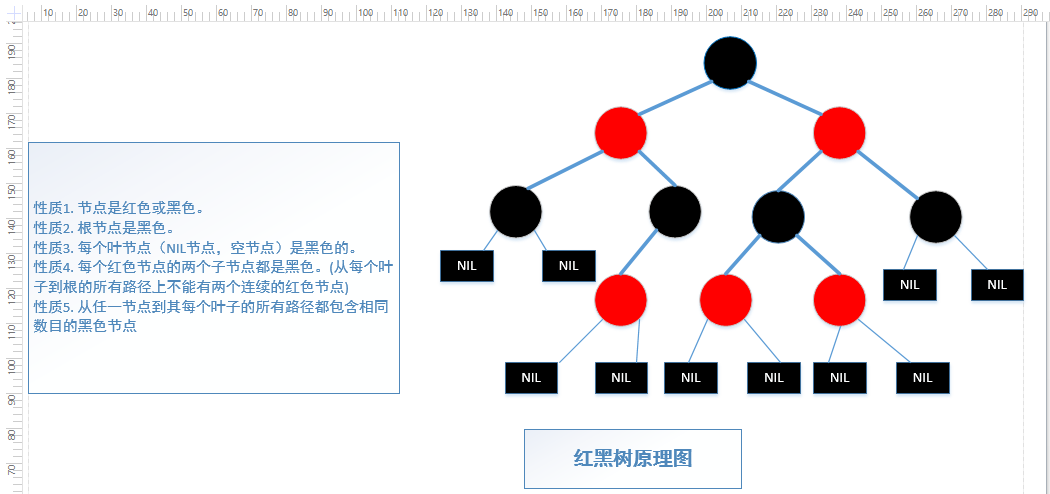
思路:

1.创建空比较器,空Entry引用,entry个数默认为0

 //比较器，因为TreeMap是有序的，通过comparator接口我们可以对TreeMap的内部排序进行精密的控制
 private final Comparator<? super K> comparator;
 //TreeMap红-黑节点，为TreeMap的内部类
 private transient Entry<K,V> root = null;
    
 private transient int size = 0;
 
 private static final boolean RED   = false;
 
 private static final boolean BLACK = true;

2.四个构造器,全部使用比较器,比较器基本容器/单位?

 public TreeMap() {
    comparator = null;
 }
 public TreeMap(Comparator<? super K> comparator) {
        this.comparator = comparator;
 }
 public TreeMap(Map<? extends K, ? extends V> m) {
        comparator = null;
        putAll(m);
 }
public TreeMap(SortedMap<K, ? extends V> m) {
        comparator = m.comparator();
        try {
            buildFromSorted(m.size(), m.entrySet().iterator(), null, null);
        } catch (java.io.IOException cannotHappen) {
        } catch (ClassNotFoundException cannotHappen) {
        }
}

 3.Entry类

static final class Entry<K,V> implements Map.Entry<K,V> {
        K key;
        V value;
        Entry<K,V> left;
        Entry<K,V> right;
        Entry<K,V> parent;
        boolean color = BLACK;
    
        /**
         * Make a new cell with given key, value, and parent, and with
         * {@code null} child links, and BLACK color.
         */
        Entry(K key, V value, Entry<K,V> parent) {
            this.key = key;
            this.value = value;
            this.parent = parent;
        }

    }

4.put方法

    两个点:

        构建一个有序二叉树

        平衡二叉树

 

1、以根节点为初始节点进行检索。

2、与当前节点进行比对，若新增节点值较大，则以当前节点的右子节点作为新的当前节点。

   否则以当前节点的左子节点作为新的当前节点。

3、循环递归2步骤知道检索出合适的叶子节点为止。

4、将新增节点与3步骤中找到的节点进行比对，如果新增节点较大，则添加为右子节点；否则添加为左子节点。

 

    1.root为空 

            新增根节点  

            return

    2.root不为空,比较器不为空,

            在root左右插入节点后 继续

            或者替换root值后     return

    3.root不为空,比较器为空

            key为空,抛出空指针

            在root左右插入节点后 继续

            或者替换root值后     return

public V put(K key, V value) {
        //用t表示二叉树的当前节点 
        Entry<K,V> t = root;
        //t为null表示一个空树，即TreeMap中没有任何元素，直接插入
        if (t == null) {
            //比较key值，个人觉得这句代码没有任何意义，空树还需要比较、排序？
            compare(key, key); // type (and possibly null) check
            //将新的key-value键值对创建为一个Entry节点，并将该节点赋予给root
            root = new Entry<>(key, value, null);
            //容器的size = 1，表示TreeMap集合中存在一个元素 
            size = 1;
            modCount++;
            return null;
        }
        //cmp表示key排序的返回结果
        int cmp;
        //父节点 
        Entry<K,V> parent;
        // split comparator and comparable paths
      //指定的排序算法 
        Comparator<? super K> cpr = comparator;
        //非空比较器时
        ////如果cpr不为空，则采用既定的排序算法进行创建TreeMap集合
        if (cpr != null) {
            do {
                //parent指向上次循环后的t
                parent = t;
                //比较新增节点的key和当前节点key的大小
                cmp = cpr.compare(key, t.key);
                //cmp返回值小于0，表示新增节点的key小于当前节点的key，
                //则以当前节点的左子节点作为新的当前节点
                if (cmp < 0)
                    t = t.left;
                //cmp返回值大于0，表示新增节点的key大于当前节点的key，
                //则以当前节点的右子节点作为新的当前节点
                else if (cmp > 0)
                    t = t.right;
                else //cmp返回值等于0，表示两个key值相等，则新值覆盖旧值，并返回新值
                    return t.setValue(value);
            } while (t != null);
        }
        else { //如果cpr为空，则采用默认的排序算法进行创建TreeMap集合
            //key不能为空
            if (key == null)
                throw new NullPointerException();
            /* 下面处理过程和上面一样 */
            @SuppressWarnings("unchecked")
                Comparable<? super K> k = (Comparable<? super K>) key;
            do {
                parent = t;
                cmp = k.compareTo(t.key);
                if (cmp < 0)
                    t = t.left;
                else if (cmp > 0)
                    t = t.right;
                else
                    return t.setValue(value);
            } while (t != null);
        }
        //将新增节点当做parent的子节点
        Entry<K,V> e = new Entry<>(key, value, parent);
       //如果新增节点的key小于parent的key，则当做左子节点  
        if (cmp < 0)
            parent.left = e;
        else    //如果新增节点的key大于parent的key，则当做右子节点
            parent.right = e;
    
         /**
         *  上面已经完成了排序二叉树的的构建，将新增节点插入该树中的合适位置             
         *  下面fixAfterInsertion()方法就是对这棵树进行调整、平衡，具体过程参考上面的五种情况                  */ 
        fixAfterInsertion(e);
        size++;
        modCount++;
        return null;
    }

　上面的do{}代码仅仅是排序二叉树的核心算法,真正的实现红黑树依靠的是fixAfterInsertion(e)方法 

    红黑树是一棵平衡排序二叉树，普通的排序二叉树可能会出现失衡的情况,而fixAfterInsertion就是调      整结构实现红黑树 : 左旋、右旋、着色三个基本操作 

/** From CLR */
    private void fixAfterInsertion(Entry<K,V> x) {
        //新节点着色
        x.color = RED;
        //循环到新节点 不为空且不是根且根的节点不是红色
        while (x != null && x != root && x.parent.color == RED) {
         
            //如果X的父节点（假设为:P）是其父节点的父节点（假设为:G）的左节点
            if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {
                //获取父节点的父节点的右节点y
                Entry<K,V> y = rightOf(parentOf(parentOf(x)));
       //         G
       //       /   
       //     p       y
       //    / 
       //   x       
                if (colorOf(y) == RED) {
                    setColor(parentOf(x), BLACK);
                    setColor(y, BLACK);
                    setColor(parentOf(parentOf(x)), RED);
                    // ?????
                    x = parentOf(parentOf(x));
                } else {
                    //右旋
                    if (x == rightOf(parentOf(x))) {
                        x = parentOf(x);
                        //以X的父节点的父节点（G）为中心左旋转
                        rotateLeft(x);
                    }
                    setColor(parentOf(x), BLACK);
                    setColor(parentOf(parentOf(x)), RED);
                    rotateRight(parentOf(parentOf(x)));
                }
            } else {
                //如果X的父节点（假设为:P）是其父节点的父节点（假设为:G）的右节点
                //                G
                //              /   
                //             y     P
                //                    
                //                     x
                //
                
                Entry<K,V> y = leftOf(parentOf(parentOf(x)));
                if (colorOf(y) == RED) {
                    setColor(parentOf(x), BLACK);
                    setColor(y, BLACK);
                    setColor(parentOf(parentOf(x)), RED);
                    x = parentOf(parentOf(x));
                } else {
                    //左旋
                    if (x == leftOf(parentOf(x))) {
                        x = parentOf(x);
                        //以X的父节点的父节点（G）为中心右旋转
                        rotateRight(x);
                    }
                    setColor(parentOf(x), BLACK);
                    setColor(parentOf(parentOf(x)), RED);
                    rotateLeft(parentOf(parentOf(x)));
                }
            }
        }
        root.color = BLACK;
    }

右旋方法(左旋类似)

/** From CLR */
    private void rotateRight(Entry<K,V> p) {
        if (p != null) {
            //    p
            //   /
            //   L
            //将L设置为P的左子树
            Entry<K,V> l = p.left;
            //将L的右子树设置为P的左子树
            p.left = l.right;
             //若L的右子树不为空，则将P设置L的右子树的父节点
            if (l.right != null) l.right.parent = p;
            //将P的父节点设置为L的父节点
            l.parent = p.parent;
             //如果P的父节点为空，则将L设置根节点 
            if (p.parent == null)
                root = l;
            //若P为其父节点的右子树，则将L设置为P的父节点的右子树
            else if (p.parent.right == p)
                p.parent.right = l;
            //否则将L设置为P的父节点的左子树
            else p.parent.left = l;
            //将P设置为L的右子树
            l.right = p;
            //将L设置为P的父节点
            p.parent = l;
        }
    }