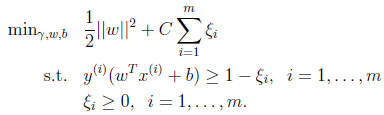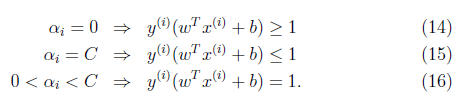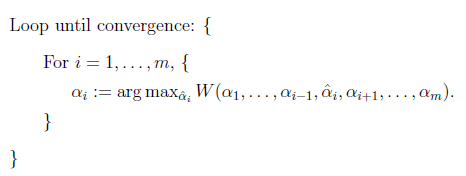9 规则化和不可分情况处理(Regularization and the non-separable case)
我们之前讨论的情况都是建立在样例线性可分的假设上,当样例线性不可分时,我们可以尝试使用核函数来将特征映射到高维,这样很可能就可分了。然而,映射后我们也不能100%保证可分。那怎么办呢,我们需要将模型进行调整,以保证在不可分的情况下,也能够尽可能地找出分隔超平面。
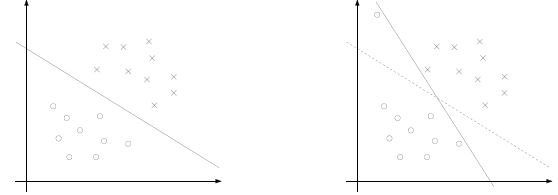
看下面两张图:
可以看到一个离群点(可能是噪声)可以造成超平面的移动,间隔缩小,可见以前的模型对噪声非常敏感。再有甚者,如果离群点在另外一个类中,那么这时候就是线性不可分了。
这时候我们应该允许一些点游离并在在模型中违背限制条件(函数间隔大于1)。我们设计得到新的模型如下(也称软间隔):
引入非负参数![]() 后(称为松弛变量),就允许某些样本点的函数间隔小于1,即在最大间隔区间里面,或者函数间隔是负数,即样本点在对方的区域中。而放松限制条件后,我们需要重新调整目标函数,以对离群点进行处罚,目标函数后面加上的
后(称为松弛变量),就允许某些样本点的函数间隔小于1,即在最大间隔区间里面,或者函数间隔是负数,即样本点在对方的区域中。而放松限制条件后,我们需要重新调整目标函数,以对离群点进行处罚,目标函数后面加上的![]() 就表示离群点越多,目标函数值越大,而我们要求的是尽可能小的目标函数值。这里的C是离群点的权重,C越大表明离群点对目标函数影响越大,也就是越不希望看到离群点。我们看到,目标函数控制了离群点的数目和程度,使大部分样本点仍然遵守限制条件。
就表示离群点越多,目标函数值越大,而我们要求的是尽可能小的目标函数值。这里的C是离群点的权重,C越大表明离群点对目标函数影响越大,也就是越不希望看到离群点。我们看到,目标函数控制了离群点的数目和程度,使大部分样本点仍然遵守限制条件。
模型修改后,拉格朗日公式也要修改如下:
这里的![]() 和
和![]() 都是拉格朗日乘子,回想我们在拉格朗日对偶中提到的求法,先写出拉格朗日公式(如上),然后将其看作是变量w和b的函数,分别对其求偏导,得到w和b的表达式。然后代入公式中,求带入后公式的极大值。整个推导过程类似以前的模型,这里只写出最后结果如下:
都是拉格朗日乘子,回想我们在拉格朗日对偶中提到的求法,先写出拉格朗日公式(如上),然后将其看作是变量w和b的函数,分别对其求偏导,得到w和b的表达式。然后代入公式中,求带入后公式的极大值。整个推导过程类似以前的模型,这里只写出最后结果如下:
此时,我们发现没有了参数![]() ,与之前模型唯一不同在于
,与之前模型唯一不同在于![]() 又多了
又多了![]() 的限制条件。需要提醒的是,b的求值公式也发生了改变,改变结果在SMO算法里面介绍。先看看KKT条件的变化:
的限制条件。需要提醒的是,b的求值公式也发生了改变,改变结果在SMO算法里面介绍。先看看KKT条件的变化:
第一个式子表明在两条间隔线外的样本点前面的系数为0,离群样本点前面的系数为C,而支持向量(也就是在超平面两边的最大间隔线上)的样本点前面系数在(0,C)上。通过KKT条件可知,某些在最大间隔线上的样本点也不是支持向量,相反也可能是离群点。
10 坐标上升法(Coordinate ascent)
在最后讨论![]() 的求解之前,我们先看看坐标上升法的基本原理。假设要求解下面的优化问题:
的求解之前,我们先看看坐标上升法的基本原理。假设要求解下面的优化问题:
这里W是![]() 向量的函数。之前我们在回归中提到过两种求最优解的方法,一种是梯度下降法,另外一种是牛顿法。现在我们再讲一种方法称为坐标上升法(求解最小值问题时,称作坐标下降法,原理一样)。
向量的函数。之前我们在回归中提到过两种求最优解的方法,一种是梯度下降法,另外一种是牛顿法。现在我们再讲一种方法称为坐标上升法(求解最小值问题时,称作坐标下降法,原理一样)。
方法过程:
最里面语句的意思是固定除![]() 之外的所有
之外的所有![]() ,这时W可看作只是关于
,这时W可看作只是关于![]() 的函数,那么直接对
的函数,那么直接对![]() 求导优化即可。这里我们进行最大化求导的顺序i是从1到m,可以通过更改优化顺序来使W能够更快地增加并收敛。如果W在内循环中能够很快地达到最优,那么坐标上升法会是一个很高效的求极值方法。
求导优化即可。这里我们进行最大化求导的顺序i是从1到m,可以通过更改优化顺序来使W能够更快地增加并收敛。如果W在内循环中能够很快地达到最优,那么坐标上升法会是一个很高效的求极值方法。
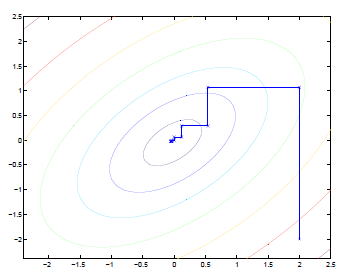
下面通过一张图来展示:
椭圆代表了二次函数的各个等高线,变量数为2,起始坐标是(2,-2)。图中的直线式迭代优化的路径,可以看到每一步都会向最优值前进一步,而且前进路线是平行于坐标轴的,因为每一步只优化一个变量。