一.基础数学知识
1.数列求和
等差数列求和:Sn=n(a1+an)/2
等比数列求和: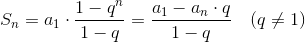
无穷级数:等比求和 q(公比)<1,结果为 1/1-q.
二.递归方程有关问题
1.如何归纳一个算法
要了解这个算法的步骤,再根据实际的时间进行归纳。
例:hanoi塔,n!,合并排序算法,finbo。
hanoi塔的具体算法:
hanoi(int n,char from,char by,char to )
{
if(n==1) printf("%c->%c",from,to);// T(n) : n==1 时 O(1)
else // n>1时,T(n)= 2*T(n-1) +1
{
hanoi(n-1,from,to,by);
printf("%c->%c",from,to);
hanoi(n-1,by,from,to);
}
}
N!的算法:
int jc(int n)
{
if(n==0) return 0; //n==0时 O(1);
else
return n*jc(n-1); //n>1时 T(n-1) + 1; T(n)=T(n-1)+1
}
Fibonacci:
int Fibonacci(int n)
{
if (n==0) return 0; //n==0, O(1)
if(n==1) return 1; //n==1,O(1)
else
return Fibonacci(n-1)+Fibonacci(n-2); // n>1 T(n-1)+T(n-2)+O(1) T(n)=T(n-1)+T(n-2)+1;
}
2.递归方程的求解方法
2.1 如果f(n)不为一阶,如下:
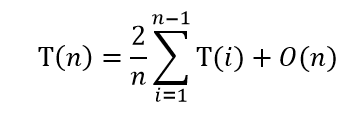
可采用 差消法:先将其划为一阶再进行求解。如下:
nT(n) = 2ΣT(i)+c1n*2
n-1T(n-1) = 2ΣT(i-1)+c1(n-1)*2
nT(n)-(n-1)T(n-1)=2T(n-1)+c1(n*2-(n-1)*2)
T(n)/n+1=T(n-1)/n+c1/n+1
利用迭代法:T(n) = Θ(nlogn)
2.2如果F(n)为一阶,则求解方法如下:
1.迭代法
例:T(n)= 2*T(n-1) +1 (T(1)=0)
T(n)=2*[2*T(n-2)+1]+1
......
T(n)=2*(n-1)T(1)+2*0+2*1+....+2*(n-1)
T(n)=2*n-1=O(2*n)
2.母函数法
例: F(n)=F(n-1)+F(n-2)
x*n-x*(n-1)-x*(n-2)=0 //同时除以x*(n-2)
x*2-x-1=0
x1=(1+根号下5 )/2,x2= -根号下5/2;
F(n)=c1(x1)+c2(x2)
F(n)=O(x1)*n
3.递归树法
例:
T(n)=aT(n/b)+f(n)
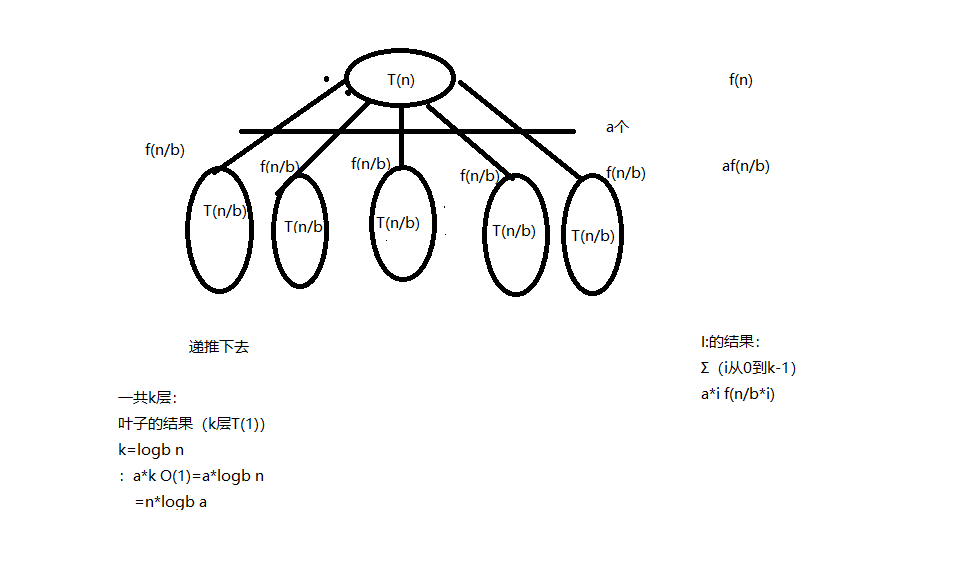
比较 n*logb a 与 a*i f(n/b*i) 可得到主定理
4.主定理法


