一、题目
给定一个十进制的正整数,写下从1开始,到N的所有整数,然后数一下其中出现“1”的个数。
要求:
写一个函数 f(N) ,返回1 到 N 之间出现的 “1”的个数。例如 f(12) = 5。
在32位整数范围内,满足条件的“f(N) =N”的最大的N是多少。
二、设计思路
起初自己可以实现的思路是遍历每个数对10求余看是否等于1来统计,但时间复杂度高,不是最优算法。
另一种较优算法是分析正整数N各个位置上1出现的个数,即它的个位、十位、百位……上1的个数。先寻找规律:
f(13)=2+4=6
f(23)=3+10=13
f(33)=4+10=14
f(93)=10+10=20
……
结论是某一位上1的个数与其位上的数字、其高一位上的数字、其低一位上的数字数字有关,具体规则在代码注释中写出。将各位上1的个数相加即得结果。
三、代码
1 #include<iostream.h> 2 3 int Count(int n) 4 { 5 int count=0; //对1的个数计数 6 int now=1; //N由最低位到最高位此时对应第now位 7 int l=0; //第now位的低一位的数字 8 int nownum=0; //第now位的数字 9 int h=0; //第now位的高一位的数字 10 if(n<=0) 11 { 12 return 0; 13 } 14 while(n/now!=0) 15 { 16 l=n-(n/now)*now; 17 nownum=(n/now)%10; 18 h=n/(now*10); 19 if(nownum==0) //第now位的数字为0时,1的个数等于第now位的高一位的数字*now 20 { 21 count+=h*now; 22 } 23 else if(nownum==1)//第now位的数字为1时,1的个数等于第now位的高一位的数字*now在加1 24 { 25 count+=h*now+l+1; 26 } 27 else//第now位的数字大于1时,1的个数等于(第now位的高一位的数字+1)*now 28 { 29 count+=(h+1)*now; 30 } 31 now*=10; //第now位指向他的高一位 32 } 33 return count; 34 } 35 36 int main() 37 { 38 int a; 39 cout<<"请输入正整数N:"<<endl; 40 cin>>a; 41 cout<<"f("<<a<<")="<<Count(a)<<endl; 42 return 0; 43 }
四、运行结果截图
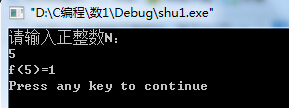

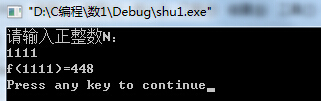
五、总结
这道题老师所给的思路大致清楚,但没有得到结果,也未能实现代码。这是找的核心代码理解后修改参数完整实现的,但寻找满足条件的“f(N) =N”的最大的N还不会。自己在找最优算法上还需要提高。