洛谷P3941入阵曲

洛谷P3941入阵曲

【题目描述】

　　丹青千秋酿，一醉解愁肠。 无悔少年枉，只愿壮志狂。

小 F 很喜欢数学，但是到了高中以后数学总是考不好。 有一天，他在数学课上发起了呆；他想起了过去的一年。一年前，当他初识算法竞赛的 时候，觉得整个世界都焕然一新。这世界上怎么会有这么多奇妙的东西？曾经自己觉得难以 解决的问题，被一个又一个算法轻松解决。 小 F 当时暗自觉得，与自己的幼稚相比起来，还有好多要学习的呢。 一年过去了，想想都还有点恍惚。 他至今还能记得，某天晚上听着入阵曲，激动地睡不着觉，写题写到鸡鸣时分都兴奋不 已。也许，这就是热血吧。 

 

也就是在那个时候，小 F 学会了矩阵乘法。让两个矩阵乘几次就能算出斐波那契数列的 第 10^100 项，真是奇妙无比呢。 不过，小 F 现在可不想手算矩阵乘法——他觉得好麻烦。取而代之的，是一个简单的小 问题。他写写画画，画出了一个 × 的矩阵，每个格子里都有一个不超过 的正整数。 小 F 想问问你，这个矩阵里有多少个不同的子矩形中的数字之和是 的倍数？ 如果把一个子矩形用它的左上角和右下角描述为 (1,1,2,2)，其中1 ≤ 2,1 ≤ 2； 那么，我们认为两个子矩形是不同的，当且仅当他们以 (1,1,2,2) 表示时不同；也就是 说，只要两个矩形以 (1,1,2,2) 表示时相同，就认为这两个矩形是同一个矩形，你应该 在你的答案里只算一次。 

【输入格式】

　　 从文件 rally.in 中读入数据。 输入第一行，包含三个正整数 ,,。 输入接下来 行，每行包含 个正整数，第 行第 列表示矩阵中第 行第 列 中所填的正整数 ,。 

【输出格式】

　　输出到文件 rally.out 中。 输入一行一个非负整数，表示你的答案。 

【样例 1 输入】

　　2 3 2

　　1 2 1

　　2 1 2 

【样例 1 输出】

　　 6 
【样例 1 说明】

　　 这些矩形是符合要求的： (1, 1, 1, 3)，(1, 1, 2, 2)，(1, 2, 1, 2)，(1, 2, 2, 3)，(2, 1, 2, 1)，(2, 3, 2, 3)。 

【样例 2】

　　 见选手目录下的 rally/rally2.in 与 rally/rally2.ans 。


【数据范围与约定】

　　子任务会给出部分测试数据的特点。如果你在解决题目中遇到了困难，可以尝试只解 决一部分测试数据。 每个测试点的数据规模及特点如下表： 

　　

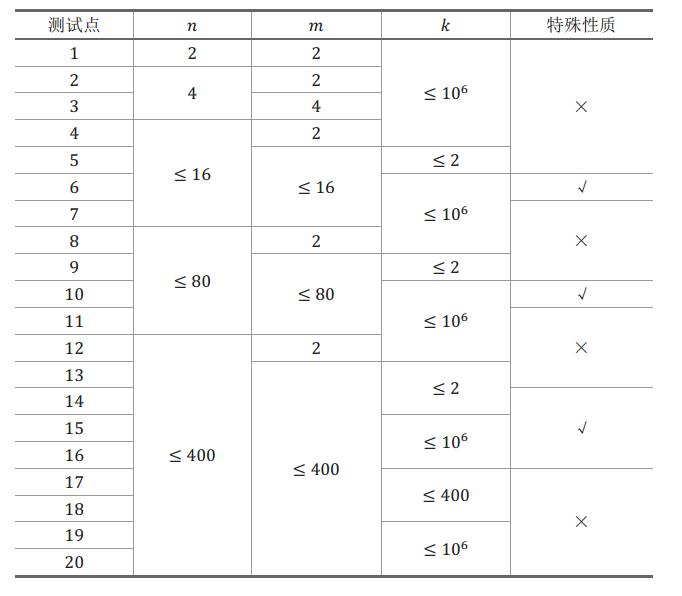
          特殊性质：保证所有 , 均相同。

看到这道题，我想到了前几天做的牛宫，给定宽的上下界，再枚举长，看该矩阵和是否为k的倍数（当然不可能暴枚举），

易发现，若有两个矩阵和除以k的余数相同，那么这两个矩阵和相减必定为k的倍数。

也就是说，只要子矩阵模k下的余数出现两次，那么该矩阵必定包含一个为k的倍数的矩阵。

所以处理出前缀和模k，统计情况即可。

#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;
int n,m,mod;
long long a[401][401];
int s[4010][4010],f[2222222],sum[2222222];
long long ans;
int main()
{
   scanf("%d%d%d",&n,&m,&mod);
   for(int i=1;i<=n;i++)
   for(int j=1;j<=m;j++)
   {
     scanf("%lld",&a[i][j]);
     s[i][j]=(s[i][j-1]+s[i-1][j]-s[i-1][j-1]+a[i][j])%mod;
   }
   for(int i=0;i<n;++i)
   for(int j=i+1;j<=n;++j)
   {
     f[0]=1;
     for(int k=1;k<=m;++k)
     {
         sum[k]=((s[j][k]-s[i][k])%mod+mod)%mod;//防止出现负数 
         ans+=f[sum[k]]; 
         f[sum[k]]++; 
     }
     for(int k=1;k<=m;++k)
     f[sum[k]]=0;
   }
  cout<<ans<<endl;
  return 0;
}