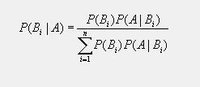简介
学过概率理论的人都知道条件概率的公式:P(AB)=P(A)P(B|A)=P(B)P(A|B);即事件A和事件B同时发生的概率等于在发生A的条件下B发生的概率乘以A的概率。由条件概率公式推导出贝叶斯公式:P(B|A)=P(A|B)P(B)/P(A);即,已知P(A|B),P(A)和P(B)可以计算出P(B|A)。
假设B是由相互独立的事件组成的概率空间{B1,b2,...bn}。则P(A)可以用全概率公式展开:P(A)=P (A|B1)P(B1)+P(A|B2)P(B2)+..P(A|Bn)P(Bn)。贝叶斯公式表示成:P(Bi|A)=P(A|Bi)P(Bi)/(P(A|B1)P(B1)+P(A|B2)P(B2)+..P(A|Bn)P(Bn));常常把P(Bi|A)称作后验概率,而P(A|Bn)P(Bn)为先验概率。而P(Bi)又叫做基础概率。
贝叶斯公式:
贝叶斯公式看起来很简单,但是在自然科学领域应用范围及其广泛。同时理论本身蕴含了深刻的思想。
贝叶斯概率的历史
贝叶斯理论和贝叶斯概率以托马斯·贝叶斯(1702-1761)命名,他证明了现在称为贝叶斯定理的一个特例。术语贝叶斯却是在1950年左右开始使用,很难说贝叶斯本人是否会支持这个以他命名的概率非常广义的解释。拉普拉斯证明了贝叶斯定理的一个更普遍的版本,并将之用于解决天体力学、医学统计中的问题,在有些情况下,甚至用于法理学。但是拉普拉斯并不认为该定理对于概率论很重要。他还是坚持使用了概率的经典解释。
弗兰克·普伦普顿·拉姆齐在《数学基础》(1931年)中首次建议将主观置信度作为概率的一种解释。Ramsey视这种解释为概率的频率解释的一个补充,而频率解释在当时更为广泛接受。统计学家Bruno de Finetti于1937年采纳了Ramsey的观点,将之作为概率的频率解释的一种可能的代替。L. J. Savage在《统计学基础》(1954年)中拓展了这个思想。
有人试图将“置信度”的直观概念进行形式化的定义和应用。最普通的应用是基于打赌:置信度反映在行为主体愿意在命题上下注的意愿上。
当信任有程度的时候,概率计算的定理测量信任的理性程度,就像一阶逻辑的定理测量信任的理性程度一样。很多人将置信度视为经典的真值(真或假)的一种扩展。
Harold Jeffreys, Richard T. Cox, Edwin Jaynes和I. J. Good研探了贝叶斯理论。其他著名贝叶斯理论的支持者包括John Maynard Keynes和B.O. Koopman。
贝叶斯法则的原理
通常,事件A在事件B(发生)的条件下的概率,与事件B在事件A的条件下的概率是不一样的;然而,这两者是有确定的关系,贝叶斯法则就是这种关系的陈述。
作为一个规范的原理,贝叶斯法则对于所有概率的解释是有效的;然而,频率主义者和贝叶斯主义者对于在应用中概率如何被赋值有着不同的看法:频率主义者根据随机事件发生的频率,或者总体样本里面的个数来赋值概率;贝叶斯主义者要根据未知的命题来赋值概率。一个结果就是,贝叶斯主义者有更多的机会使用贝叶斯法则。
贝叶斯法则是关于随机事件A和B的条件概率和边缘概率的。
bayes&
其中L(A|B)是在B发生的情况下A发生的可能性。
在贝叶斯法则中,每个名词都有约定俗成的名称:
Pr(A)是A的先验概率或边缘概率。之所以称为"先验"是因为它不考虑任何B方面的因素。
Pr(A|B)是已知B发生后A的条件概率,也由于得自B的取值而被称作A的后验概率。
Pr(B|A)是已知A发生后B的条件概率,也由于得自A的取值而被称作B的后验概率。
Pr(B)是B的先验概率或边缘概率,也作标准化常量(normalized constant)。
按这些术语,Bayes法则可表述为:
后验概率 = (似然度 * 先验概率)/标准化常量 也就是说,后验概率与先验概率和似然度的乘积成正比。
另外,比例Pr(B|A)/Pr(B)也有时被称作标准似然度(standardised likelihood),Bayes法则可表述为:
后验概率 = 标准似然度 * 先验概率
要理解贝叶斯推断,必须先理解贝叶斯定理。后者实际上就是计算"条件概率"的公式。
所谓"条件概率"(Conditional probability),就是指在事件B发生的情况下,事件A发生的概率,用P(A|B)来表示。

根据文氏图,可以很清楚地看到在事件B发生的情况下,事件A发生的概率就是P(A∩B)除以P(B)。
因此,
同理可得,
所以,
即
这就是条件概率的计算公式。
全概率公式
由于后面要用到,所以除了条件概率以外,这里还要推导全概率公式。
假定样本空间S,是两个事件A与A'的和。

上图中,红色部分是事件A,绿色部分是事件A',它们共同构成了样本空间S。
在这种情况下,事件B可以划分成两个部分。

即
在上一节的推导当中,我们已知
所以,
这就是全概率公式。它的含义是,如果A和A'构成样本空间的一个划分,那么事件B的概率,就等于A和A'的概率分别乘以B对这两个事件的条件概率之和。
将这个公式代入上一节的条件概率公式,就得到了条件概率的另一种写法:
贝叶斯推断的含义
对条件概率公式进行变形,可以得到如下形式:
我们把P(A)称为"先验概率"(Prior probability),即在B事件发生之前,我们对A事件概率的一个判断。P(A|B)称为"后验概率"(Posterior probability),即在B事件发生之后,我们对A事件概率的重新评估。P(B|A)/P(B)称为"可能性函数"(Likelyhood),这是一个调整因子,使得预估概率更接近真实概率。
所以,条件概率可以理解成下面的式子:
后验概率 = 先验概率 x 调整因子
这就是贝叶斯推断的含义。我们先预估一个"先验概率",然后加入实验结果,看这个实验到底是增强还是削弱了"先验概率",由此得到更接近事实的"后验概率"。
在这里,如果"可能性函数"P(B|A)/P(B)>1,意味着"先验概率"被增强,事件A的发生的可能性变大;如果"可能性函数"=1,意味着B事件无助于判断事件A的可能性;如果"可能性函数"<1,意味着"先验概率"被削弱,事件A的可能性变小。
医患诊断模型
1、背景材料及引言
7岁女孩晓宇(化名)患急性支气管炎,在武汉市儿童医院住院4天,医生为确诊病情,为她抽血化验了32个指标,仅化验费就花费1130元。晓宇的家长质疑:医院如此看病,是过度检查。晓宇的接诊医生李志超说:“晓宇入院时,根据其家长自述病情,我认为孩子的情况有些严重,于是确定了上述化验指标”。该院四内科副主任李医生说:在当时情况下,李志超对患者的病情判断、以及开出的化验指标,都是有道理的。但如果是我接诊,会以自己的经验有针对性地进行化验检查,可能不会一下开出这么多化验指标。该科主任温玟莉主任医师称:一次抽血化验32个指标,是因为李志超当时怀疑孩子得了败血症,这样处理没有问题。但最后的检查结果并不是败血症,这只能说明李志超较年轻,缺乏丰富的临床经验,只有通过全面检查才能确诊。
在医患关系紧张,看病难、看病贵的现实情况下,我们应如何看待这个颇有争议的案例,医生看病是应该有针对性地开方,还是列出“算法式”的化验指标进行排查,本研究以贝叶斯公式为依据,从中国现行的医疗体制出发,对此类问题进行了有益的探索,以期建立一种定量化的诊断模型。
2、模型建立
设“患者有某种病症”为事件A,引起事件A的病因为样本空间Ω。B1,B2,…Bn为Ω的一个分划,即Bi∩Bj=Φ,i≠j,Uni=1Bi=Ω,并假定P(Bi)>0。由贝叶斯公式,由某病因引起事件A的概率为:
P(Bi|A)=P(Bi)P(A|Bi)/�n/j=1P(Bj)P(A⌒Bj)(1)
公式(1)为医生有针对性地确诊提供了参考。
在疹疗过程中,医生要根据临床经验对各种病因Bi进行权衡。如果误诊,则有可能承担相应的医疗事故风险,相应的误诊概率记为P′(Bi),并设因可能承担风险而承担的赔偿费用为C′i,患者承担医生针对病因Bi开出的疹疗方案的费用为Ci,于是在一次诊治过程中患者承担的平均费用为:
E(A)=�ni=1P(Bi)Ci(2)
医生可能承担的平均赔偿金额为:
E′(A)=�ni=1P′(Bi)C′i(3)
我们称该模型为诊断模型,并以δ1≤E(A)-E′(A)≤δ2为标准来衡量诊断方案的合理性,其中δ1≥0,δ2为某一不是特别大的正数。即患者所承担的平均医疗费用应比医生可能承担的平均赔偿金要多,但两者不应差别太大。
3、模型检验
我们以发热和上腹疼痛两个病症的相关数据对该模型进行检验。设原假设为H0:诊断是合理的。备择假设为H1,诊断合理与否需要进一步考查。
对表1和表2中相关数据的说明:中国2002年9月1日实施的《医疗事故处理条例》(以下简称《条例》)第五十条对赔偿项目和标准的规定与当地上一年度职工平均工资水平紧密挂钩,实行一次性结算。表1和表2中的工资水平参考了2007年2月湖北省第十届人民代表大会上的湖北省政府工作报告中的数据:2006年城镇居民人均可支配收入为9803元。对发热症状中的“非典”及“某种类似非典的突发疾病”所可能带来的医疗事故我们以一级医疗事故中的死亡来处理,赔偿金额按<国家赔偿法>第二十七条的规定,检查费用以一次全身检查所需费用10000元进行计算;对“心肺功能缺陷”所可能带来的医疗事故我们按二级医疗事故处理,赔偿金额取202110,检查费用按心电图20元次,心脏彩超180元次,心肌酶谱60元次,肺检查80元次进行计算,药费以相应检查费用的0.8计算。对上腹疼痛症状中的“胃癌”及“心、膈等器官有病变”可能带来的医疗事故我们按二级医疗事故来处理,赔偿金额取202110,对B3的检查费用以B超40元次,催C120元次,胃镜(无痛)240元次进行计算,药费以相应检查费用的0.8计算,对B4的检查费用以胃镜(无痛)240元次和心脏彩超180元次进行计算,药费以相应检查费用的0.8计算。对两种症状中“其它”原因对患者可能造成的损害我们以《条例》第三十三条(三)的规定进行处理:在现有医学科学技术条件下,发生无法预料或者不能防范的不良后果的,不属于医疗事故。对两种症状中“其它”原因,患者的一次医疗费用我们取城镇居民人均可支配收入的5%,即490元进行计算。所有医疗费用均指一次诊治的检查费和药费之和,不包括后续治疗的费用。检查费用以武汉市某三级甲等医院的相关标准为参考。表1发热症状诊断模型的相关数据注:B1=人体生理功能的正常表现:B4=某种类似非典的突发疾病;B5=心肺功能缺陷。表2上腹疼痛症状诊断模型的相关数据注,B2=胃溃疡、十二指肠溃疡;B4=心、膈等器官有病变。
设“发热症状”为事件A1,“上腹疼痛症状”为事件A2,由表1和表2的数据计算得(四舍五入精确到元):
E(A1)=121,E′(A1)=187165;E(A2)=265,E′(A2)=22232
我们会发现原假设H0:诊断是合理的,是不成立的。这些数据告诉我们医生这个职业的确是个高风险的职业,在中国建立医疗责任保险制度有着必要性与迫切性。
4、模型评价
该模型在合理假设的基础上,对“对症下药”进行量化,对诊疗方案的合理性给出了一个量化的标准,有一定的合理性与临床参考价值。特别是在用数据对模型检验后,证实了医生的确是个高风险的职业,也显示了在中国建立医疗责任保险制度的必要性和紧迫性。但在模型应用过程中还需要注意以下几个方面:①病因的复杂性。病因的复杂性会导致样本空间的分划的个数n比较大,因此需要结合医学规律对样本空间分划进行合理的选择。②患者体质的差别。不同的患者对同类的医疗事故,由于体质的差别可能带来不同程度的损害。③医生临床诊断水平的差异。不同的医生,由于经验等方面的因素,误诊概率可能有较大的差别。④医院的潜规则。有的医院把医生的收入与其给医院的创收挂钩,这样同一病症在不同的医院治疗,诊疗费用会有较大的差别。⑤实际赔偿金的差别。不同地区上一年度人均收入差别较大,加之实际赔偿金还与实际谈判能力有关系,这样就可能导致同类医疗事故在不同地区及不同的患者(或家属)身上,实际赔偿金差别也较大。⑥现行医疗体制对模型的影响。下面对此进行较详细的分析。
中国现行的医疗事故赔偿责任者只有一个,就是医疗机构,但医疗机构作为理性人,会尽量减少其自身的医疗成本以实现利益的最大化。医疗机构会将其自身受到的损失通过以下三种主要方式进行转移:一是利用价格机制,提高医疗费用,即将损失分散于所有的就医者身上;二是由具体责任人承担风险,即将损失的一部分转移给与事故直接相关的医务人员;三是通过责任保险机制,将损失转移给保险公司。但长期以来,在中国实际上只有第一种和第二种途径在发挥着作用,责任保险机制可以说作用甚微。
这样,就很容易导致医疗费用上涨,引发医患关系紧张。医学的专业化使得医疗机构和患者之间存在巨大的信息差,医疗机构有动机也有能力通过使患者进行重复或者不必要的检查项目等方法多收费用,弥补自身损失.因此模型作用的发挥,还需要以下几方面的配合:
①重视医德建设,提高医护人员自身修养。裘法祖院士在文献里有很深刻的认识。
②加强医患之间的沟通,进行换位思考,让医生理解患者的苦衷,让患者理解诊疗的风险。
③加强误诊规律的研究。医疗技术的进步从来都是和风险相并存的,从某种程度上说误诊是不可避免的,但作为医护人员要提高生命权保护意识,不断提高自身的临床思维能力诊断能力力争把误诊率降到最低。
④加强医护人员临床思维能力和临床经验的提高。医学很大程度上是经验学科,医学理论最终还要内化为医护人员的实际诊断能力才能发挥作用。公式(1)为医护人员提高诊断水平提供了一个很好的参考。
⑤探索适合中国国情的、于患于医均有益的医疗责任保险制度。尤其是在生命意识越来越受到重视的今天,只有切实的降低行医的风险,才能从根本上解决医患关系紧张的现状,实现医患关系的和谐。
别墅和狗
一座别墅在过去的 20 年里一共发生过 2 次被盗,别墅的主人有一条狗,狗平均每周晚上叫 3 次,在盗贼入侵时狗叫的概率被估计为 0.9,问题是:在狗叫的时候发生入侵的概率是多少?
我们假设 A 事件为狗在晚上叫,B 为盗贼入侵,则 P(A) = 3 / 7,P(B)=2/(20·365)=2/7300,P(A | B) = 0.9,按照公式很容易得出结果:P(B|A)=0.9*(2/7300)/(3/7)=0.00058
容器里的球
另一个例子,现分别有 A,B 两个容器,在容器 A 里分别有 7 个红球和 3 个白球,在容器 B 里有 1 个红球和 9 个白球,现已知从这两个容器里任意抽出了一个球,且是红球,问这个红球是来自容器 A 的概率是多少?
假设已经抽出红球为事件 B,从容器 A 里抽出球为事件 A,则有:P(B) = 8 / 20,P(A) = 1 / 2,P(B | A) = 7 / 10,按照公式,则有:P(A|B)=(7 / 10)*(1 / 2)/(8/20)=0.875
贝叶斯公式为利用搜集到的信息对原有判断进行修正提供了有效手段。在采样之前,经济主体对各种假设有一个判断(先验概率),关于先验概率的分布,通常可根据经济主体的经验判断确定(当无任何信息时,一般假设各先验概率相同),较复杂精确的可利用包括最大熵技术或边际分布密度以及相互信息原理等方法来确定先验概率分布。
贝叶斯定理的推广
对于变量有二个以上的情况,贝式定理亦成立。例如:
P(A|B,C)=P(B|A)*P(A)*P(C|A,B)/(P(B)*P(C|B))
这个式子可以由套用多次二个变量的贝式定理及条件机率的定义导出:
贝叶斯理论及应用
| 数学领域 | ▪ 贝叶斯分类算法 (应用:统计分析、测绘学) ▪ 贝叶斯公式 (应用:概率空间) ▪ 贝叶斯区间估计 (应用:数学中的区间估计) ▪ 贝叶斯序贯决策函数 (应用:统计决策论) |
▪ 贝叶斯风险 (应用:统计决策论) ▪ 贝叶斯估计 (应用:参数估计) ▪ 贝叶斯统计 (应用:统计决策论) ▪ 经验贝叶斯方法 (应用:统计决策论) |
| 工程领域 | ▪ 贝叶斯定理 (应用:人工智能、心理学、遗传学) ▪ 贝叶斯分析 (应用:计算机科学) ▪ 贝叶斯逻辑 (应用:人工智能) ▪ 贝叶斯网络 (应用:人工智能) |
▪ 贝叶斯分类器 (应用:模式识别、人工智能) ▪ 贝叶斯决策 (应用:人工智能) ▪ 贝叶斯推理 (应用:数量地理学、人工智能) ▪ 贝叶斯学习 (应用:模式识别) |
| 其他领域 | ▪ 贝叶斯主义 (应用:自然辩证法) | ▪ 有信息的贝叶斯决策方法 (应用:生态系统生态学) |
【例子】水果糖问题
为了加深对贝叶斯推断的理解,我们看两个例子。

第一个例子。两个一模一样的碗,一号碗有30颗水果糖和10颗巧克力糖,二号碗有水果糖和巧克力糖各20颗。现在随机选择一个碗,从中摸出一颗糖,发现是水果糖。请问这颗水果糖来自一号碗的概率有多大?
我们假定,H1表示一号碗,H2表示二号碗。由于这两个碗是一样的,所以P(H1)=P(H2),也就是说,在取出水果糖之前,这两个碗被选中的概率相同。因此,P(H1)=0.5,我们把这个概率就叫做"先验概率",即没有做实验之前,来自一号碗的概率是0.5。
再假定,E表示水果糖,所以问题就变成了在已知E的情况下,来自一号碗的概率有多大,即求P(H1|E)。我们把这个概率叫做"后验概率",即在E事件发生之后,对P(H1)的修正。
根据条件概率公式,得到
已知,P(H1)等于0.5,P(E|H1)为一号碗中取出水果糖的概率,等于0.75,那么求出P(E)就可以得到答案。根据全概率公式,
所以,
将数字代入原方程,得到
这表明,来自一号碗的概率是0.6。也就是说,取出水果糖之后,H1事件的可能性得到了增强。
贝叶斯过滤器
垃圾邮件是一种令人头痛的顽症,困扰着所有的互联网用户。
正确识别垃圾邮件的技术难度非常大。传统的垃圾邮件过滤方法,主要有"关键词法"和"校验码法"等。前者的过滤依据是特定的词语;后者则是计算邮件文本的校验码,再与已知的垃圾邮件进行对比。它们的识别效果都不理想,而且很容易规避。
2002年,Paul Graham提出使用"贝叶斯推断"过滤垃圾邮件。他说,这样做的效果,好得不可思议。1000封垃圾邮件可以过滤掉995封,且没有一个误判。
另外,这种过滤器还具有自我学习的功能,会根据新收到的邮件,不断调整。收到的垃圾邮件越多,它的准确率就越高。
贝叶斯过滤器是一种统计学过滤器,建立在已有的统计结果之上。所以,我们必须预先提供两组已经识别好的邮件,一组是正常邮件,另一组是垃圾邮件。
我们用这两组邮件,对过滤器进行"训练"。这两组邮件的规模越大,训练效果就越好。Paul Graham使用的邮件规模,是正常邮件和垃圾邮件各4000封。
"训练"过程很简单。首先,解析所有邮件,提取每一个词。然后,计算每个词语在正常邮件和垃圾邮件中的出现频率。比如,我们假定"sex"这个词,在4000封垃圾邮件中,有200封包含这个词,那么它的出现频率就是5%;而在4000封正常邮件中,只有2封包含这个词,那么出现频率就是0.05%。(【注释】如果某个词只出现在垃圾邮件中,Paul Graham就假定,它在正常邮件的出现频率是1%,反之亦然。这样做是为了避免概率为0。随着邮件数量的增加,计算结果会自动调整。)
有了这个初步的统计结果,过滤器就可以投入使用了。
现在,我们收到了一封新邮件。在未经统计分析之前,我们假定它是垃圾邮件的概率为50%。(【注释】有研究表明,用户收到的电子邮件中,80%是垃圾邮件。但是,这里仍然假定垃圾邮件的"先验概率"为50%。)
我们用S表示垃圾邮件(spam),H表示正常邮件(healthy)。因此,P(S)和P(H)的先验概率,都是50%。
然后,对这封邮件进行解析,发现其中包含了sex这个词,请问这封邮件属于垃圾邮件的概率有多高?
我们用W表示"sex"这个词,那么问题就变成了如何计算P(S|W)的值,即在某个词语(W)已经存在的条件下,垃圾邮件(S)的概率有多大。
根据条件概率公式,马上可以写出
公式中,P(W|S)和P(W|H)的含义是,这个词语在垃圾邮件和正常邮件中,分别出现的概率。这两个值可以从历史资料库中得到,对sex这个词来说,上文假定它们分别等于5%和0.05%。另外,P(S)和P(H)的值,前面说过都等于50%。所以,马上可以计算P(S|W)的值:
因此,这封新邮件是垃圾邮件的概率等于99%。这说明,sex这个词的推断能力很强,将50%的"先验概率"一下子提高到了99%的"后验概率"。
做完上面一步,请问我们能否得出结论,这封新邮件就是垃圾邮件?
回答是不能。因为一封邮件包含很多词语,一些词语(比如sex)说这是垃圾邮件,另一些说这不是。你怎么知道以哪个词为准?
Paul Graham的做法是,选出这封信中P(S|W)最高的15个词,计算它们的联合概率。(【注释】如果有的词是第一次出现,无法计算P(S|W),Paul Graham就假定这个值等于0.4。因为垃圾邮件用的往往都是某些固定的词语,所以如果你从来没见过某个词,它多半是一个正常的词。)
所谓联合概率,就是指在多个事件发生的情况下,另一个事件发生概率有多大。比如,已知W1和W2是两个不同的词语,它们都出现在某封电子邮件之中,那么这封邮件是垃圾邮件的概率,就是联合概率。
在已知W1和W2的情况下,无非就是两种结果:垃圾邮件(事件E1)或正常邮件(事件E2)。

其中,W1、W2和垃圾邮件的概率分别如下:

如果假定所有事件都是独立事件(【注释】严格地说,这个假定不成立,但是这里可以忽略),那么就可以计算P(E1)和P(E2):
又由于在W1和W2已经发生的情况下,垃圾邮件的概率等于下面的式子:
即
将P(S)等于0.5代入,得到
将P(S|W1)记为P1,P(S|W2)记为P2,公式就变成
这就是联合概率的计算公式。
将上面的公式扩展到15个词的情况,就得到了最终的概率计算公式:
一封邮件是不是垃圾邮件,就用这个式子进行计算。这时我们还需要一个用于比较的门槛值。Paul Graham的门槛值是0.9,概率大于0.9,表示15个词联合认定,这封邮件有90%以上的可能属于垃圾邮件;概率小于0.9,就表示是正常邮件。
有了这个公式以后,一封正常的信件即使出现sex这个词,也不会被认定为垃圾邮件了。
转自:https://www.cnblogs.com/skyme/p/3564391.html