所谓二分图,是可以分为两个点集的图;
所谓二分图最大匹配,是两个点集之间,每两个不同点集的点连接,每个点只能连一个点,最大的连接数就是最大匹配。
如何解最大匹配,需要用到匈牙利算法。
另:本文写了很多细节,有的地方比较啰嗦,请大佬放过
匈牙利算法是一个递归的过程,它的特点,我觉得可以归为一个字:“让”。
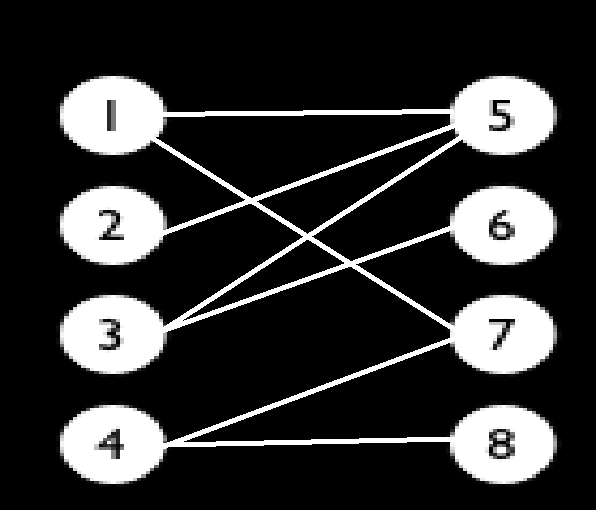
例如这张图,按照匈牙利算法的思路就是:
1.1与5匹配,5没有被标记,将5标记,记录1与5匹配
2.清空标记
3.2与5匹配,5没有被标记,将5标记,发现5已经与1匹配,在[此处]重新递归1:
①1与5匹配,发现5已经被标记,跳出
②1与7匹配,发现7没有被标记,将7标记,记录1与7匹配,返回成功
4.回到2与5匹配的[此处],发现返回成功,则直接记录2与5匹配
5.清空标记
6.3与5匹配,5没有被标记,将5标记,发现5已经与2匹配,在[此处]重新递归2:
①2与5匹配,发现5已经被标记,跳出
②2没有其他连接的边了,返回失败
7.回到3与5匹配的[此处],发现返回失败,继续查找与3连接的边
8.3与6匹配,6没有被标记,将6标记,记录3与6匹配
9.清空标记
9.4与7匹配,7没有被标记,将7标记,发现7已经与1匹配,在[此处]重新递归1:
①1与5匹配,5没有被标记,将5标记,发现5已经与2匹配,在[此处A]重新递归2:
①2与5匹配,发现5已经被标记,跳出
②2没有连接的边了,返回失败
②回到1与5匹配的[此处A],发现返回失败,继续查找1连接的边
③1与7匹配,发现7已经被标记,跳出
④1没有可以连接的边了,返回失败
10.回到4与7匹配的[此处],发现返回失败,继续查找与4连接的边
11.4与8匹配,8没有被标记,将8标记,记录4与8匹配
12.清空标记
13.左边的点集枚举完毕,从记录中得到:1与7匹配,2与5匹配,3与6匹配,4与8匹配
这就是匈牙利算法(这就是人脑编译器吗)
用人话来说,就是
1:诶,你看我找到我连接的第一个,是一个没人占据的点啊,我和5匹配吧
2:诶,你看我找到我连接的第一个就是5,竟然被1占据了!可恶,1你再去找找有没有别的边去匹配!
1:我要匹配5!
2:这是我要匹配的!
1:好吧,我看看,我连接的第二个,是一个没人占据的边啊,我和7匹配吧
2:好棒啊,那我就和5匹配了
3:我连接的第一个边是5,居然被2占据了,2你去看看有没有别的边匹配啊
2:好,我第一个连接的点就是5,我要连接5!
3:我要和5匹配!泥奏凯!
2:好吧,那我连接的第二个点。。没有第二个点,我只有匹配5了!!!
3:我去,这么不凑巧,那好吧,我只好找找我连接的第二个点了,只有6了,6还没有被人占据,我捷足先登,嘿嘿嘿
4:我第一个连接的点是7,竟然被1占据了, 可恶,1给我等着,你去看看有没有别的边
1:我第一个连接的点是5,但是被2占据了,如果想让我给你挪腾地方的话,我只好先让2换个地方
2:那么我第一个连接的点是5,1你要用的话我就不可以匹配它。我没有第二个连接的点,因此1对不起,我不能给你挪腾地方
1:那好吧,那么我第二个连接的点是7——
4:我要这个点啊!本来我的目的就是让你挪腾地方离开7啊
1:那我没地可以挪腾了,爱能莫助啊~~~
4:那好吧,看看我连接的第二个点8,看来这个点没有被人占据,那么我就和它匹配
至此,所有的点都找到归属了。
(这tm不就是翻译过来吗,哪有正常人这么说话)
咳咳咳,anyway,匈牙利算法就是这样一个神奇的算法。
总结一下,从某种意义上来说,匈牙利算法算是一个动态规划。
为了读者理解方便,这里规定:我们枚举的点集用小写字母表示,另一个点集用大写字母表示。
因为由它的递归结构决定,只要一个点当前要匹配的点(设它为A)与另外的点(设它为B)要与同一个点(设它为c)匹配(为什么它们都要与c匹配的原因就是A是按照顺序依次匹配的,每一个A连接的点都要被依次尝试,由于匈牙利算法的内容决定的它的性质,因此无论顺序如何最后得到的都是最优的局面),那么A可以在B找到除了c以外的其它匹配的前提下达成对于A的最优局面,即A匹配c,B匹配另外的点。这样原来的匹配数不变,又增加了一条匹配。
如果B通过递归无法找到其它匹配,那么如果舍弃B这个匹配换上A的匹配,并不会增加匹配数。因此,这个策略是最优的。
但是这样说还不够,为什么就能保证A以前的匹配都是最优的呢?这样就必须说说B的递归匹配过程。
A要匹配c,那么让B与除了C以外的点匹配。如果B直接找到了未匹配的点(除了c,下同),那么直接匹配。如果B没有直接找到未匹配的点,那么B连接的边一定都是已经匹配其它点的。那么B就会尝试改变B要匹配的点(设它为d)的匹配的点(设它为E)的匹配,与A让B更换匹配一样,让E更换匹配为除了d以外的匹配点,这样B就可以得到d这个点的匹配了。然后,E重复B的过程......如此这般,如果一直找不到可以直接匹配的点的话,可以回溯到第一次匹配。这样,所有的匹配都会更换为:「在不改变原有匹配数的情况下,对A最优的局面,也就是对A匹配c最优的局面」,因此,每次匹配,总是会造成对当前局面的最优的匹配,如果局部不是最优,那么一旦涉及到需要这块局部最优的时候,这块将会同样被回溯到然后更改为最优。(这里的最优都是指的对当前局面的最优)。
当然,相信有聪明的同学已经想到,如果这样匹配的话,万一整个二分图不是联通图怎么办。很简单,如果按照上面代码的写法,每个连通块相当于一个二分图,每个二分图的匹配按照上面的写法总是最优的,最后的统计最大匹配只需要把每个连通块的最大匹配相加就可以了。
太长不看版:牵一发,动全身。每一次的尝试匹配的操作都会造成对当前整个图的匹配的调整,无论之前是怎样的图,最后都会被调整到对当前匹配最有利的图。
至于如何证明它的正确性,必须要这样一个东西来帮助我们:
增广路,它的性质是:(匹配点/边用1表示,非匹配点/边用0表示,N表示点/边的个数)
第一条边是非匹配边,然后到匹配边,然后到非匹配边......最后的边一定是非匹配边,并且边的个数一定是奇数。(01010101...0,N mod 2 ≠ 0)
那么匈牙利算法的实质,或者说另一种形式,就是不断寻找增广路来扩大匹配。
(我看的书上并没有增广路和匈牙利算法的关系,那么在这里详细说明是如何寻找增广路的)
在上面的描述中,我们知道,匈牙利算法的基本结构是枚举一个点集,通过上述方式“让”出最大匹配。
但是在“让”的过程中,我们发现,之前的操作,实际上都符合寻找增广路的方法。
例如,我们在匹配2的过程中(请回顾之前的模拟匈牙利算法的那段),
增广路的第一个点是2,接着经过那些操作,与2匹配的点是5,那么第二个点就是5。而之前与5匹配的点是1,1现在又7匹配。
则为:2->5->1->7
如果我们把更换匹配之前的匹配边称作匹配边,会发现:
2->5在更换匹配之前没有匹配,为非匹配边。
5->1在更换匹配之前是匹配的,为匹配边。
1->7在更换之前是没有匹配的,为非匹配边。
正好符合我们的增广路定义!其中,1->7就是我们增加的边。
为什么会这样?
让我们再来解说一次,用红色和蓝色来区分增广路和“让”的方法:
为了说明方便,这里假设最后匹配到了可以直接匹配的点,也就是说增广路发现成功
首先,增广路的第一个边必定是非匹配边。
我们枚举点集的时候必定没有枚举过当前枚举的点(设它为P),那么P之前没有与任何边匹配,所以与P相连的边是非匹配边,设与P相连的点为i。
如果i原来不是匹配点,那么这条增广路已经结束,不存在第二条边,最后一条边是非匹配边。
然后,增广路的第二条边必定是匹配边,最后一条边必定是非匹配边。
同上,如果P连接的i原来不是匹配点,则增广路结束,第二条边不存在,而第一条边也是最后一条边,也符合定义。
如果i原来是匹配点,设X为i原来匹配的点,因为P为非匹配点,则X≠P,则X必定是这条增广路的第三个点,则这条边,也就是第二条边,是匹配边。
接着,增广路的第三条边必定是非匹配边
这儿分两种情况,第一是X更换到的点(设它为y)是非匹配点,可以直接匹配,那么因为y是非匹配点,则X->y是非匹配边,符合定义。
第二是y已经匹配了,由于X原来是匹配点,而一个点只能匹配一个点,X已经与i匹配,则y原来必定与X不匹配,则这条边(X->y)原来必定不是匹配边。符合定义。
...剩下同理
因此,只要最后找到了未匹配点,都算找到了增广路。
---------------------------
模板题HDU - 1083

#include <cstdio> #include <cstring> const int MaxN = 500; int ask[MaxN]; int vis[MaxN][MaxN]; int matched[MaxN]; int n,m;//n:课程人数,m:学生人数 int ans; bool find(int from) { for(int i = 1; i <= m; i++){ if(vis[from][i]){ if(!ask[i]){ ask[i] = 1; if(!matched[i] || find (matched[i])){ matched[i] = from; return 1; } } } } return 0; } void match(){ int count = 0; memset(matched,0,sizeof(matched)); for(int i = 1; i <= n; i++){ memset(ask,0,sizeof(ask)); if(find(i)) count ++; } ans = count ; } int main() { int data_p; scanf("%d",&data_p); while(data_p--){ scanf("%d%d",&n,&m); for(int i = 1; i <= m; i++){ int num = 0; scanf("%d",&num); for(int j = 1; j <= num; j++){ int tmp; scanf("%d",&tmp); vis[i][tmp] = 1; } } match(); if(ans == n){ printf("YES "); } else{ printf("NO "); } memset(vis,0,sizeof(vis)); ans = 0; } return 0; }
先在match函数中枚举每个左集的点,每个左集的点调用Find函数。
Find中,枚举右集的点,找匹配,将匹配到的点标记,如果这个标记了的点没有被匹配或者递归上去能找到其他点匹配,那么就把当前点匹配。
最后,记录matched数组中的个数,即为最大匹配。
---------------------------
HDU - 3729

#include <cstdio> #include <cstring> #include <cmath> #include <algorithm> const int MaxN = 100010; struct EDGE{ int to,nxt; }edge[MaxN]; int head[100];//[]点最后一个连接的边 int e_num;//边的数量 void add(int u,int v){ edge[++e_num].to = v; edge[e_num].nxt = head[u]; head[u] = e_num; } int n,ans; bool ask[MaxN]; int matched[MaxN]; int q[MaxN]; bool Find(int u){ for(int i = head[u]; i ; i = edge[i].nxt){ //if(edge[u][i]){ if(!ask[edge[i].to]){ ask[edge[i].to] = 1; //printf("new : %d->%d ",u,edge[i].to); if(!matched[edge[i].to] || Find(matched[edge[i].to])){ matched[edge[i].to] = u; //printf("best match! %d|%d ",u,i); //printf("matched[%d] = %d ",i,matched[i]); return true; } } //} } return false; } void match(){ memset(matched,0,sizeof(matched)); int count = 0; for(int i = n; i >= 1; i --){ memset(ask,0,sizeof(ask)); if(Find(i)) count ++; } ans = count; } int main() { int data_n; scanf("%d",&data_n); while(data_n--){ memset(edge,0,sizeof(edge)); memset(head,0,sizeof(head)); e_num = 0; scanf("%d",&n); for(int i = 1; i <= n; i++){ int x1,x2; scanf("%d%d",&x1,&x2); for(int j = x1; j <= x2; j++){ //edge[i][j] = 1; add(i,j); } } /*debug for(int i = 1; i <= n; i++){ for(int j = head[i] ; j ; j = edge[j].nxt){ printf("%d - > %d ",i,edge[j].to); } } //debug*/ match(); printf("%d ",ans); int cnt = 0; memset(q,0,sizeof(q)); for(int j = 1; j <= 100000; j++){ if(matched[j]){ q[++cnt] = matched[j]; } } std::sort(q+1,q+cnt+1); for(int j = 1; j <= cnt; j++){ printf("%d",q[j]); if(j != cnt) printf(" "); //printf("|end|"); } //if(data_n != 0) printf(" "); } return 0; } /* 2 4 5004 5005 5005 5006 5004 5006 5004 5006 7 4 5 2 3 1 2 2 2 4 4 2 3 3 4 */
几乎是模板题,只不过数据有10万,并且需要最大字典序输出,只需要把之前的邻接矩阵改成邻接表即可提高速度,
只要把左集倒序枚举即可得到最大字典序答案。
窃以为理解透彻了,将思路全部放上来,可能有些啰嗦。
写到后面脑子很乱,不知道该如何表达,不对地方还请指正
