对偶图是一种神奇的东西!
对于一个平面图(G=(V,E))(也就是能画在平面上,且边的交点都在顶点处的图),则它的对偶图(G^*)的定义如下:
1.(G^*)的每一个顶点对应(G)中的每一个面
2.对于(G)中的边(e),若它的两侧为两个不同的平面(f_1^*)和(f_2^*),则在(G^*)中有一个对应的边((f_1^*,f_2^*)),若为同一个平面(f_1^*),则对应一个自环((f_1^*,f_2^*))
比较抽象,可以结合下面的图理解(绿边为对偶图的边):
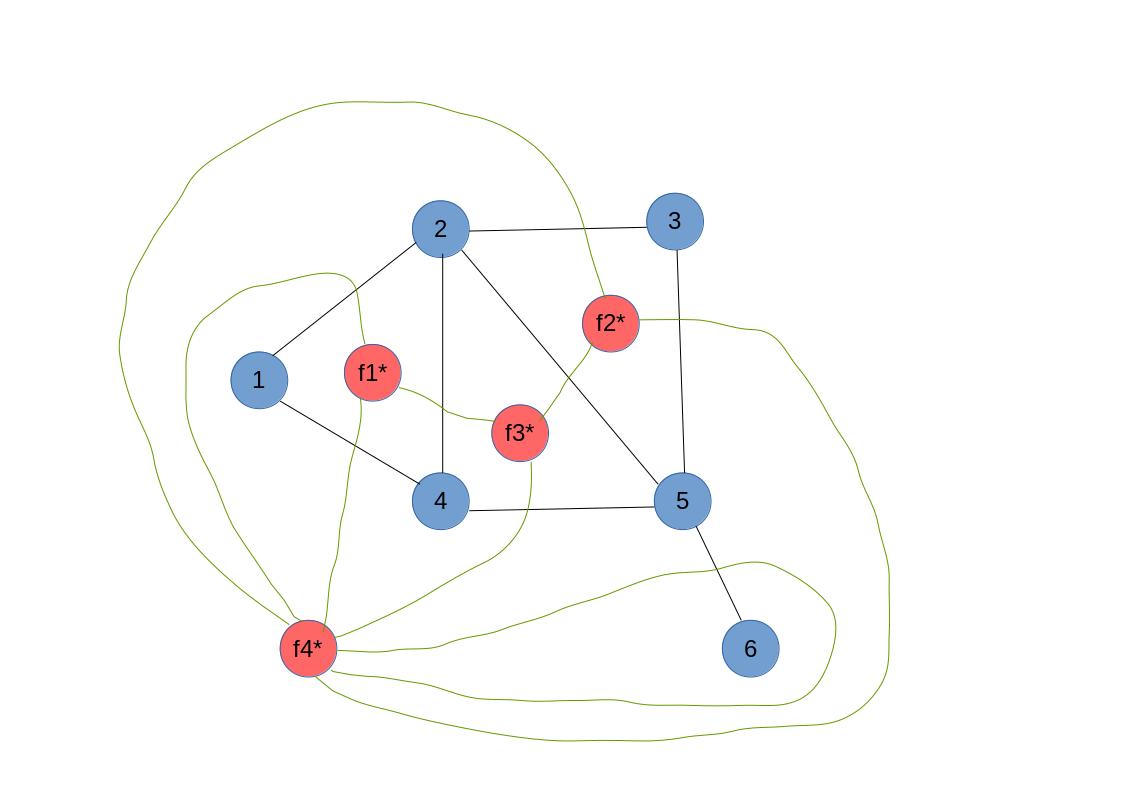
注意,((5,6))使得(G^*)中多了一个((f_4^*,f_4^*))的自环
对偶图的好处是什么呢?有如下两条:
1.对偶图(G^*)中的一个环对应(G)中的一个割
2.最大流和最小割可以在对偶图中转化为最短路
(两条性质貌似想一想就很显然啦QwQ)
第二条性质很重要,可以极大地优化时间复杂度。但怎么把最大流(或最小割)转化到对偶图中来呢?
比如对于上图,假设源点(S),汇点(T)分别为(1),(6)。首先我们先在(G)中在(1),(6)间连一条虚边:
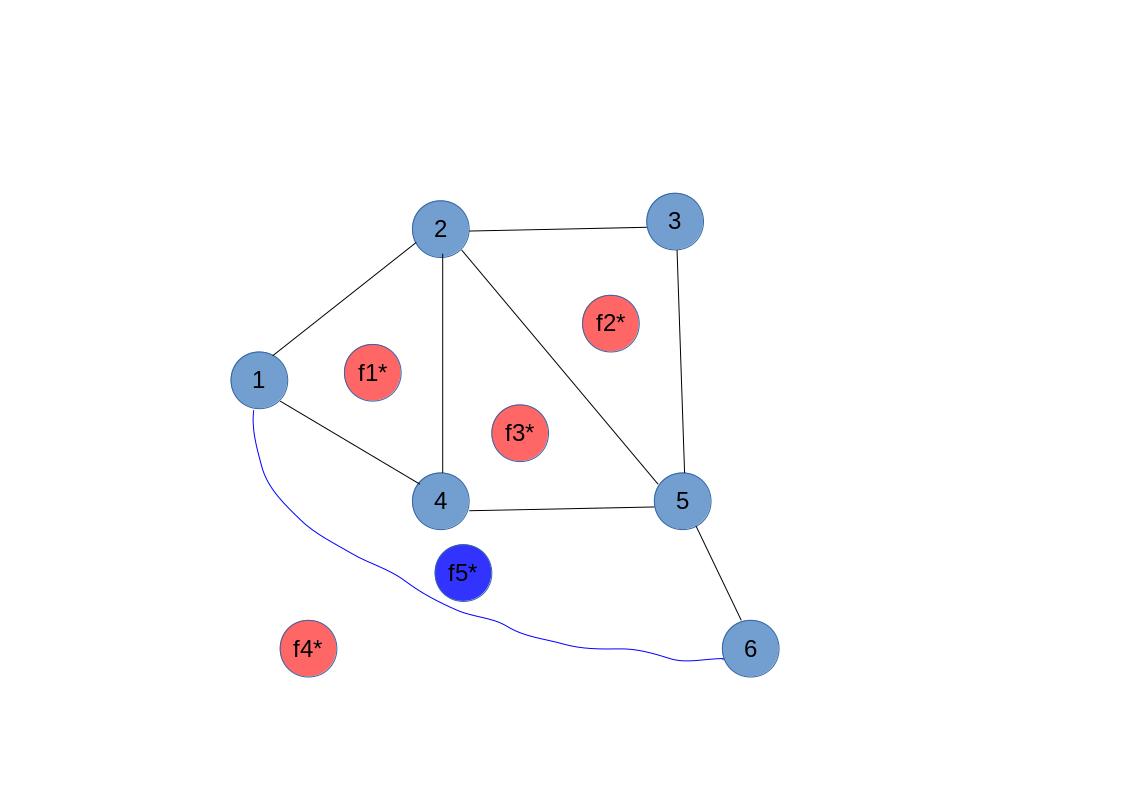
这样就多出了一个平面(f_5^*)。然后让(f_5^*)对应(S),(f_4^*)(无界面)对应(T),再建一个对偶图就行了(虚边不用管,即蓝色的那条):
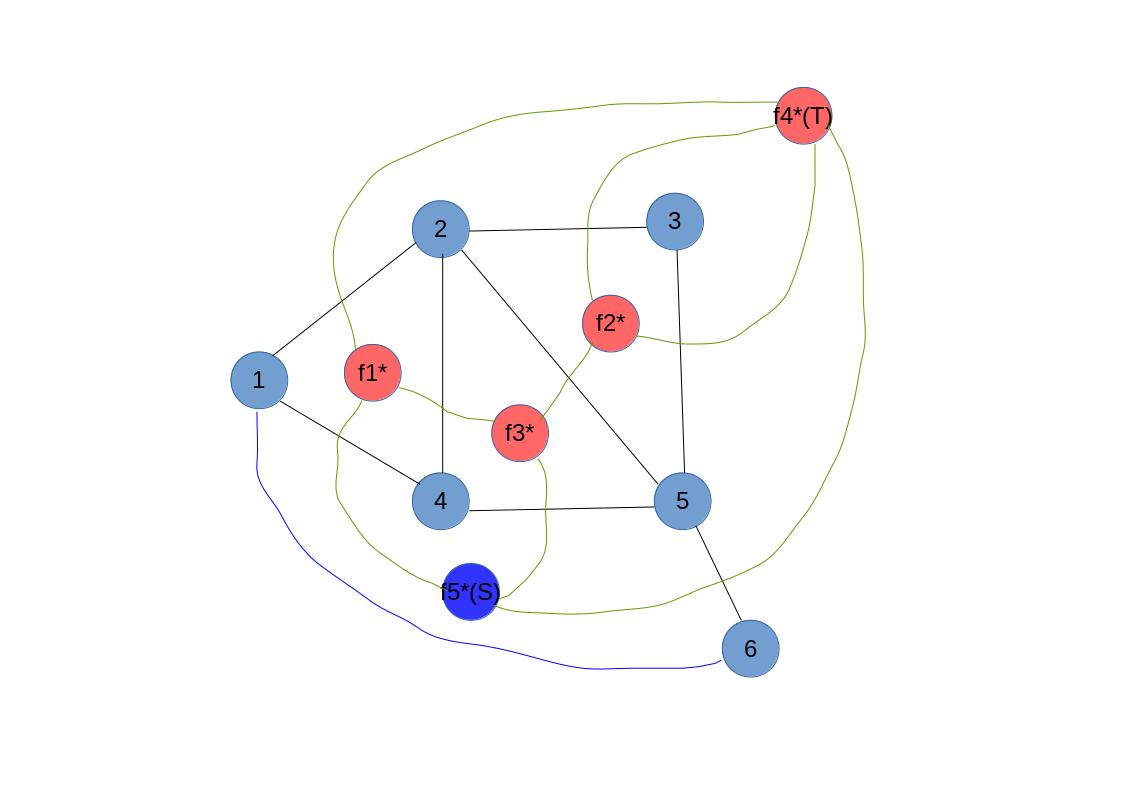
最大流或最小割就变成(S)到(T)的最短路啦!就可以上(dij)了