HDU 6069 Counting Divisors (素数+筛法)

题意：给定 l，r，k，让你求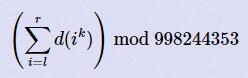，其中 l <= r <= 1e12, r-l <= 1e6, k <= 1e7。

析：首先这个题肯定不能暴力，但是给定的区间较小，可以考虑筛选，n = p1^c1*p2^c2*....*pn^cn，那么 d(n) = (c1+1) * (c2+1) * ...*(cn+1)。

d(n^k) =  (kc1+1) * (kc2+1) * ...*(kcn+1)，这样的话，我们只要求出每个数的素因子的个数就好，直接算还是不行，只能先把1-sqrt(n)之间的素数先算出来，这个是可以实现的，然后再考虑枚举素数，然后计算在 l - r 这个区间内的数进行筛选，也就是说从第一个能整除prime[i]的数开始，假设是x，先把prime[i]除尽，然后再把 x 加上prime[i]，再除尽，依次。。。这样的话，复杂度会小很多。注意mod的不是1e9+7

代码如下：

#pragma comment(linker, "/STACK:1024000000,1024000000")
#include <cstdio>
#include <string>
#include <cstdlib>
#include <cmath>
#include <iostream>
#include <cstring>
#include <set>
#include <queue>
#include <algorithm>
#include <vector>
#include <map>
#include <cctype>
#include <cmath>
#include <stack>
#include <sstream>
#include <list>
#define debug() puts("++++");
#define gcd(a, b) __gcd(a, b)
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
#define freopenr freopen("in.txt", "r", stdin)
#define freopenw freopen("out.txt", "w", stdout)
using namespace std;

typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int, int> P;
const int INF = 0x3f3f3f3f;
const double inf = 1e20;
const double PI = acos(-1.0);
const double eps = 1e-8;
const int maxn = 1e6 + 10;
const LL mod = 998244353;
const int dr[] = {-1, 0, 1, 0};
const int dc[] = {0, 1, 0, -1};
const char *de[] = {"0000", "0001", "0010", "0011", "0100", "0101", "0110", "0111", "1000", "1001", "1010", "1011", "1100", "1101", "1110", "1111"};
int n, m;
const int mon[] = {0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
const int monn[] = {0, 31, 29, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
inline bool is_in(int r, int c) {
    return r > 0 && r <= n && c > 0 && c <= m;
}
vector<int> prime;
bool vis[maxn];

void init(){
  for(int i = 2; i < maxn; ++i)  if(!vis[i]){
    prime.push_back(i);
    if(i > 1000)  continue;
    for(int j = i*i; j < maxn; j += i)  vis[j] = 1;
  }
}

LL sum[maxn], a[maxn];

int main(){
  init();
  int T;  cin >> T;
  while(T--){
    LL k, n, m;
    scanf("%I64d %I64d %I64d", &m, &n, &k);
    for(int i = 0; i <= n-m; ++i){
      sum[i] = 1LL;
      a[i] = i + m;
    }

    for(int i = 0; i < prime.size(); ++i){
      LL st = (LL)(m/prime[i] + (m%prime[i] != 0)) * prime[i];
      for(LL j = st; j <= n; j += prime[i]){
        int res = 0;
        while(a[j-m] % prime[i] == 0){
          ++res;  a[j-m] /= prime[i];
        }
        sum[j-m] = ((k * res % mod + 1LL) * sum[j-m]) % mod;
      }
    }

    LL ans = 0;
    for(int i = 0; i <= n - m; ++i){
      if(a[i] > 1LL)  sum[i] = sum[i] * (k + 1) % mod;
      ans = (ans + sum[i]) % mod;
    }
    printf("%I64d
", ans);
  }
  return 0;
}