<组合数学>排列组合(1)/格路模型，范德蒙德恒等式

1.排列(permutation)：

　　从n个不同的元素中，取出r个不重复的元素，按次序排列，称为从n个中取r个的无重排列。

　　排列的个数用P(n,r)表示或P^r_n     n>=r       //高中的时候教材教我们A^r_n ，跟这里的一样。

　　P(n,r) = n!/r!

　　排列的基本问题是“n个不同球放r个不同盒”问题。

2.组合(conmutation)：

　　从n个不同的元素中，取出r个不重复的元素组成一个子集而不考虑其元素的顺序，称为从n个中取r个的无重组合。

　　组合的个数用C(n,r)表示或C^r_n     n>=r

　　C(n,r)=n! / [r!*(n-r)!]

　　组合的基本问题是“n个不同球放r个相同盒”问题。

　　两个性质：

　　　　|—— C(n,r) = C(n,n-r)           //C(8,3)=C(8,5)

　　　　|—— C(n,l)*C(l,r) = C(n,r)*C(n-r,l-r) //C(9,5)*C(5,2)=C(9,2)*C(7,3)

3.格路模型与组合恒等式：

组合数学有一个研究方向就是研究组合恒等式。

格路模型

我们把从（0，0）到（m，n）的路径用一个形如“xxyxyyxy...xyy”的字符串表示。

则字符串长度为m+n，有m个‘x’，n个‘y’。

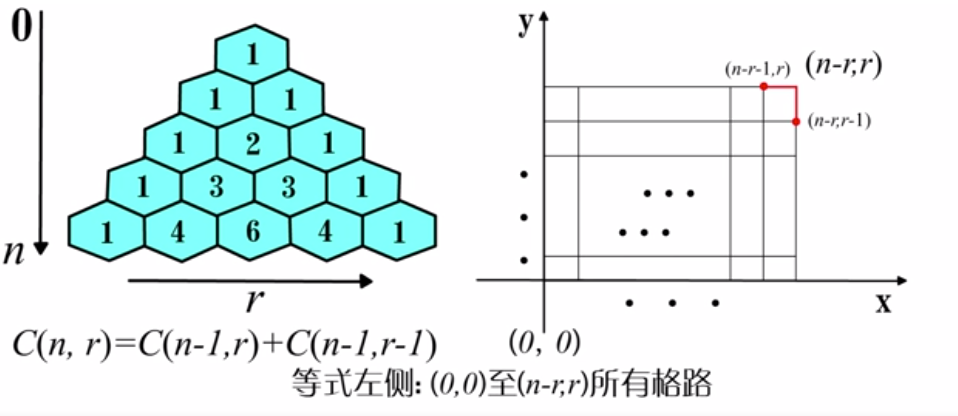
杨辉三角用于格路模型

在杨辉三角中，第n行对应着(a+b)ⁿ的系数，第n行第r列的数值是C(n,r)

 

范德蒙德恒等式