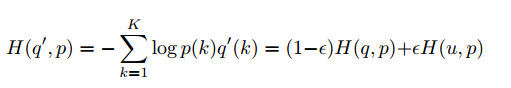一. bags of specials
1. swish激活函数
f(x) = x • sigmoid(x)

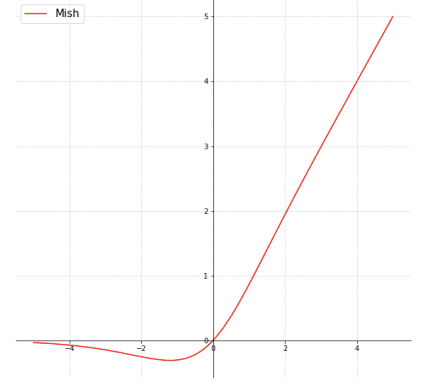
2. Mish 激活函数
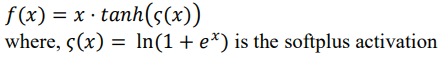
3. spatial pyramid pooling(SPP)
citehttps://arxiv.org/abs/1406.4729
传统的卷积神经网络,对输入图像的大小有严格要求,例如LeNet5只能为224x224,这要求我们在使用网络前需要对图像进行一些预处理操作.为了解决这个麻烦,何恺明发明了SPP这个局部结构,把SPP放在卷积层和全连接层之间,从而很好地解决了这个问题.
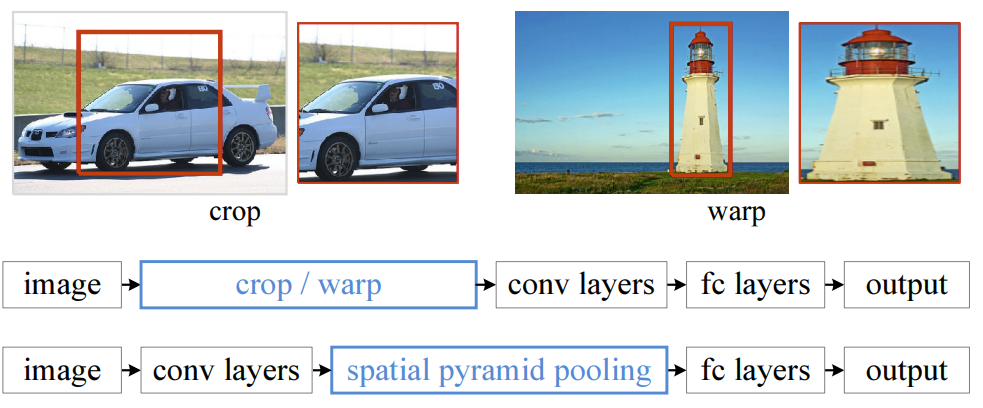
下面是一个例子:
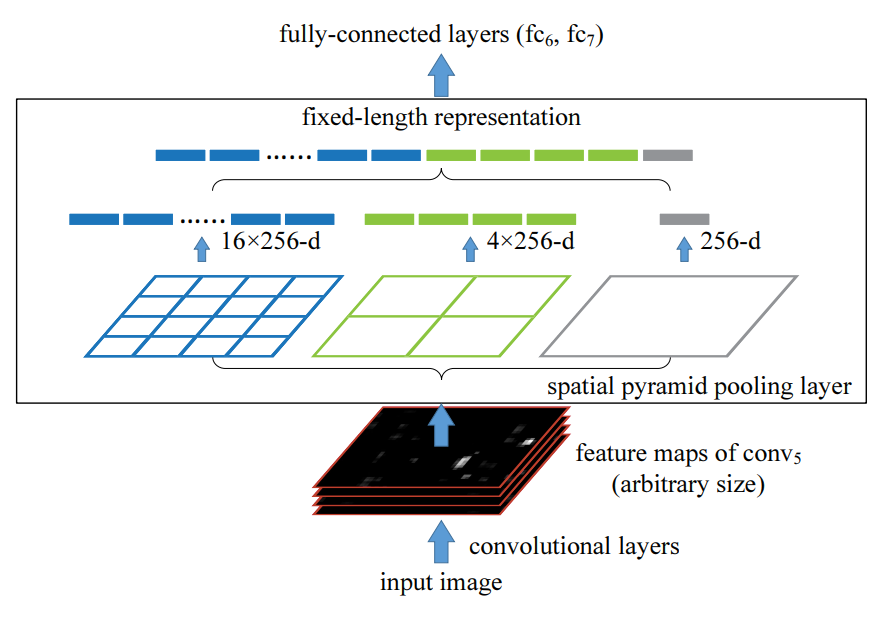
图像经过卷积层,来到全连接层前面, 在input image size不确定的情况下(可能224x224,可能256x448),它经过层层卷积处理后的输出,即一组feature map的数量是固定的,只是feature map size 不确定.然而接下来的全连接层的输入量是固定的(4096), 我们对这些feature maps进行以下处理再输入到全连接层里:
假设有256张feature map
对256张feature map分别进行如图所示的三种max-pooling,控制三种max-pooling的输出严格为4x4 size, 2x2 size, 1x1 size, 将这些输出cancatenate到一起作为全连接层的输入.如上操作即为SPP处理.

4. 特征融合Feature Pyramid Network (FPN)
citehttps://arxiv.org/abs/1612.03144
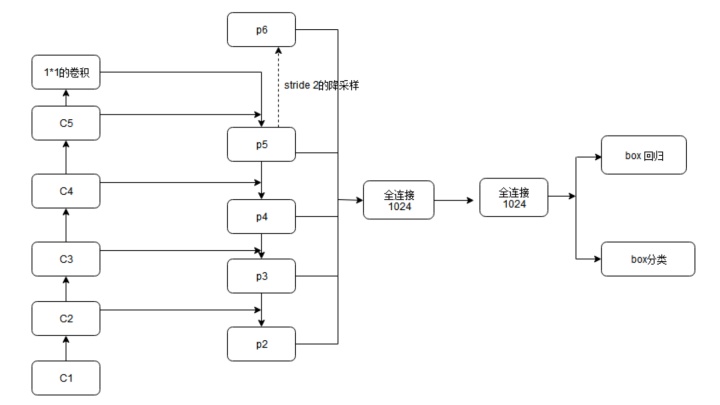
5. Squeeze-and-Excitation(SE)
citehttps://arxiv.org/abs/1709.01507
一种channel-wise的注意力机制
下图从U的输出到X的输出这段即为SE

直接说,
Squeeze: 先对U做一个global average pooling
Excitation: 输出的1x1xC数据做两级全连接,最后sigmoid限制到[0,1]的范围.
Scale: 然后把这个值对应着乘到U的C个通道上,作为下一级的输入.
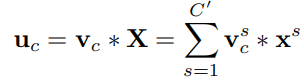
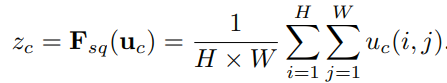
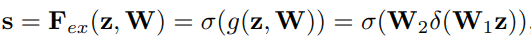
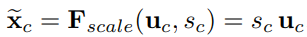
两个例子:

6. Spatial Attention Module
一种point-wise的注意力机制
对feature maps, 分别从通道维度进行求平均值和求最大, 合并得到一个通道数为2的卷积层,然后通过一个卷积,得到一个通道数为1的spatial attention.
直观图示:

准确代码实现:
#cite https://zhuanlan.zhihu.com/p/102035273 class SpatialAttention(nn.Module): def __init__(self, kernel_size=7): super(SpatialAttention, self).__init__() assert kernel_size in (3,7), "kernel size must be 3 or 7" padding = 3 if kernel_size == 7 else 1 self.conv = nn.Conv2d(2,1,kernel_size, padding=padding, bias=False) self.sigmoid = nn.Sigmoid() def forward(self, x): avgout = torch.mean(x, dim=1, keepdim=True) maxout, _ = torch.max(x, dim=1, keepdim=True) x = torch.cat([avgout, maxout], dim=1) x = self.conv(x) return self.sigmoid(x)
yolov4中作了微调,改为了

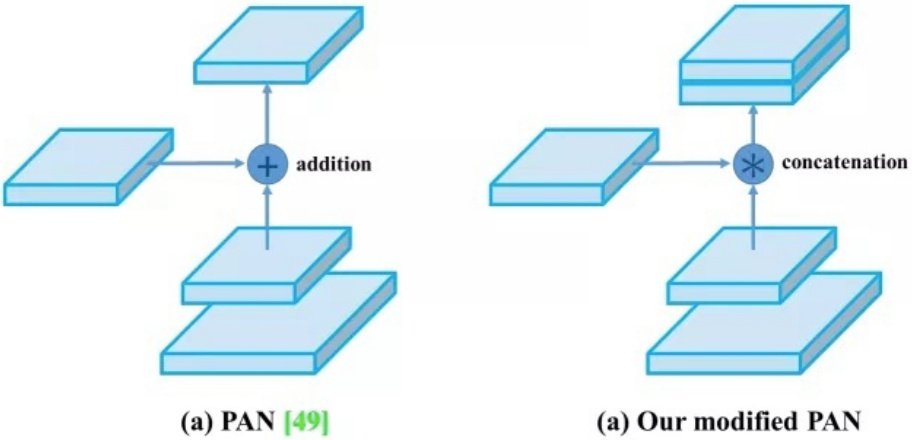
9. PAN
yolov4中用到的微调的PAN
二. bags of freebies
1. dropblock正则化

DropBlock是dropout的一种结构化形式. 在DropBlock中,特征在一个block中, 例如一个feature map中的连续区域会一起被drop掉.当DropBlock抛弃掉相关区域的特征时,为了拟合数据网络就不得不往别处看以寻找新的证据.

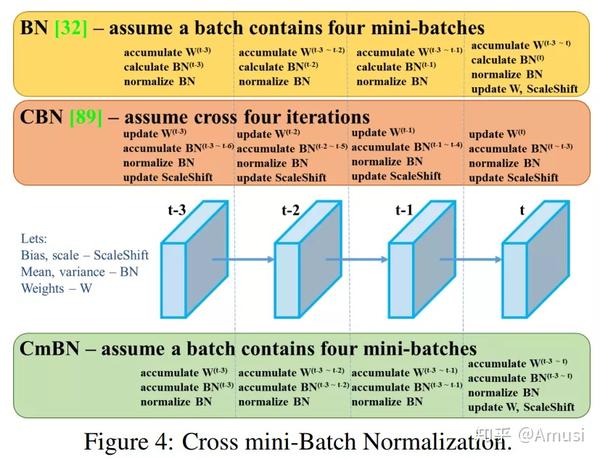
2. 跨批量归一化Cross mini-batch Normalization
3.CIoU loss
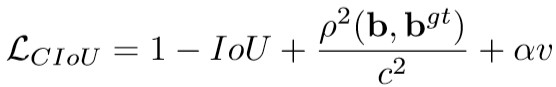
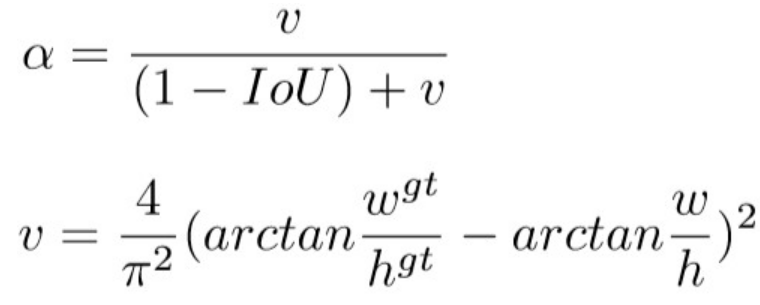
4. class label smoothing
one-hot标签 所存在的disadvantage: 1) 无法保证模型的泛化能力,容易造成过拟合 2)全概率和0概率鼓励所属类别和其他类别之间的差距尽可能加大,而由梯度有界可知这种情况很难adapt,会造成模型过于相信预测的类别.
我们将q(k)改为q(k)' , 即下图所示机制,从而使模型less confident.
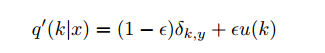
从而,交叉熵为: