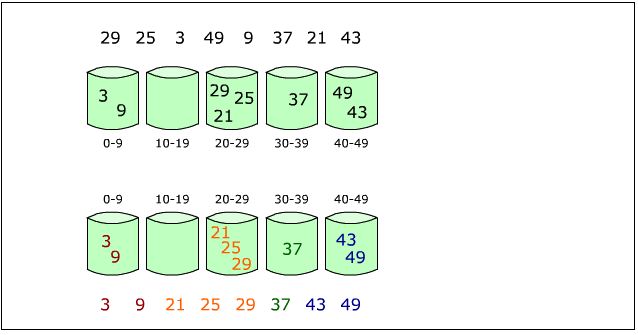
数据结构课程可能会考到的排序算法:
插入排序 希尔排序 冒泡法 快排 选择排序 堆排序 归并排序
一 插入排序

#include<cstdio> #include<string> #include<cstring> #include<iostream> using namespace std; void print(int a[], int n ,int i) { cout<<i <<":"; for(int j= 0; j<8; j++) { cout<<a[j] <<" "; } cout<<endl; } void InsertSort(int a[], int n) { for(int i= 1; i<n; i++){ if(a[i] < a[i-1]){ //若第i个元素大于i-1元素,直接插入。小于的话,移动有序表后插入 int j= i-1; int x = a[i]; //复制为哨兵,即存储待排序元素 a[i] = a[i-1]; //先后移一个元素 while(x < a[j]){ //查找在有序表的插入位置 a[j+1] = a[j]; j--; //元素后移 } a[j+1] = x; //插入到正确位置 } print(a,n,i); //打印每趟排序的结果 } } int main() { int a[8] = {3,1,5,7,2,4,9,6}; InsertSort(a,8); print(a,8,8); return 0; }
如图所示为插入过程各元素依次寻找位置
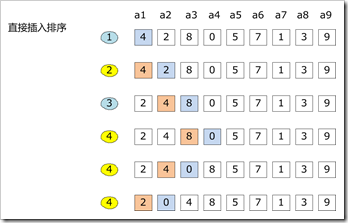
二 希尔排序

#include<cstdio> #include<string> #include<cstring> #include<iostream> using namespace std; void print(int a[], int n ,int i) { cout<<i <<":"; for(int j= 0; j<8; j++) { cout<<a[j] <<" "; } cout<<endl; } /** * 直接插入排序的一般形式 * * @param int dk 缩小增量,如果是直接插入排序,dk=1 * */ void ShellInsertSort(int a[], int n, int dk) { for(int i= dk; i<n; ++i) { if(a[i] < a[i-dk]) //若第i个元素大于i-1元素,直接插入。小于的话,移动有序表后插入 { int j = i-dk; int x = a[i]; //复制为哨兵,即存储待排序元素 a[i] = a[i-dk]; //首先后移一个元素 while(x < a[j]) //查找在有序表的插入位置 { a[j+dk] = a[j]; j -= dk; //元素后移 } a[j+dk] = x; //插入到正确位置 } print(a, n,i ); } } /** * 先按增量d(n/2,n为要排序数的个数进行希尔排序 * */ void shellSort(int a[], int n) { int dk = n/2; while( dk >= 1 ) { ShellInsertSort(a, n, dk); dk = dk/2; } } int main() { int a[8] = {3,1,5,7,2,4,9,6}; //ShellInsertSort(a,8,1); //直接插入排序 shellSort(a,8); //希尔插入排序 print(a,8,8); }
希尔排序如图不断缩小比较规模直到相邻比较

三 冒泡法

#include<cstdio> #include<string> #include<cstring> #include<iostream> using namespace std; void bubbleSort(int a[], int n){ for(int i =0 ; i< n-1; ++i) { for(int j = 0; j < n-i-1; ++j) { if(a[j] > a[j+1]) { int tmp = a[j] ; a[j] = a[j+1] ; a[j+1] = tmp; } } } } void print(int a[], int n ,int i) { cout<<i <<":"; for(int j= 0; j<8; j++) { cout<<a[j] <<" "; } cout<<endl; } int main() { int a[8] = {3,1,5,7,2,4,9,6}; bubbleSort(a,8); print(a,8,8); return 0; }
冒泡法如图所示


四 快速排序

#include<cstdio> #include<string> #include<cstring> #include<iostream> using namespace std; void print(int a[], int n) { for(int j= 0; j<n; j++) { cout<<a[j] <<" "; } cout<<endl; } void swap(int *a, int *b) { int tmp = *a; *a = *b; *b = tmp; } int partition(int a[], int low, int high) { int privotKey = a[low]; //基准元素 while(low < high) { //从表的两端交替地向中间扫描 while(low < high && a[high] >= privotKey) --high; //从high 所指位置向前搜索,至多到low+1 位置。将比基准元素小的交换到低端 swap(&a[low], &a[high]); while(low < high && a[low] <= privotKey ) ++low; swap(&a[low], &a[high]); } print(a,10); return low; } void quickSort(int a[], int low, int high) { if(low < high) { int privotLoc = partition(a, low, high); //将表一分为二 quickSort(a, low, privotLoc -1); //递归对低子表递归排序 quickSort(a, privotLoc + 1, high); //递归对高子表递归排序 } } int main() { int a[10] = {3,1,5,7,2,4,9,6,10,8}; cout<<"初始值:"; print(a,10); quickSort(a,0,9); cout<<"结果:"; print(a,10); return 0; }
快速排序每次比较确定一个位置

五 选择排序

#include<cstdio> #include<string> #include<cstring> #include<iostream> using namespace std; void print(int a[], int n ,int i) { cout<<"第"<<i+1 <<"趟 : "; for(int j= 0; j<8; j++) { cout<<a[j] <<" "; } cout<<endl; } /** * 数组的最小值 * * @return int 数组的键值 */ int SelectMinKey(int a[], int n, int i) { int k = i; for(int j=i+1 ;j< n; ++j) { if(a[k] > a[j]) k = j; } return k; } /** * 选择排序 * */ void selectSort(int a[], int n) { int key, tmp; for(int i = 0; i< n; ++i) { key = SelectMinKey(a, n,i); //选择最小的元素 if(key != i) { tmp = a[i]; a[i] = a[key]; a[key] = tmp; //最小元素与第i位置元素互换 } print(a, n , i); } } int main() { int a[8] = {3,1,5,7,2,4,9,6}; cout<<"初始值:"; for(int j= 0; j<8; j++) { cout<<a[j] <<" "; } cout<<endl<<endl; selectSort(a, 8); print(a,8,8); }
选择排序每次需要扫描一遍剩余序列选出最小(大)的一个放到前面
改进:每趟循环可以确定两个元素(当前趟最大和最小记录)的位置,从而减少排序所需的循环次数。

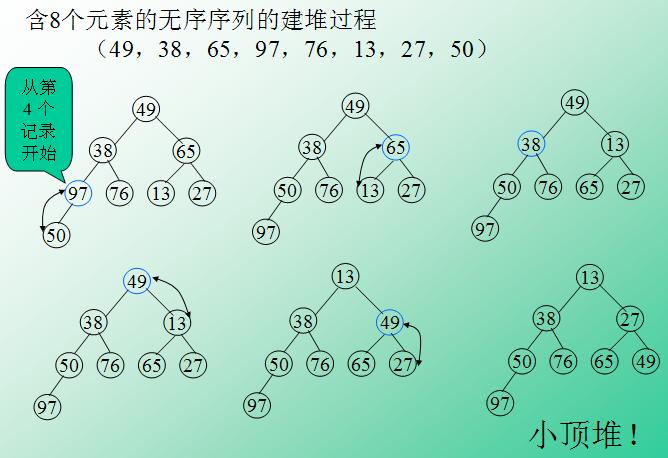
六 堆排序

#include<cstdio> #include<string> #include<cstring> #include<iostream> using namespace std; void print(int a[], int n) { for(int j= 0; j<n; j++) { cout<<a[j] <<" "; } cout<<endl; } /** * 已知H[s…m]除了H[s] 外均满足堆的定义 * 调整H[s],使其成为大顶堆.即将对第s个结点为根的子树筛选, * * @param H是待调整的堆数组 * @param s是待调整的数组元素的位置 * @param length是数组的长度 * */ void HeapAdjust(int H[],int s, int length) { int tmp = H[s]; int child = 2*s+1; //左孩子结点的位置。(i+1 为当前调整结点的右孩子结点的位置) while (child < length) { if(child+1 <length && H[child]<H[child+1]) { // 如果右孩子大于左孩子(找到比当前待调整结点大的孩子结点) ++child ; } if(H[s]<H[child]) // 如果较大的子结点大于父结点 { H[s] = H[child]; // 那么把较大的子结点往上移动,替换它的父结点 s = child; // 重新设置s ,即待调整的下一个结点的位置 child = 2*s+1; } else { // 如果当前待调整结点大于它的左右孩子,则不需要调整,直接退出 break; } H[s] = tmp; // 当前待调整的结点放到比其大的孩子结点位置上 } print(H,length); } /** * 初始堆进行调整 * 将H[0..length-1]建成堆 * 调整完之后第一个元素是序列的最小的元素 */ void BuildingHeap(int H[], int length) { //最后一个有孩子的节点的位置 i= (length -1) / 2 for (int i = (length -1) / 2 ; i >= 0; --i) HeapAdjust(H,i,length); } /** * 堆排序算法 */ void HeapSort(int H[],int length) { //初始堆 BuildingHeap(H, length); //从最后一个元素开始对序列进行调整 for (int i = length - 1; i > 0; --i) { //交换堆顶元素H[0]和堆中最后一个元素 int temp = H[i]; H[i] = H[0]; H[0] = temp; //每次交换堆顶元素和堆中最后一个元素之后,都要对堆进行调整 HeapAdjust(H,0,i); } } int main() { int H[10] = {3,1,5,7,2,4,9,6,10,8}; cout<<"初始值:"; print(H,10); HeapSort(H,10); //selectSort(a, 8); cout<<"结果:"; print(H,10); return 0; }
堆排序是一种树形选择排序,是对直接选择排序的有效改进,可以是小顶堆或者大顶堆。
过程:每次建好堆以后取出堆顶吧叶子放到堆顶重新建堆。
七 归并排序

#include<cstdio> #include<string> #include<cstring> #include<iostream> using namespace std; void print(int a[], int n) { for(int j= 0; j<n; j++) { cout<<a[j] <<" "; } cout<<endl; } //将r[i…m]和r[m +1 …n]归并到辅助数组rf[i…n] void Merge(int *r,int *rf, int i, int m, int n) { int j,k; for(j=m+1,k=i; i<=m && j <=n ; ++k) { if(r[j] < r[i]) rf[k] = r[j++]; else rf[k] = r[i++]; } while(i <= m) rf[k++] = r[i++]; while(j <= n) rf[k++] = r[j++]; print(rf,n+1); } void MergeSort(int *r, int *rf, int lenght) { int len = 1; int *q = r ; int *tmp ; while(len < lenght) { int s = len; len = 2 * s ; int i = 0; while(i+ len <lenght) { Merge(q, rf, i, i+ s-1, i+ len-1 ); //对等长的两个子表合并 i = i+ len; } if(i + s < lenght) { Merge(q, rf, i, i+ s -1, lenght -1); //对不等长的两个子表合并 } tmp = q; q = rf; rf = tmp; //交换q,rf,以保证下一趟归并时,仍从q 归并到rf } } int main() { int a[10] = {3,1,5,7,2,4,9,6,10,8}; int b[10]; MergeSort(a, b, 10); print(b,10); cout<<"结果:"; print(a,10); return 0; }
归并排序将几个有序表合并成一个新的有序表,即把待排序序列分为若干个子序列,每个子序列是有序的。
然后再把有序子序列合并为整体有序序列。

*桶排序

#include<stdio.h> #include<stdlib.h> void bucketSort(double* a,int n)//桶排序 { //链表结点描述 typedef struct Node { double key; struct Node * next; } Node; //辅助数组元素描述 typedef struct { Node * next; } Head; int i,j; Head head[10]= {NULL}; Node * p; Node * q; Node * node; for(i=1; i<=n; i++) { node=(Node*)malloc(sizeof(Node)); node->key=a[i]; node->next=NULL; p = q =head[(int)(a[i]*10)].next; if(p == NULL) { head[(int)(a[i]*10)].next=node; continue; } while(p) { if(node->key < p->key) break; q=p; p=p->next; } if(p == NULL) { q->next=node; } else { node->next=p; q->next=node; } } j=1; for(i=0; i<10; i++) { p=head[i].next; while(p) { a[j++]=p->key; p=p->next; } } } int main() { int i; double a[13]= {0,0.13,0.25,0.18,0.29,0.81,0.52,0.52,0.83,0.52,0.69,0.13,0.16}; //不考虑a[0] bucketSort(a,12); for(i=1; i<=12; i++) printf("%-6.2f",a[i]); printf(" "); return 0; return 0; }
桶排序效率高稳定,流程见图