Description
【背景介绍】
古堡,暗鸦,斜阳,和深渊……
等了三年,我独自一人,终于来到了这里……
“终焉的试炼吗?就在这里吗?”我自言自语道。
“终焉的试炼啊!就在这里啊!”我再一次自言自语道。
“这背后可能有那个东西吗?”我自言自语道。
“这背后一定有那个东西呢!”我又一次自言自语道。
我沉默着,踏上黑漆漆的索桥,小心翼翼地,拿出锋利的注入我灵魂的双剑……
“那么,我们开始吧……”我最后一次自言自语道。
【题目描述】
My soul of my sowrd!
终焉的试炼即将到来,作为一名有修养的剑士,虽然没有习得n刀流但是二刀流还是没问题的。然而我也是个剑的收藏者,家里屯着n把剑,每一把剑都有一个灵魂值a[i],由于一些剑之间可能有共鸣,所以我需要两把契合度最高的剑。据剑圣所说,两把编号为i,j剑的契合度为a[i] and a[j]。如何深得剑的灵魂呢?
注:AND 为按位与运算,先将数转成二进制,不满位数的补全0,然后成为两个长度相同的二进制数,处理的时候,两个相应的二进制位都为1,该位的结果值才为1,否则为0。例下图。

Input
第一行一个整数n,代表藏剑数。
第二行n个整数,第i个整数表示a[i]。
Output
输出包含一个正整数,最好的两把剑的契合度。
Sample Input
5
12 5 6 3 1
Sample Output
4
【样例解释】
5 and 6=4或者12 and 5=4或者12 and 6=4
Data Constraint
对于40%的数据 n ≤ 1,000
对于100%的数据 n ≤ 1,000,000,0 ≤ a[i] < 2^31
solution
对于40%的数据
时间复杂度:
直接暴力两两判断
对于100%的数据
1.先sort然后前后两两判断
时间复杂度: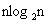
显然错误,但是数据太水了。。。
2.暴力基础上用ans优化
还是数据太水了。。。
正解
先考虑答案的性质:
Ans=a1*2^0+a2*2^1+a3*2^a3+…….+an*2^(n-1);
可见,答案中吗,高位的数选肯定比不选优。
那我们就考虑答案的倒数第i位是否可以选。
设当前Ans为比第i位高的所有二进制位选择的最优情况的和,那么如果第i位能选,就必定在这n个数中至少有两个数满足:
1:当前答案中的所有二进制为1的位置,在相应的这个数中的位置也为1(即ans and a=ans);
2:这个数的二进制第i位为1(即a and (2^(i-1)=(2^(i-1)))。
所以,我们只需从高位向低位扫一遍就可以了。
时间:O(30*n)
空间:n
rethink
对二进制还是不够熟练
大致思路没问题
但是WA了两个点
看到数据这么水我都怀疑我是不是错的。。。
1 void violence() 2 { 3 for(R int i = 1; i <= n; i++) read(a[i]); 4 for(R int i = 1; i <= n; i++) 5 for(R int j = i + 1; j <= n; j++) 6 ans = max(ans, a[i] & a[j]); 7 writeln(ans); 8 } 9 bool cmp(int a, int b) 10 { 11 return a > b; 12 } 13 int count(int x) 14 { 15 int k = 0; 16 while(x) 17 { 18 k++; 19 x >>= 1; 20 } 21 return k; 22 } 23 int and1(int x) 24 { 25 return ((1 << x) - 1); 26 } 27 void work() 28 { 29 for(R int i = 1; i <= n; i++) read(a[i]); 30 do 31 { 32 sort(a + 1, a + n + 1, cmp); 33 int ii = 1; 34 while(count(a[ii]) != count(a[ii + 1]) && ii + 1 <= n) ii++; 35 //printf("%lld ",ii); 36 if(ii != 1) 37 { 38 int qwq = count(a[ii]); 39 //writeln(qwq); 40 int cut = and1(qwq); 41 for(R int i = 1; i <= ii - 1; i++) a[i] = a[i] & cut; 42 //for(R int i = 1; i <= n; i++) writesn(a[i]); 43 //putchar(' '); 44 //writeln(n); 45 continue; 46 } 47 int k = count(a[1]); 48 for(R int i = 3; i <= n; i++) 49 if(count(a[i]) != k) 50 { 51 n = i - 1; 52 break; 53 } 54 book[k] = 1; 55 for(R int i = 1; i <= n ; i++) a[i] -= (1 << (k - 1)); 56 }while(a[1]); 57 for(R int i = 1; i <= 31; i++) if(book[i]) ans += (1 << (i - 1)); 58 writeln(ans); 59 } 60 signed main() 61 { 62 //freopen("sword.in","r",stdin); 63 //freopen("sword.out","w",stdout); 64 read(n); 65 if(n <= 5000) 66 { 67 violence(); 68 return 0; 69 } 70 work(); 71 return 0; 72 }
code
1 #include<iostream> 2 #include<cstdio> 3 #include<cmath> 4 #include<algorithm> 5 #include<cstring> 6 #include<queue> 7 #include<vector> 8 #include<stack> 9 #include<set> 10 #include<deque> 11 #include<map> 12 using namespace std; 13 14 template <typename T> void read(T &x) { 15 x = 0; int f = 1; char c; 16 for (c = getchar(); c < '0' || c > '9'; c = getchar()) if (c == '-') f = -f; 17 for (; c >= '0' && c <= '9'; c = getchar()) x = 10 * x + c - '0' ; 18 x *= f; 19 } 20 template <typename T> void write(T x){ 21 if (x < 0) putchar('-'), x = -x; 22 if (x > 9) write(x / 10); 23 putchar(x % 10 + '0'); 24 } 25 template <typename T> void writeln(T x) { write(x); putchar(' '); } 26 template <typename T> void writesn(T x) { write(x); putchar(' '); } 27 28 #define ll long long 29 #define inf 1234567890 30 #define next net 31 #define P 2147483647 32 #define N 1000010 33 #define mid ((l+r)>>1) 34 #define lson (o<<1) 35 #define rson (o<<1|1) 36 #define R register 37 #define debug puts("zxt") 38 39 int n, ans; 40 int a[1000010]; 41 signed main() 42 { 43 //freopen("sword.in","r",stdin); 44 //freopen("sword.out","w",stdout); 45 read(n); 46 for(R int i = 1; i <= n; i++) read(a[i]); 47 for(R int i = 31; i >= 1; i--) 48 { 49 int t = 0; 50 for(R int j = 1; j <= n; j++) 51 if(((ans & a[j]) == ans) && ((a[j] & (1 << (i - 1))) != 0)) t++; 52 if(t >= 2) ans += (1 << (i - 1)); 53 } 54 writeln(ans); 55 return 0; 56 }