特征分解：将矩阵分 解成一组特征向量和特征值。
方阵 A 的 特征向量(eigenvector)是指与 A 相乘后相当于对该向量进行缩放 的非零向量 v
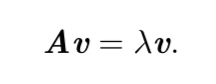
标量 λ 被称为这个特征向量对应的 特征值(eigenvalue)。(类似地，我们也可以
定义 左特征向量(left eigenvector)v⊤A = λv⊤，但是通常我们更关注 右特征向量 (right eigenvector))
如果V是A的特征向量，那么任何放缩后的 sv (s为任意非零实数)也是A的特征向量，所以A的特征向量我们只考虑单位特征向量。假设矩阵A有n个线性无关的特征向量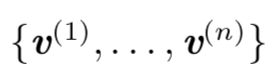
，对应着特征值
类似地，我们也可以将特征值连接成一个向量 λ = [λ1, . . . , λn]⊤。 因此 A 的 特征分解(eigendecomposition)可以记作
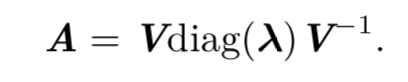
所有特征值都是正数的矩阵被称为 正定(positive definite);所有特征值都是非 负数的矩阵被称为 半正定(positive semidefinite)。同样地，所有特征值都是负数的 矩阵被称为 负定(negative definite);所有特征值都是非正数的矩阵被称为 半负定
(negative semidefinite)。半正定矩阵受到关注是因为它们保证 ∀x, x⊤Ax ≥ 0。此外， 正定矩阵还保证 x⊤Ax = 0 ⇒ x = 0。
接下来说些在知乎上看到的一些对特征值分解含义的一些看法：如果把矩阵看作是运动的话，特征值表示速度的大小，特征向量表示运动的方向
特征值分解是针对于方阵的，应用有PCA降维，数据压缩（比如图片的压缩）。
奇异值分解，是特征值分解更一般的情况。奇异值分解的应用有推荐系统，数据压缩。
通过奇异值分解，我 们会得到一些与特征分解相同类型的信息。然而，奇异值分解有更广泛的应用。每 个实数矩阵都有一个奇异值分解，但不一定都有特征分解。
奇异值分解是类似的，只不过这回我们将矩阵 A 分解成三个矩阵的乘积:
A = UDV⊤
参考资料：
https://www.zhihu.com/question/21874816