
壹 ❀ 引
在最近的工作中,有一个任务是需要修复富文本编辑器字号显示的BUG。大概情况就是,从WPS中复制不同样式的标题、正文到到项目编辑器中,发现没办法设置选中的文本为正文;而且字体字号都显示为默认的情况下,这些字体大小还表现不同。因为该富文本编辑器是基于ckeditor二次开发,所以也是看了一天的源码才成功定位到问题,最后发现WPS的字体单位使用的是印刷行业的单位,也就是pt,而不是我们熟知的px,这就导致了富文本编辑器无法识别该pt单位,从而产生了后续一系列的bug。
经过与程序原作者沟通讨论,最终确定的修复方案是将WPS粘贴过来的文本原数据进行单位换算加工。其次还有一个问题,编辑器的字号大小选择范围一般是间断的而非连续的,比如下图:
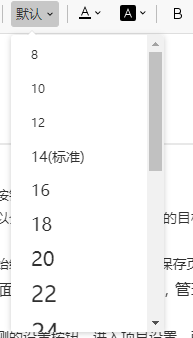
如果编辑器能展示的字号范围未能匹配到我们最终拿到的字号大小,那么编辑器就会展示字号为默认,因为匹配不到,那这样就还是会造成13px与15px都显示为默认的情况,从而给了用户一种字号都是默认,但字体大小显示不同的疑问。所以我们在换算之后还多了一步操作,我们需要在编辑器的字号范围中找到与换算后的字号最接近的数字,作为最终展示字体大小,那么这就衍生出了一个问题,怎么在数组中找到与目标数字最为接近的数字。
贰 ❀ 尝试解决
归纳上面的问题,其实就是在一个数组中找到与目标数字最近接的数字,比如:
const arr = [1,3,5,6,10];
const target = 7;
// 最终找到6,因为7和6的差最小
const arr = [1,3,5,6,10];
const target = 3;
// 最终找到3,还有比相等的数字更为接近的?
只要简单分析上述两个例子,我们要找的值其实就是与目标值target的差最小的一个数,考虑到存在差为负数的情况,所以这个差应该是一个绝对值,可用abs()转换。那么我们来尝试实现它:
const arr = [1, 2, 6, 10, 9];
const target = 3;
const findNearestNumber = (arr, target) => {
// 我们假设最近接的就是数组第第一个数字
let result = arr[0];
for (let i = 1, len = arr.length; i < len; i++) {
if (Math.abs(arr[i] - target) < Math.abs(result - target)) {
result = arr[i];
};
};
return result;
};
console.log(findNearestNumber(arr, target));//2
让我们回顾上述代码,一开始,我们需要提供一个初始值,并拿下一个值参与比较之后决定返回两者中的某一个值,然后继续参与后续遍历,仔细一想,这不就是在做reduce的操作吗,所以我们简化下代码,变成了这样:
const findNearestNumber = (arr, target) => {
return arr.reduce((pre, curr) => {
return Math.abs(pre - target) > Math.abs(curr - target) ? curr : pre;
})
};
以上的实现适用于有序以及无序数组,考虑无序的情况,我们最差的情况就是完整遍历一遍,最终发现最后一个数字才是我们想要的,所以站在时间复杂度上来说就是O(n)。
不过我们现在的需求有点不同,很明显字号大小是从小到大排列的,比如这样一个数组:
const fontSize = [8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 36, 48, 72];
这是一个有序数组,就像肌肉记忆一样,看到有序数组,谈到遍历我们首先想到的就应该是二分查找,其实上篇文章我也提过公司code review会比较严格,对于性能要求比较高。发版那天本来就够忙了,我可不想在提测通过后,因为review没过,又得修改代码再次走测试流程,非常费时,所以保险起见,这里就直接考虑二分查找来做了。
我们声明左右两个指针,分别指向数组的第0位索引和最后一位索引,然后求出中间索引,拿中间索引所对应的数字与target对比,如果target比arr[mid]大,那说明target肯定在右边范围,这时候只要修改左指针为mid即可,反之修改右指针。
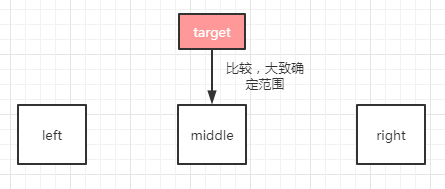
因为目标值不存在于数组中,所以最终我们得保证左右指针指到相邻的两个数字上,大致实现如下:
const findNearesttargetber = (arr, target) => {
let mid;
let l = 0;
let r = arr.length - 1;
// 保证指针最终停留在相邻的两个数,所以这里是判断是否大于1
while (r - l > 1) {
mid = Math.floor((l + r) / 2);
// 如果目标数比中间小,所以范围在左边
if (target < arr[mid]) {
r = mid;
} else {
l = mid;
};
};
// 最后比较这两个数字的绝对差大小即可。
return Math.abs(target - arr[l]) <= Math.abs(target - arr[r]) ? arr[l] : arr[r];
}
由于二分查找每次都能排除掉一半的可能,所以时间复杂度为O(logn),当然由于当前数组并不是很庞大,执行上其实也并不太大区别,只是尽可能去这么写了。那么关于本文就到这里了。