单层感知器属于单层前向网络,即除输入层和输出层之外,只拥有一层神经元节点。
特点:输入数据从输入层经过隐藏层向输出层逐层传播,相邻两层的神经元之间相互连接,同一层的神经元之间没有连接。
感知器(perception)是由美国学者F.Rosenblatt提出的。与最早提出的MP模型不同,神经元突触权值可变,因此可以通过一定规则进行学习。可以快速、可靠地解决线性可分的问题。
单层感知器由一个线性组合器和一个二值阈值元件组成。
输入是一个N维向量 x=[x1,x2,...,xn],其中每一个分量对应一个权值wi,隐含层输出叠加为一个标量值:
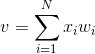
随后在二值阈值元件中对得到的v值进行判断,产生二值输出:
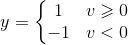
可以将数据分为两类。实际应用中,还加入偏置,值恒为1,权值为b。这时,y输出为:
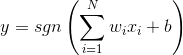
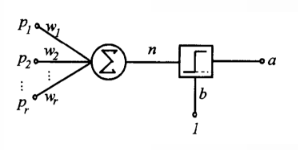
单层感知器结构图:
单层感知器进行模式识别的超平面由下式决定:
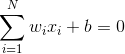
当维数N=2时,输入向量可以表示为平面直角坐标系中的一个点。此时分类超平面是一条直线:
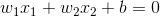
这样就可以将点沿直线划分成两类。
二、学习算法步骤:
(1)定义变量和参数。
x(n)=N+1维输入向量=[+1,x1(n),x2(n),...,xN(n)]T
w(n)=N+1维权值向量=[b(n),w1(n),w2(n),...,wN(n)]T
b(n)=偏置
y(n)=实际输出
d(n)=期望输出
η(n)=学习率参数,是一个比1小的正常数
(2)初始化。n=0,将权值向量w设置为随机值或全零值。
(3)激活。输入训练样本,对每个训练样本x(n)=[+1,x1(n),x2(n),...,xN(n)]T,指定其期望输出d,(我认为是训练阶段)
(4)计算实际输出。 y(n)=sgn(wT(n)x(n))
(5)更新权值向量 w(n+1)=w(n)+η[d(n)-y(n)]x(n)
这里
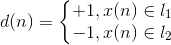
0<η<1
(6)判断。若满足收敛条件,则算法结束,若不满足,n++,转到第(3)步。
收敛条件:当权值向量w已经能正确实现分类时,算法就收敛了,此时网络误差为零。收敛条件通常可以是:
误差小于某个预先设定的较小的值ε。即
|d(n)-y(n)|<ε
两次迭代之间的权值变化已经很小,即
|w(n+1)-w(n)|<ε
设定最大迭代次数M,当迭代了M次就停止迭代。
需事先通过经验设定学习率η,不应该过大,以便为输入向量提供一个比较稳定的权值估计。不应过小,以便使权值能根据输入的向量x实时变化,体现误差对权值的修正作用。
它只对线性可分的问题收敛,通过学习调整权值,最终找到合适的决策面,实现正确分类。
三、感知器的局限性
(1)感知器的激活函数使用阈值函数,使得输出只能取两个值(-1/1或0/1)
(2)只对线性可分的问题收敛
(3)如果输入样本存在奇异样本,则网络需要花费很长时间。(奇异样本是数值上远远偏离其他样本的数据)
(4)感知器的学习算法只对单层有效,因此无法套用其规则设计多层感知器。
四、单层感知器相关函数详解
newp--创建一个感知器
net=newp(P,T,TF,LF)
P是一个R*2矩阵,矩阵行数R等于输入向量的维数。R行就输入R个分量向量,2代表范围,如P=[-1,1;0,1]就是每个输入向量输入两个分量向量,范围-1~1,0~1。
T表示输出节点的个数,标量
TF,传输函数。可取值为hardlim或hardlims,默认为hardlim。
hardlims: 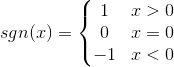
hardlim:遇到负数,输出值为0而不是-1。
LF:学习函数,可取值为learnp或learnpn,默认值learnp 输入向量数值幅度变化较大时,采用learnpn代替learnp,可以加快计算速度。
net:返回的感知器网络。
train--训练感知器网络
[net,tr]=train(net,P,T,Pi,Ai)
net:需要训练的神经网络
P:网络输入。P是R*Q输入矩阵,每一列是一个输入向量,R为输入节点个数(维数,比如输入一组XY坐标,R为2,一次输入2个数),Q列就是Q个训练输入向量。
T:网络期望输出。与P同理。
Pi:初始输入延迟,默认0
Ai:初始的层延迟,默认0
net:训练好的网络
tr:训练记录,包括训练步数epoch和性能perf。
对于没有输入延迟或者层延迟的网路。Pi,Ai,Pf和Af是不需要的。
sim--对训练好的网络进行仿真
[Y,Pf,Af,E,perf]=sim(net,P,Pi,Ai)
P:网络输入同上。
Pi初始输出延迟 Pf最终输出延迟
Ai初始层延迟 Af最终层延迟
Y:网络对输入P的实际输出
E: 网络误差
perf:网络的性能
用Y=net(P)可以得到与用sim函数相同的结果。
init--神经网络初始化
net=init(net)
可以查询net.iw(1,1)
可以查询net.b(1)
adapt--神经网络的自适应
[net,Y,E,Pf,Af,tr]=adapt(net,P,T,Pi,Ai)
调整神经网络误差
ma=mae(E) 平均绝对误差。