shaderToy学习篇

觉得shadertoy上的一些网友的作品写得很好，加上自己对glsl一些内置函数，内置变量不是很熟悉，于是决定开始学习一下上面一些大佬的代码。

今天的案例是这个：

附上shaderToy的地址：https://www.shadertoy.com/view/ll2GD3

用three.js的ShaderMaterial实现的着色器代码如下：

<script id="vertex-shader-1" type="x-shader/x-vertex">
    void main(){
        gl_Position = projectionMatrix * modelViewMatrix * vec4(position,1.0);
    }
</script>


<script id="fragment-shader-9" type="x-shader/x-fragment">
    uniform vec2 resolution;

    vec3 pal( in float t, in vec3 a, in vec3 b, in vec3 c, in vec3 d ){
        return a + b*cos( 6.28318*(c*t+d) );
    }
    void main( void ) {
        vec2 p = gl_FragCoord.xy / resolution.xy;
        vec3 col = pal( p.x, vec3(0.5,0.5,0.5),vec3(0.5,0.5,0.5),vec3(1.0,1.0,1.0),vec3(0.0,0.33,0.67) );
        if( p.y>(1.0/7.0) ) col = pal( p.x, vec3(0.5,0.5,0.5),vec3(0.5,0.5,0.5),vec3(1.0,1.0,1.0),vec3(0.0,0.10,0.20) );
        if( p.y>(2.0/7.0) ) col = pal( p.x, vec3(0.5,0.5,0.5),vec3(0.5,0.5,0.5),vec3(1.0,1.0,1.0),vec3(0.3,0.20,0.20) );
        if( p.y>(3.0/7.0) ) col = pal( p.x, vec3(0.5,0.5,0.5),vec3(0.5,0.5,0.5),vec3(1.0,1.0,0.5),vec3(0.8,0.90,0.30) );
        if( p.y>(4.0/7.0) ) col = pal( p.x, vec3(0.5,0.5,0.5),vec3(0.5,0.5,0.5),vec3(1.0,0.7,0.4),vec3(0.0,0.15,0.20) );
        if( p.y>(5.0/7.0) ) col = pal( p.x, vec3(0.5,0.5,0.5),vec3(0.5,0.5,0.5),vec3(2.0,1.0,0.0),vec3(0.5,0.20,0.25) );
        if( p.y>(6.0/7.0) ) col = pal( p.x, vec3(0.8,0.5,0.4),vec3(0.2,0.4,0.2),vec3(2.0,1.0,1.0),vec3(0.0,0.25,0.25) );
        // band
        float f = fract(p.y*7.0);
        // borders
        col *= smoothstep( 0.49, 0.47, abs(f-0.5) );
        // shadowing
        col *= 0.5 + 0.5*sqrt(4.0*f*(1.0-f));
    
        gl_FragColor = vec4(col,1.0);
    }
</script>

参数说明：

resolution：传入的一个vec2，其实就是画布的大小(width,height).

代码解析：

1⃣️画布归一化

vec2 p = gl_FragCoord.xy / resolution.xy;

上述代码的作用是，使得画布上的任意一点p的横轴值范围和纵轴值范围都是[0,1]，极大地方便了后续色值的计算，因为色值每个通道的值范围也是[0,1]

 2⃣️y轴分块，x轴颜色渐变

不难看出，分成了7等份

针对每单独的一份呢，y轴颜色不做区分，x轴颜色渐变，并且是与x轴值相关，相关代码如下：

    vec3 pal( in float t, in vec3 a, in vec3 b, in vec3 c, in vec3 d ){
        return a + b*cos( 6.28318*(c*t+d) );
    }

该函数有4个形参，分别是t(x轴坐标值，注意x的范围此时是0到1)和自定义的4种颜色。

后面的三角函数可以看作 y = b * cos(k(c*x + d))，所以y的值范围是[-b,b],那么颜色3个通道的值肯定不能小于0啊，最好也是不能大于1的,所以在前面补上a，

并且a-b>0;a+b<1;

解该二元一次不等式得:

b<0.5,

然后我们再来看一下代码中计算颜色时给的实参：

对于每个维度来说，也确实是a > b的。

补充:对于a、b,每个维度之和小于等于1,

3⃣️加边框

        // band
        float f = fract(p.y*7.0);
        // borders
        col *= smoothstep( 0.49, 0.47, abs(f-0.5) );

我刚开始想的时候，是想着用透明度做的,看到了作者的代码,又见到这个smoothstep函数,于是去详细了解了一下:

图示法如下:

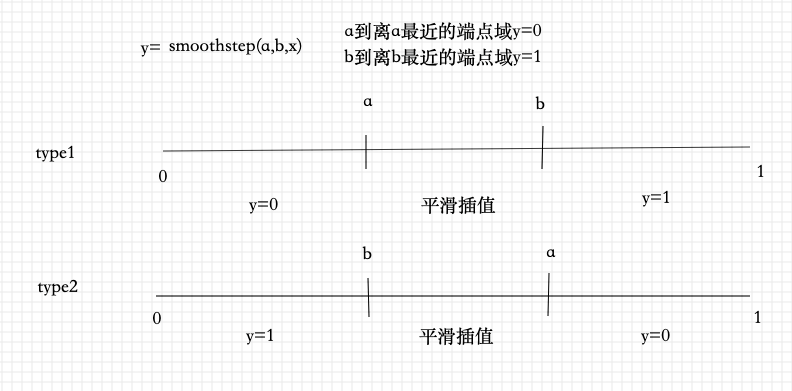
所以,针对上述代码,first:

float f = fract(p.y*7.0);

p.y * 7.0 的值为0.1、0.2、...1.0、1.1、1.2、...2.0、2.1、2.2、...3.0、3.1、3.2、........6.0、6.1、6.2、...7.0;

fract是取小数函数,所以对于每一段的f值范围都是0.0、0.1、0.2、0.3、0.4、0.5....0.9、0.0;

smoothstep( 0.49, 0.47, abs(f-0.5) )

abs(f-0.5) 走势是这样的(绝对值):0.5、0.4、0.3、0.2、0.1、0.0、0.1、0.2、0.3、0.4、0.5;

0.49 > 0.47,就是a > b;符合上述第二种计算规则,

所以该函数式算得的值走势是:0->平滑插值(升)->1->平滑插值(降)->0

col *= smoothstep( 0.48, 0.47, abs(f-0.5) );

所以在y轴上,之前的满屏,现在有了缝隙,效果如下:

因为末端smoothstep函数值为0,算得颜色为rgb(0.,0.,0.)

4⃣️smoothstep函数处理获得其他效果

float f = fract(p.y*7.0);
abs(f-0.5)

abs最大值为0.5,所以只要smoothstep(a,b,x)中

a>b,并且

a>0.5,就不会出现缝隙;

b<0.5,才会有平滑效果.

    col *= smoothstep( 0.98, 0.07, abs(f-0.5) );

smoothstep:

效果如下:

col *= smoothstep( 0.98, 0.37, abs(f-0.5) );

smoothstep:

效果如下:

 5⃣️sqrt(x * (1-x))实现y轴弧形渐变

首先看一下y = 0.5 + sqrt(x * (1-x))的表示的图形

所以对于着色器代码:

col *= 0.5 + 0.5*sqrt(4.0*f*(1.0-f));

转化为:

col *= 0.5 + sqrt(f*(1.0-f));

因为f变化顺序为0.5->0.0->0.5;所以对照上面的图形,y轴颜色的被乘数变化为1.0->0.5->1.0,注意这些变化为非线性的,所以y轴变化如下:

再乘一次:

col *= 0.5 + sqrt(f*(1.0-f));

继续:

继续: