K近邻（K Nearest Neighbor-KNN）原理讲解及实现

算法原理

---

K最近邻（k-Nearest Neighbor）算法是比较简单的机器学习算法。它采用测量不同特征值之间的距离方法进行分类。它的思想很简单：如果一个样本在特征空间中的k个最近邻（最相似）的样本中的大多数都属于某一个类别，则该样本也属于这个类别。第一个字母k可以小写，表示外部定义的近邻数量。

举例说明

---

首先我们准备一个数据集，这个数据集很简单，是由二维空间上的4个点构成的一个矩阵，如表1所示：

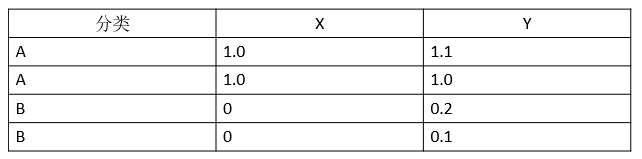
                                                                 表1：训练集

其中前两个点构成一个类别A，后两个点构成一个类别B。我们用Python把这4个点在坐标系中绘制出来，如图1所示：

                                                                                       图1：训练集绘制

绘制所用的代码如下：

# -*- encoding:utf-8-* -
from numpy import *
import matplotlib.pyplot as plt

def createDataSet():
    dataSet = array([[1.0, 1.1], [1.0, 1.0], [0, 0.2], [0, 0.1]])  # 数据集
    labels = ['A', 'A', 'B', 'B']  # 数据集对应的类别标签
    return dataSet, labels

dataSet, labels = createDataSet()
# 显示数据集信息
fig = plt.figure()
ax = fig.add_subplot(111)
indx = 0
for point in dataSet:
    if labels[indx] == 'A':
        ax.scatter(point[0], point[1], c='blue', marker='o', linewidths=0, s=300)
        plt.annotate("("+str(point[0])+","+str(point[1])+")", xy=(point[0], point[1]))
    else:
        ax.scatter(point[0], point[1], c='red', marker='^', linewidths=0, s=300)
        plt.annotate("("+str(point[0])+","+str(point[1])+")", xy=(point[0], point[1]))
    indx += 1
plt.show()

从图形中可以清晰地看到由4个点构成的训练集。该训练集被分为两个类别：A类——蓝色圆圈，B类——红色三角形。因为红色区域内的点距比它们到蓝色区域内的点距要小的多，这种分类也很自然。
下面我们给出测试集，只有一个点，我们把它加入到刚才的矩阵中去，如表2所示：

                                                          表2：加入了一个训练样本

我们想知道给出的这个测试集应该属于哪个分类，最简单的方法还是画图，我们把新加入的点加入图中，图2很清晰，从距离上看，它更接近红色三角形的范围，应该归于B类，这就是KNN算法的基本原理。

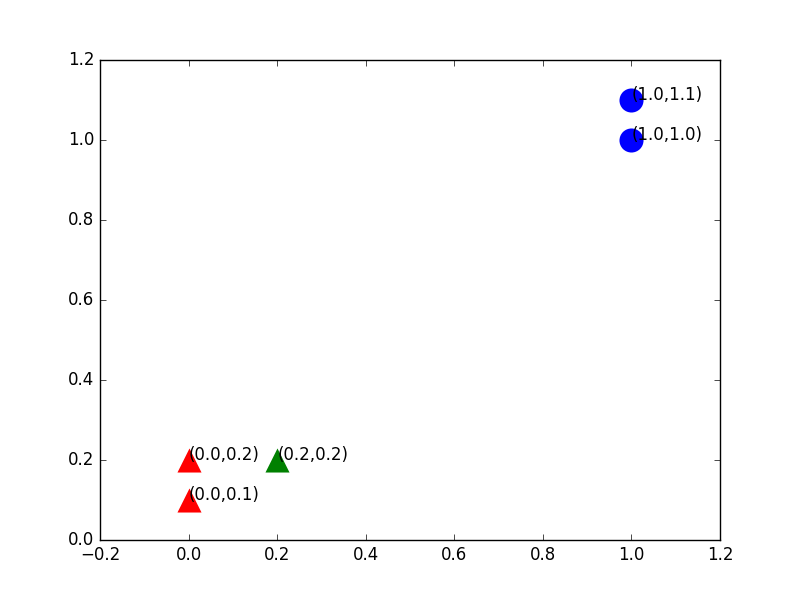
                                                                图2：加入一个训练样本后绘制

在上述代码的基础上，绘制测试样本点的代码如下：

# 显示即将需要测试的数据信息
testdata = [0.2, 0.2]
ax.scatter(testdata[0], testdata[1], c='green', marker='^', linewidths=0, s=300)
plt.annotate("(" + str(testdata[0]) + "," + str(testdata[1]) + ")", xy=(testdata[0], testdata[1]))
plt.show()

算法实现

---

综上所述，KNN算法应由以下步骤构成。
第一阶段：确定k值（就是指最近邻居的个数）。一般是一个奇数，因为测试样本有限，故取值为3。
第二阶段：确定距离度量公式。文本分类一般使用夹角余弦，得出待分类数据点和所有已知类别的样本点，从中选择距离最近的k个样本。
夹角余弦：

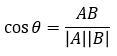
第三阶段：统计这k个样本点中各个类别的数量。上例中我们选定k值为3，则B类样本（三角形）有2个，A类样本（圆形）有 1个，那么我们就把这个方形数据点定位B类；即，根据k个样本中数量最多的样本是什么类别，我们就把这个数据点定为什么类别。

实现代码如下：

from numpy import *
import operator

# 产生数据集
def createDataSet():
    dataSet = array([[1.0, 1.1], [1.0, 1.0], [0, 0.2], [0, 0.1]])  # 数据集
    labels = ['A', 'A', 'B', 'B']  # 数据集对应的类别标签
    return dataSet, labels

# 夹角余弦距离公式
def cosdist(vector1, vector2):
    return dot(vector1, vector2) / (linalg.norm(vector1) * linalg.norm(vector2))

# KNN 分类器
# 测试集：testdata； 训练集：trainSet；类别标签：listClasses；k: k个邻居数
def classify(testdata, trainSet, listClasses, k):
    dataSetSize = trainSet.shape[0]  # 返回样本集的行数
    distances = array(zeros(dataSetSize))
    for indx in xrange(dataSetSize):   # 计算测试集与训练集之间的距离：夹角余弦
        distances[indx] = cosdist(testdata, trainSet[indx])
    # 根据生成的夹角余弦按从小到大排序，结果为索引号
    sortedDistIndicies = argsort(distances)
    classCount = {}
    for i in range(k):
        # 按排序顺序返回样本集对应的类别标签
        voteIlabel = listClasses[sortedDistIndicies[i]]
        # 为字典classCount赋值，相同的key，value加1
        classCount[voteIlabel] = classCount.get(voteIlabel, 0) + 1
    # sorted():按字典值进行排序，返回list
    sortedClassCount = sorted(classCount.iteritems(), key=operator.itemgetter(1), reverse=True)
    return sortedClassCount[0][0]

# dataSet:测试数据集
# labels：测试数据集对应的标签
dataSet, labels = createDataSet()
testdata = [0.2, 0.2]
k = 3   # 选取最近的K个样本进行类别判定
# 判定testdata类别，输出类别结果
print "label is: " + classify(testdata, dataSet, labels, k)

输出：“label is: B“