题目地址:
题目概要:某个高中有80名学生,其中40名得到了大学的录取,40名没有被录取。x中包含80名学生两门标准考试的成绩,y中包含学生是否被录取(1代表录取、0代表未录取)。
过程:
1、加载试验数据,并为x输入添加一个偏置项。
x=load('ex4x.dat'); y=load('ex4y.dat'); x=[ones(length(y),1) x];
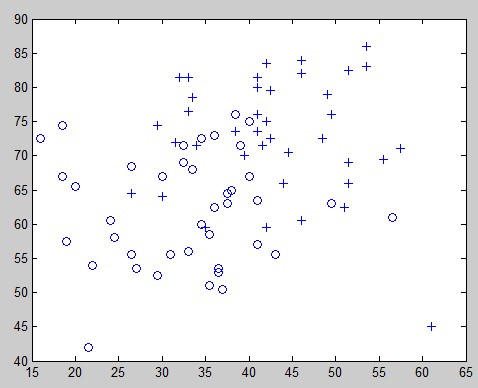
2、绘制数据分布
% find returns the indices of the % rows meeting the specified condition pos = find(y == 1); neg = find(y == 0); % Assume the features are in the 2nd and 3rd % columns of x plot(x(pos, 2), x(pos,3), '+'); hold on plot(x(neg, 2), x(neg, 3), 'o')
3、Newton's method
先回忆一下logistic regression的假设:
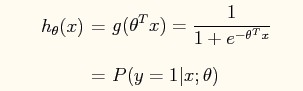
因为matlab中没有sigmoid函数,因此我们用niline定义一个:
g = inline('1.0 ./ (1.0 + exp(-z))'); % Usage: To find the value of the sigmoid % evaluated at 2, call g(2)
再来看看我们定义的cost function J(θ):
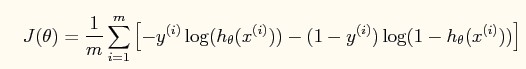
我们希望使用Newton's method来求出cost function J(θ)的最小值。回忆一下Newton's method中θ的迭代规则为:

在logistic regression中,梯度和Hessian的求法分别为:

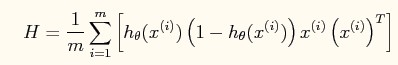
需要注意的是,上述公式中的写法为向量形式。
其中,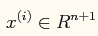 为n+1 * 1的向量,
为n+1 * 1的向量,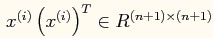 为n+1 * n+1的矩阵。
为n+1 * n+1的矩阵。
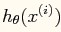 和
和 为标量。
为标量。
实现
按照上述Newton's method所述的方法逐步实现。代码如下
function [theta, J ] = newton( x,y ) %NEWTON Summary of this function goes here % Detailed explanation goes here m = length(y); theta = zeros(3,1); g = inline('1.0 ./ (1.0 + exp(-z))'); pos = find(y == 1); neg = find(y == 0); J = zeros(10, 1); for num_iterations = 1:10 %计算实际输出 h_theta_x = g(x * theta); %将y=0和y=1的情况分开计算后再相加,计算J函数 pos_J_theta = -1 * log(h_theta_x(pos)); neg_J_theta = -1 *log((1- h_theta_x(neg))); J(num_iterations) = sum([pos_J_theta;neg_J_theta])/m; %计算J导数及Hessian矩阵 delta_J = sum(repmat((h_theta_x - y),1,3).*x); H = x'*(repmat((h_theta_x.*(1-h_theta_x)),1,3).*x); %更新θ theta = theta - inv(H)*delta_J'; end % now plot J % technically, the first J starts at the zero-eth iteration % but Matlab/Octave doesn't have a zero index figure; plot(0:9, J(1:10), '-') xlabel('Number of iterations') ylabel('Cost J') end
PS:在练习的附录答案中给出的直接计算J函数的代码很优雅:
J(i) =(1/m)*sum(-y.*log(h) - (1-y).*log(1-h));
在matlab中调用:
[theta J] = newton(x,y);
可以得到输出:
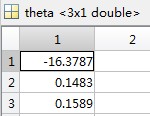
θ为:
J函数输出图像为(令迭代次数为10的情况下):
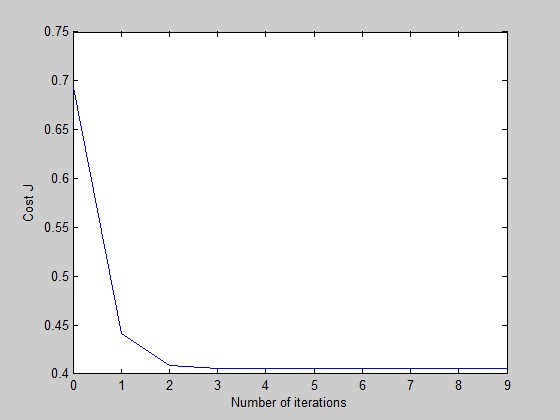
可以看到,其实在迭代至第四次时,就已经收敛了。
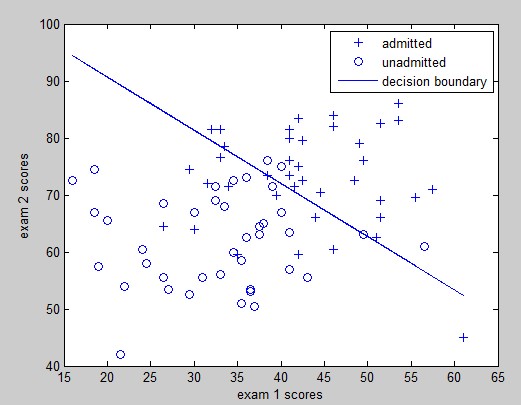
我们可以输出一下admitted和unadmitted的分界线,代码如下:
plot(x(pos, 2), x(pos,3), '+'); hold on plot(x(neg, 2), x(neg, 3), 'o') ylabel('exam 2 scores') xlabel('exam 1 scores') plot(x(:,2), (theta(1) - x(:,2)*theta(2))/theta(3), '-'); legend('admitted', 'unadmitted','decision boundary');
效果如图: