对于斐波拉契经典问题,我们都非常熟悉,通过递推公式F(n) = F(n - 1) + F(n - 2),我们可以在线性时间内求出第n项F(n),现在考虑斐波拉契的加强版,我们要求的项数n的范围为int范围内的非负整数,请设计一个高效算法,计算第n项F(n)。第一个斐波拉契数为F(0) = 1。给定一个非负整数,请返回斐波拉契数列的第n项,为了防止溢出,请将结果Mod 1000000007。
或者,现在有一栋高楼,但是电梯却出了故障,无奈的你只能走楼梯上楼,根据你的腿长,你一次能走1级或2级楼梯,已知你要走n级楼梯才能走到你的目的楼层,请计算你走到目的楼层的方案数,由于楼很高,所以n的范围为int范围内的正整数。
给定楼梯总数n,请返回方案数。为了防止溢出,请返回结果Mod 1000000007的值。
1.递归 时间复杂度O(2^n)
- int f(int n){
- if(n == 1 || n == 2){
- return 1;
- }
- return f(n-1) + f(n-2);
- }
2.循环 时间复杂度O(n)
- public int f(int n) {
- // write code here
- int f0 = 1;
- int f1 = 1;
- int f2 = 0;
- for(int i = 2; i < n; i++){
- f2 = f0 + f1;
- f0 = f1;
- f1 = f2;
- }
- return f2;
- }
3.矩阵求解 时间复杂度O(logn)
斐波那契的递推公式可以表示成如下矩阵形式:
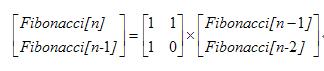
根据矩阵的分治算法,可以在O(logn)时间内算出结果。
public class Fibonacci {
static long[][] f = new long[][]{{0,1},{1,1}};
public int getNthNumber(int n) {
if(n == 0)
return 1;
if(n == 1)
return 1;
f = pow(n,f);
return (int) (f[1][1]%1000000007);
}
private long[][] pow(int n,long[][] f){//矩阵的幂函数
if(n == 1)
return f;
if(n == 2)
return fun(f,f);
if((n&1)==0){//偶数
f = pow(n/2,f);
return fun(f, f);
}
else
return fun(pow(n/2,f),pow(n/2 + 1,f));
}
private long[][] fun(long[][] f,long[][] m){
long[][] temp = new long[2][2];
temp[0][0] = (f[0][0]*m[0][0] + f[0][1]*m[1][0]);
temp[0][1] = (f[0][0]*m[0][1] + f[0][1]*m[1][1]);
temp[1][0] = (f[1][0]*m[0][0] + f[1][1]*m[1][0]);
temp[1][1] = (f[1][0]*m[0][1] + f[1][1]*m[1][1])%1000000007;
return temp;
}
}