#include<bits/stdc++.h> using namespace std; #define N 35 #define INF 1e9 int dis[N][N],n,len,ans; int main(){ while(scanf("%d",&n)){ if(!n) break; for(int i=1;i<=n;i++) for(int j=i+1;j<=n;j++) scanf("%d",&dis[i][j]),dis[j][i]=dis[i][j]; ans=dis[1][2]; for(int i=3;i<=n;i++){ len=INF; for(int j=1;j<=n;j++) for(int k=j+1;k<=n;k++) if(j!=i && k!=i) len=min(len,(dis[i][j]+dis[i][k]-dis[j][k])/2); ans+=len; } printf("%d ",ans); } return 0; }
一道构造题。666
锻炼思维的好题,需要运用一些树的性质。以下用g(i,j)表示点i与点j之间的距离。
首先,我们考虑n=2时的情况,很显然答案就是g(1,2)。
接下来考虑n=3时的情况。由于所有点均为叶子节点,很显然点3是从点1到点2的路径上分叉出来的,就像下图。
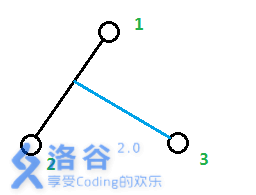
设蓝色部分长度为len,那么答案就是g(1,2)+len。len怎么求呢?显然,len = (g(1,3)+g(2,3)-g(1,2))/2。
n>3的情况也同理。枚举i,看看点n是不是从点1~i的路径上分叉出来的,求出的最小len就是要加到答案里面去的。如下图。
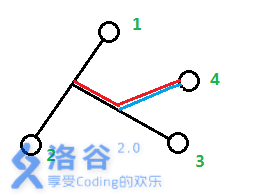
如果认为点4是从1~2的路径上分叉出来的,答案就会加上红色部分的长度。但是红色部分长度显然有一部分是多余的。只有认为点4是从1~3的路径上分叉出来的,才能加上正确答案(也就是蓝色部分)。