一、5436. 一维数组的动态和:
给你一个数组 nums 。数组「动态和」的计算公式为:runningSum[i] = sum(nums[0]…nums[i]) 。
请返回 nums 的动态和。
示例:
输入:nums = [1,2,3,4]
输出:[1,3,6,10]
解释:动态和计算过程为 [1, 1+2, 1+2+3, 1+2+3+4] 。输入:nums = [1,1,1,1,1]
输出:[1,2,3,4,5]
解释:动态和计算过程为 [1, 1+1, 1+1+1, 1+1+1+1, 1+1+1+1+1] 。
分析:
一遍遍历即可。
代码(Python):
class Solution:
def runningSum(self, nums: List[int]) -> List[int]:
pre = 0
ans = []
for val in nums:
pre += val
ans.append(pre)
return ans
二、5437. 不同整数的最少数目:
给你一个整数数组 arr 和一个整数 k 。现需要从数组中恰好移除 k 个元素,请找出移除后数组中不同整数的最少数目。
示例:
输入:arr = [5,5,4], k = 1
输出:1
解释:移除 1 个 4 ,数组中只剩下 5 一种整数。输入:arr = [4,3,1,1,3,3,2], k = 3
输出:2
解释:先移除 4、2 ,然后再移除两个 1 中的任意 1 个或者三个 3 中的任意 1 个,最后剩下 1 和 3 两种整数。
分析:
(1)首先需要对数组中元素进行计数,Python提供了基于哈希表实现的Counter。
(2)接着就是排序加遍历,个数少的数优先-1,当个数为0时去除。
代码(Python):
class Solution:
def findLeastNumOfUniqueInts(self, arr: List[int], k: int) -> int:
counter = Counter(arr)
res = []
for key in counter:
res.append([key, counter[key]])
res.sort(key=lambda x: -x[1])
while k > 0:
res[-1][1] -= 1
k -= 1
if res[-1][1] == 0:
res.pop()
return len(res)
三、5438. 制作 m 束花所需的最少天数:
给你一个整数数组 bloomDay,以及两个整数 m 和 k 。
现需要制作 m 束花。制作花束时,需要使用花园中 相邻的 k 朵花 。
花园中有 n 朵花,第 i 朵花会在 bloomDay[i] 时盛开,恰好 可以用于 一束 花中。
请你返回从花园中摘 m 束花需要等待的最少的天数。如果不能摘到 m 束花则返回 -1 。
示例:
输入:bloomDay = [1,10,3,10,2], m = 3, k = 1
输出:3
解释:让我们一起观察这三天的花开过程,x 表示花开,而 _ 表示花还未开。
现在需要制作 3 束花,每束只需要 1 朵。
1 天后:[x, _, _, _, _] // 只能制作 1 束花
2 天后:[x, _, _, _, x] // 只能制作 2 束花
3 天后:[x, _, x, _, x] // 可以制作 3 束花,答案为 3输入:bloomDay = [1,10,3,10,2], m = 3, k = 2
输出:-1
解释:要制作 3 束花,每束需要 2 朵花,也就是一共需要 6 朵花。而花园中只有 5 朵花,无法满足制作要求,返回 -1 。
分析:
(1)去重、排序:
由于题目给出的bloomDay数组中可能含有重复元素。并且题目需要我们返回最少的天数。因此提示我们还需要升序排序。因此我们可以先处理数据。
bloom_order = sorted(set(bloomDay))
(2)遍历:
如果直接使用 for day in bloom_order:来进行排序,会超时。由于超过最小天数的天数也能够满足制作m束花的需求。因此满足二分的性质:单调性。因此可以使用二分查找来优化。
(3)统计个数:
如果直接对每个位置都进行求取其后k个元素的值,会进行两层循环:
# O(N * k), 超时!!!
for i in range(len(bloomDay)):
for j in range(k):
# ...
还可以定义两个变量,分别保存可以制作的花的数量num,以及相邻k朵花中开放的花数量sums:
for i in range(len(bloomDay)):
if num >= m:
break
if bloomDay[i] <= day:
sum += 1
else:
sums = 0
if sums == k:
num += 1
sums = 0
return num >= m
代码(Python):
class Solution:
def minDays(self, bloomDay: List[int], m: int, k: int) -> int:
def check(day):
num = sums = 0
for i in range(len(bloomDay)):
if num >= m:
break
if bloomDay[i] <= day:
sums += 1
else:
sums = 0
if sums == k:
num += 1
sums = 0
return num >= m
length = len(bloomDay)
if length < m * k:
return -1
bloom_order = sorted(set(bloomDay))
left, right = 0, len(bloom_order) - 1
while left <= right:
mid = (left + right) // 2
if check(bloom_order[mid]):
right = mid - 1
else:
left = mid + 1
return bloom_order[left]
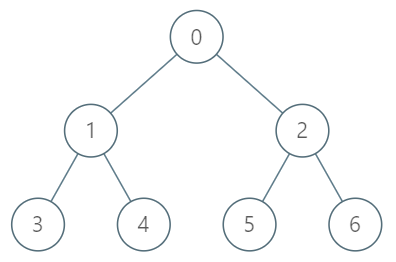
四、1483. 树节点的第 K 个祖先:
给你一棵树,树上有 n 个节点,按从 0 到 n-1 编号。树以父节点数组的形式给出,其中 parent[i] 是节点 i 的父节点。树的根节点是编号为 0 的节点。
请你设计并实现 getKthAncestor(int node, int k) 函数,函数返回节点 node 的第 k 个祖先节点。如果不存在这样的祖先节点,返回 -1 。
树节点的第 k 个祖先节点是从该节点到根节点路径上的第 k 个节点。
示例:
输入:
["TreeAncestor","getKthAncestor","getKthAncestor","getKthAncestor"]
[[7,[-1,0,0,1,1,2,2]],[3,1],[5,2],[6,3]]输出:
[null,1,0,-1]解释:
TreeAncestor treeAncestor = new TreeAncestor(7, [-1, 0, 0, 1, 1, 2, 2]);treeAncestor.getKthAncestor(3, 1); // 返回 1 ,它是 3 的父节点
treeAncestor.getKthAncestor(5, 2); // 返回 0 ,它是 5 的祖父节点
treeAncestor.getKthAncestor(6, 3); // 返回 -1 因为不存在满足要求的祖先节点
分析:
看了官方题解。提到一种ACM的模板题解法——Binary Lifting。这里贴一个题解。之后遇到类似的题再仔细分析一下。
代码(Python):
class TreeAncestor:
def __init__(self, n: int, parent: List[int]):
self.cols = 20 # log(50000) < 20
self.dp = [[-1] * self.cols for _ in range(n)]
for i in range(n):
self.dp[i][0] = parent[i]
for j in range(1, self.cols):
for i in range(n):
if self.dp[i][j - 1] != -1:
self.dp[i][j] = self.dp[self.dp[i][j - 1]][j - 1]
return
def getKthAncestor(self, node: int, k: int) -> int:
for i in range(self.cols - 1, -1, -1):
if k & (1 << i):
node = self.dp[node][i]
if node == -1:
break
return node
# Your TreeAncestor object will be instantiated and called as such:
# obj = TreeAncestor(n, parent)
# param_1 = obj.getKthAncestor(node,k)