预备知识:多项式除法
上一节我们讲了checksum

这一节我们来讲CRC
How do CRCs work
CRC: the cyclic redundancy check

从下面几个章节来讲,
首先是讲一下如何通过 模除运算 来检测错误,为了给你后面学习CRC提供一些sense

现在有hello world, o变成了n , r变成了s
checksum是不能检测出错误的,

两个 big long binary string 的等价十进制数字
我们用着两个数字除以 251

余是50和52, 通过求余运算,我们就能检测错误。。
================================================================================================================
下面,

hi! 是上面那一行,
我们想为这一行增加一些extra byte,
(fill these extra bytes in here with our check sequence)
首先我们加0, 最后16位都是0,生成了一个十进制的数字
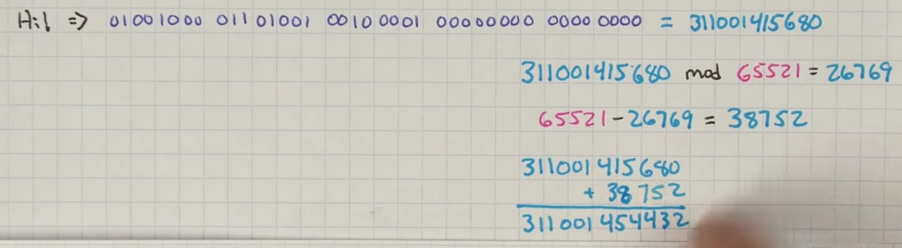
用这个数字模 65521 得到 26769
然后用65521 – 26769 = 38752
然后用这坨数字加上38752
这样得到的数,就能被65521整除
(
这是一个数学原理
例如,
5%3 = 2
3-2=1
5+1=6
)

我们把 38752 加到最后两个字节上

这个东西模65521的值就是0
所以,在校验中,如果我们得到的message 模 65521的值不是0,我们就知道了,一定是传输中出现错误了

(将hi! 改成ho!)
===============================================
现在我们在传输的数据中加入一些错误:

receive的message (r)= trans的message(t) + error message(e)
t可以被65521整除
r不可以被 65521整除,是因为e不可以被65521整除,
我们选了65521这个数字,,,没选256..(如果选256就不行了,所以这个算法中选数也是有一定要求的,这个算法中,选择的这个特定数字,决定可以容忍e错误位数多少,)
注意,e可以被256整除的,(anything where the last 8 bits are zeros is a multiple of 256)

在这个例子中(从Hi!变成Ho!), r被error改变了两位, 但是实际因为有进位问题,可能被e不只是两位, (下图是从Ho!变成Hi!)

如果这样的话,e和r之间的位数就不能统一了,在找那个合适的除数的时候,会造成一些困难,(因为我们特定除数只能对特定位数e有效,进位这样乱搞,e的位数不能保证)
======================================================================
所以,crc并没有把message当成特定number来传输, 而是使用多项式

在这个例子中r只有两个位变了,但是因为进位的影响,错误e中有很多位。
 72用二进制是这样子表示的,如果我们在72上+一个8,
72用二进制是这样子表示的,如果我们在72上+一个8,
我们并不是在1*2^3 那里变成 2*2^3
而是进位变成了1*2^4
为了避免进位的问题,
在CRC中,没有用2,而是用x(没有用number,以此来避免进位的问题)
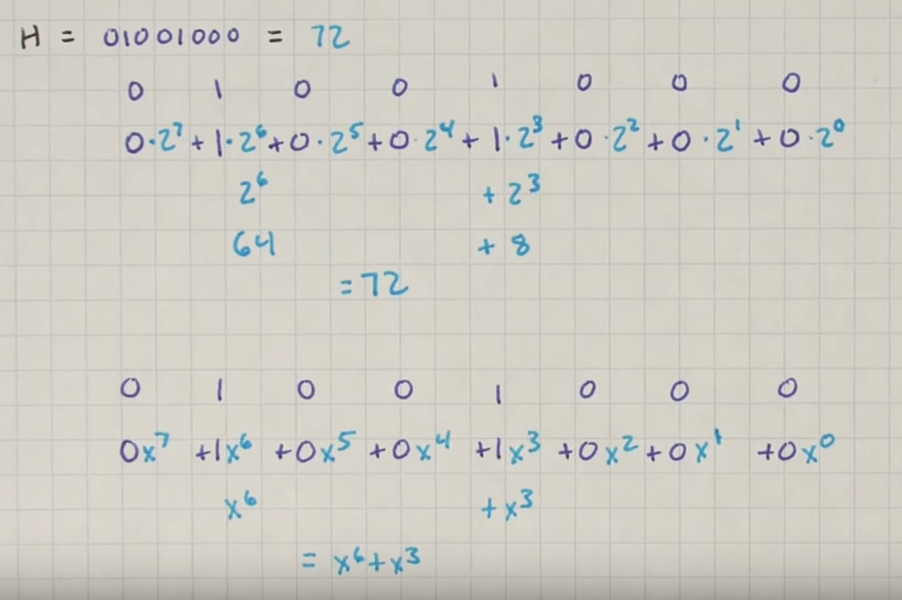
现在如果我们加8 ,结果就是2*x^3 在这一位上直接加,而不会碰到x^4这位
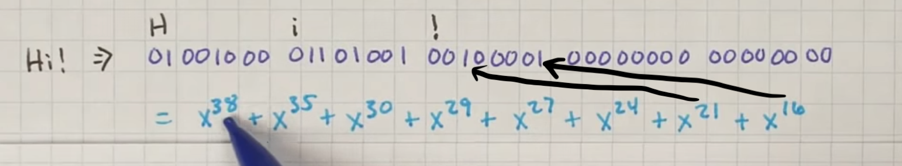
(不会被进位所影响)
然后我们用 下面这个多项式来除

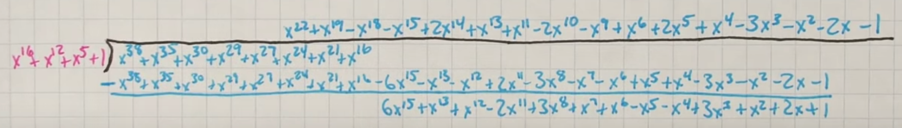
(和我们在文章一开始做的一样, 找了一个数..就去相除,得到结果)
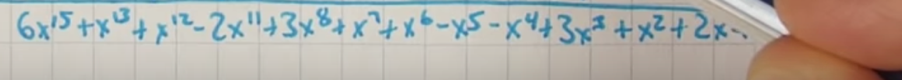
得到的这个结果如何转换为二进制, 比如说 6x^15,我们不能在一行二进制的第16位写6(6*2^15)。。。因为二进制里没有6, 下面介绍一个数学工具
===================================================================
finite fields 有限域
代数(algebra)
algebra is basically the set of rules that you can use to manipulate symbols
比如这个图片中,我们想算x,就是对他实行各种algebra rules

上图中对x的一个计算,应用了
additive property of equality
multiplicative property of equality
在algebra的计算中,你一直在使用numbers,
这些numbers组成了field
上面的计算中用的是real numbers field 实数域
还有很多域,比如复数域。。
Finite Fields(有限域)
a finite filed uses a finite number of numbers, but still all the rules of algebra work just the same.
什么是filed?
a filed is basically just a set of numbers and then definition of how you add those numbers together and how you multiply those numbers
field has to obey certain rules in order to be a valid field in order for algebra to still work.
Field axioms 域公理

结合律、交换律、分配律...
any set of numbers in any definition that you want to
of multiplication and addition
as long as it meets all these axioms then,
your rules will work all the rest of algebra
我们定义有限域[0,1],定义一些rules

定义有限域F=[0,1],满足Field axioms
虽然上面有些东西看上去不符合直觉,
比如
在Field axioms中 additive inverse : a+(-a) = 0 ,但这里1+1=0.
是因为在我们的F中,只是inverse是这个数本身,所以这一条也是满足的
回到刚才的算式中:

如果我们用有限域F,就能继续解决刚才的问题了,
===================================================
多项式相除

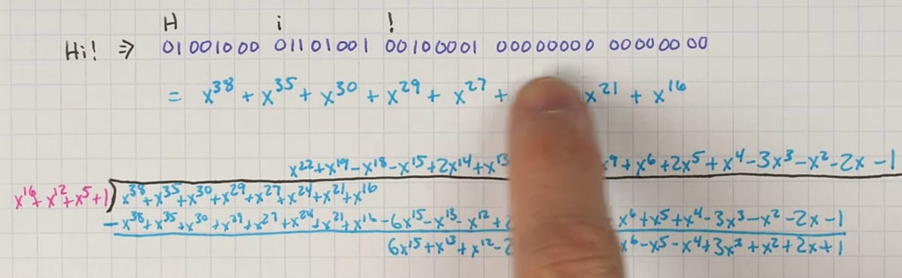
在这个表达式中,我们留了16位来fill我们的CRC,
我们的除数被称作 generator polynomial

进行除法,
在处理到x^22的时候, 0 – x^22 ,并不是 -x^22
我们要使用我们的有限域进行运算
在F中,0-1的值是1,所以0-x^22 结果是 x^22

在计算中,
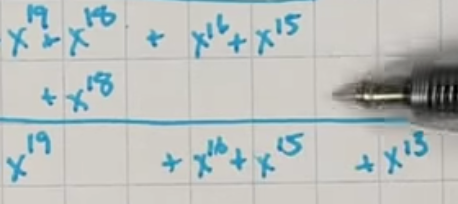
我们也应该注意到这很像xor门,因为上下都有的时候会变成0,有一个的时候会保留,

到最后算出余数
because we use the finite field when we did this whole division process what you’ll see is that all of our coefficients(系数) are either 0 or 1, right?
so we could actually convert this remainder now to a binary number
the finite field even though it’s kind of weird and we had to redefine some of the addition and multiplication,
A little bit algebra still works and that’s the whole that’s the whole reason to use it
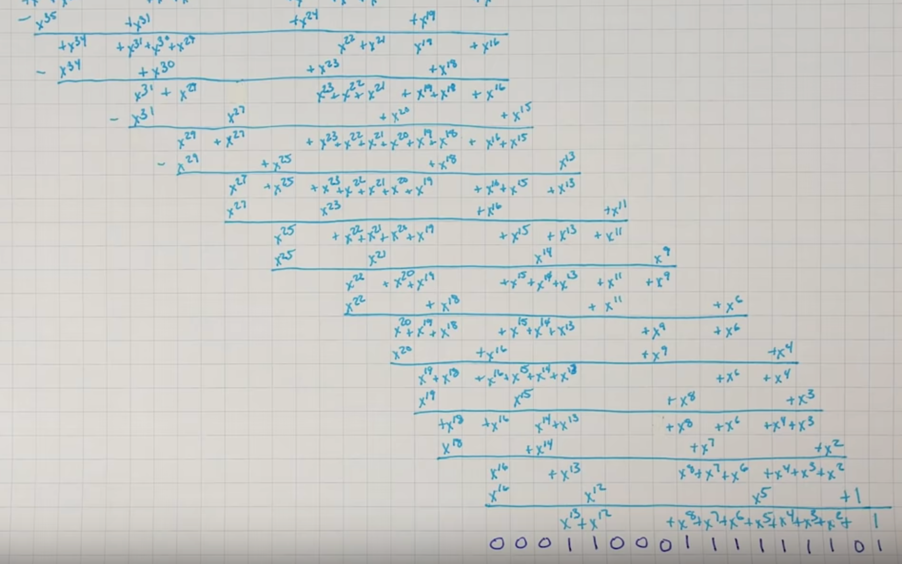


x^13 + x^12 + … … 从这一位开始是运算的结果——m(x) mod g(x) 的余数,
我们最后就可以把二进制数写出来了,是01001000 01101001 .....
下面加上校验位,
然后我们要在后面加16个位的校验 0000 0000 0000 0000
我们称x那一坨多项式为m(x)
t(x) = m(x) – (m(x) mod g(x)). 中间计算使用的是F(0,1)有限域的二进制计算
(
还是那个原理,
5%3 =2
5-2=3
3%3=0
)
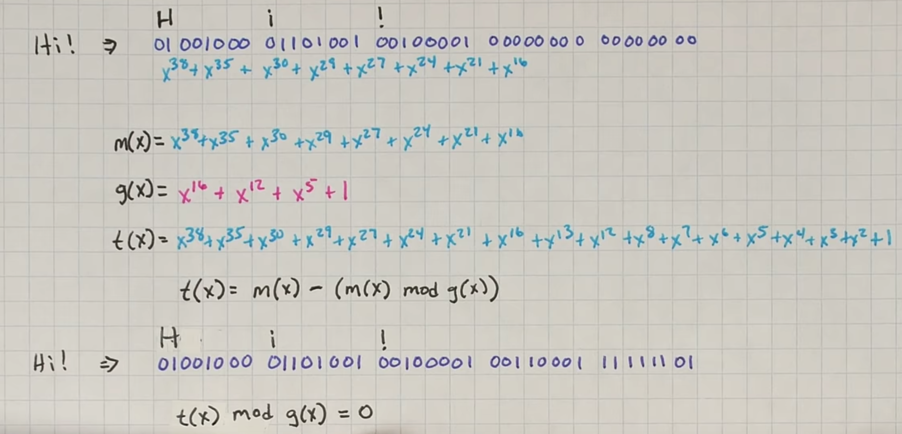
当receiver拿到t(x)后,用t(x) mod g(x) 得到的值是 0

如果求得余数不是0,那么说明是有错误的。

如果求得的余数不是0,那么说明是有错误的。
==========================================================================================================

generator polynomial是怎么来的

最后接收方要收到的是t(x) ,要求是t(x) mod g(x) = 0,
所以我们期望的是((tx) + e(x)) mod g(x) !=0
所以我们只要选取出e(x) mod g(x) 不为0的,就是合适的g(x)
Detecting single-bit errors:
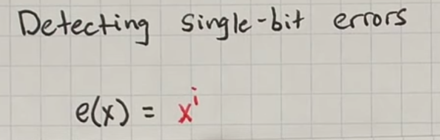
例如:
in order to detect this we need to come up with a polynomial that is not a multiple of X to the I (x^i),
为了检测出单比特错误,我们要找的g(x) 要求不是 x^i 的倍数
g(x):
with at least 2 terms (e.g. x+1)

Detecting two-bit errors:
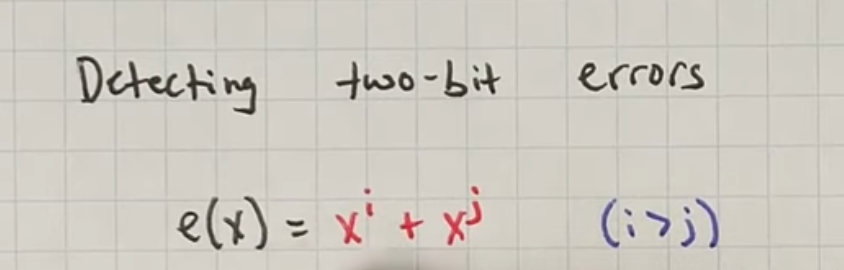
the goal is come up with a generator polynomial that is not a multiple of this expression
上式也可以写成

写成

(k is the distance between two errors)
我们直接给出一个g(x):

对应这个g(x), if your message less than 32k,then this particular polynomial will be able to detect any two-bit errors within that message, 这个可以在数学上严格证明
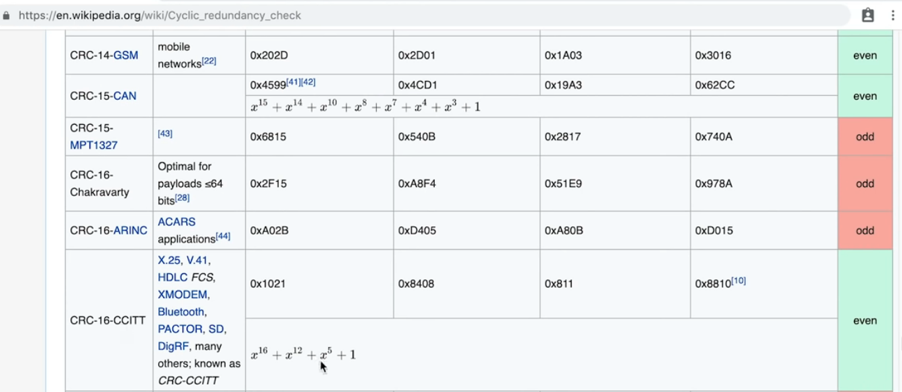
通过WIKI我们可以看到,我们给出的这个叫做CRC-16-CCITT (Bluetooth就用的这个..)
还有CRC32.。
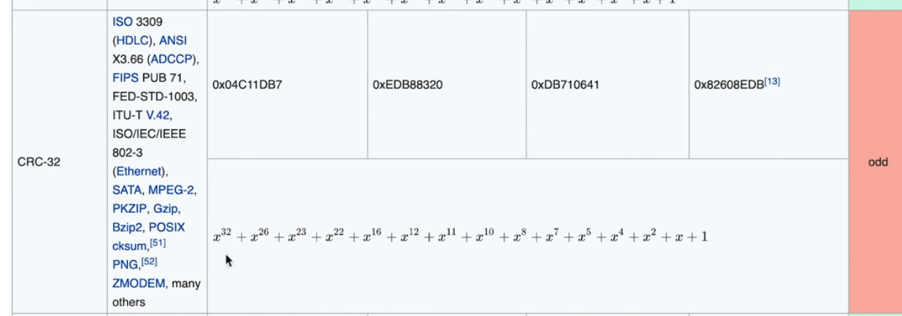
802-3(Ethernet) ----> wifi 就用的这个
PNG什么的
…
还有一些更好的CRC变种

看一下
Koopman(CRC-32K)教授的CRC
http://users.ece.cmu.edu/~koopman/crc/
看一下这张表中,对应HD=4折一行的16折一列对应的表格值的意思
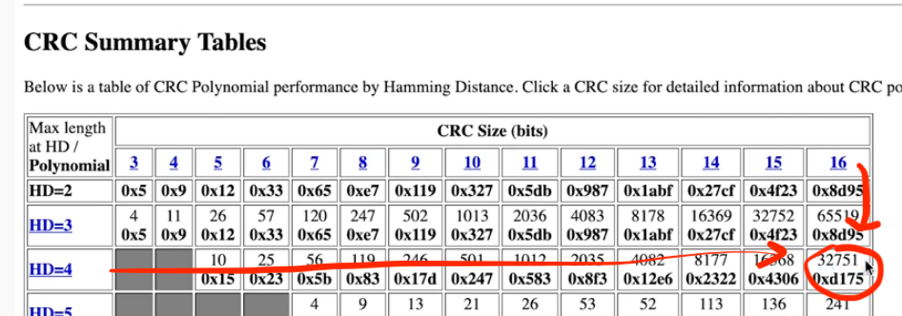
Max length of Hamming distance is the minimum number of bits that you’d have to change between two messages in order to not detect an error.
HD=4的意思是
in this case a Hamming distance of four
means that you can change any three bits in the message and guaranteed to detect it
这一行这一列对应的意思是:
this particular 16 bit CRC will give you that and it’ll give you that for messages up to 32K long
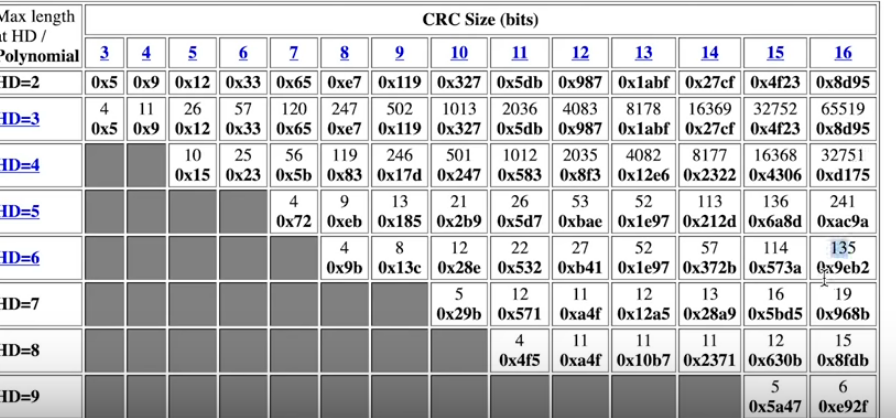
you can get higher hamming distances, but you see the message size gets smaller
Detecting burst errors:

k is the length of burst
x^i 是最右边的错误位,k是burst error的长度 ,所以x^i(x^k-1 + … + 1)

因为结果[t(x)] % g(x) = 0
所以我们期望((tx) + e(x)) mod g(x) !=0
我们要求ex除以gx 使余数不为0
假设g(x)最高项位数是16
e(x)的项数只要少于16,就不可能被整除..
所以
any 16-bit crc is always going to protect against at least 16-bit burst errors
a 32-bit crc is always going to protect against at least 32-bit burst errors and so forth