二叉查找树 Binary Search Tree
二叉查找树的定义
二叉查找树又称二叉搜索树。其要求在二叉树中的任意一个节点,其左子树中的每个节点的值,都要小于这个节点的值,而右子树的节点的值都大于这个节点的值。
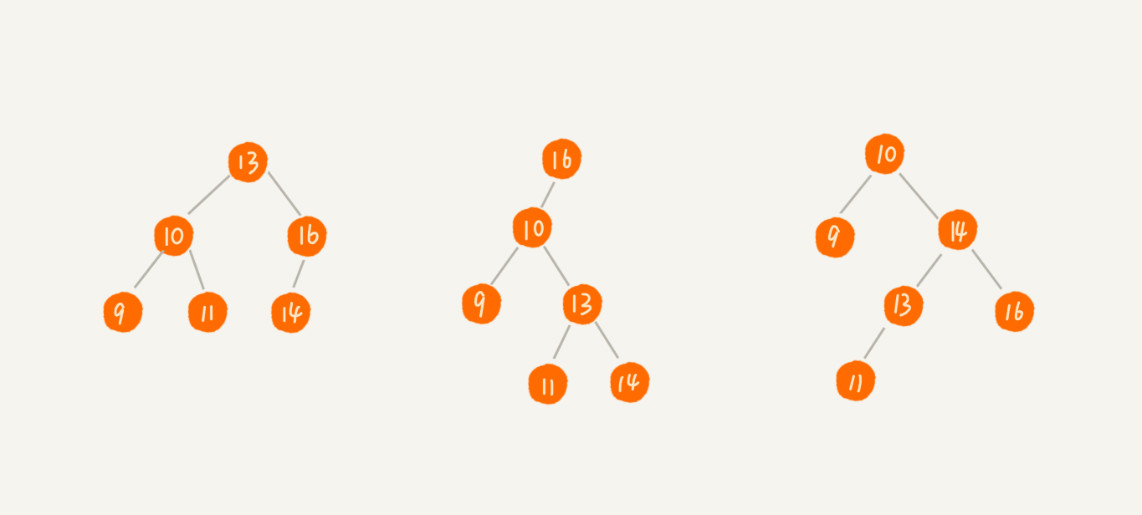
二叉查找树的查找操作
二叉树类、节点类以及查找方法的代码实现
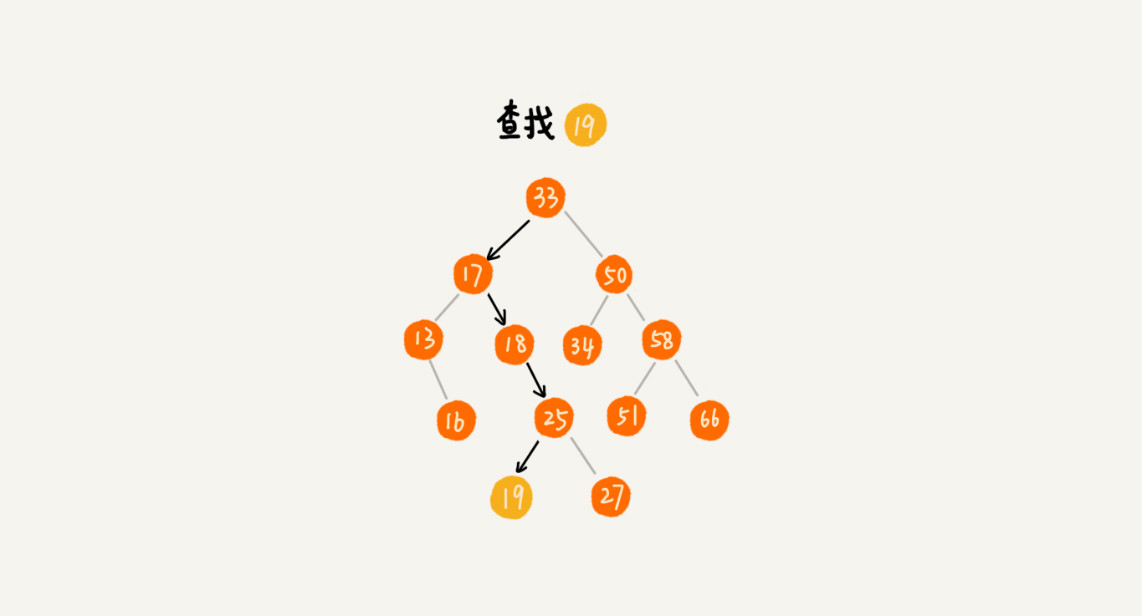
先取根节点,如果它等于我们要查找的数据,那就返回。
如果要查找的数据比根节点的值小,那就在左子树中递归查找;
如果要查找的数据比根节点的值大,那就在右子树中递归查找。
public class BinarySearchTree{ //二叉树节点类 public class Node{ //自动属性:整型数据,左节点、右节点引用域 public int Data { get; set; } public Node Left { get; set; } public Node Right { get; set; } public Node(int data){ Data = data; } } //根结点 private Node tree; public Node Tree{get{return tree;}} //查找方法 public Node Find(int data){ //从根节点遍历 Node p = tree; while (p != null){ if (data > p.Data) p = p.Right; else if (data < p.Data) p = p.Left; else return p; } return null; } }
二叉查找树的插入操作
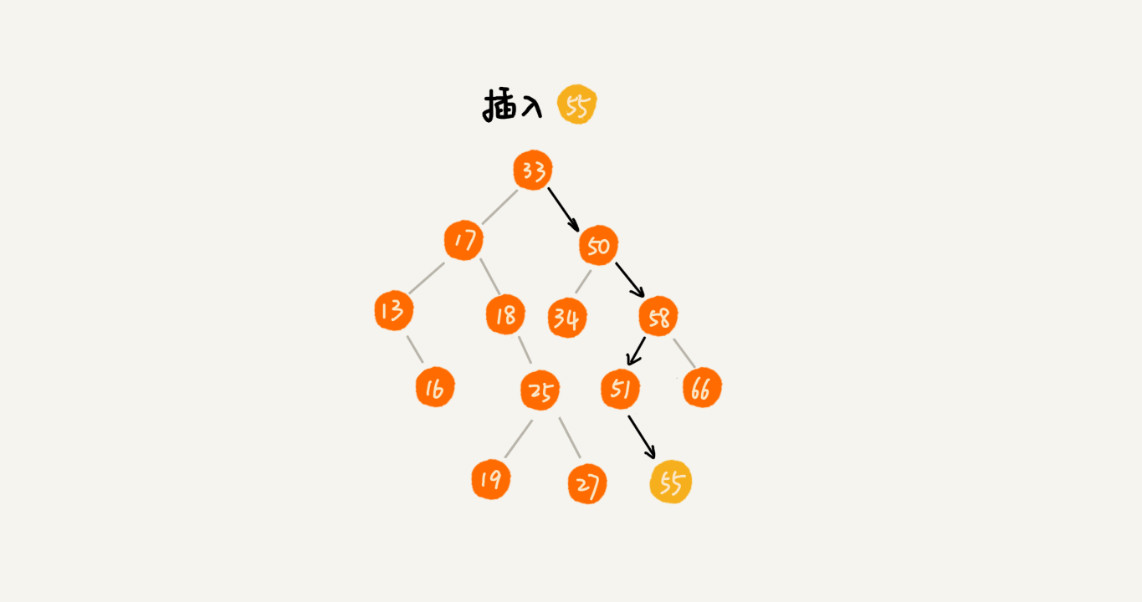
新插入的数据一般都是在叶子节点上,所以我们只需要从根节点开始,依次比较要插入的数据和节点的大小关系。
如果要插入的数据比节点的数据大,并且节点的右子树为空,就将新数据直接插到右子节点的位置;如果不为空,就再递归遍历右子树,查找插入位置。
同理,如果要插入的数据比节点数值小,并且节点的左子树为空,就将新数据插入到左子节点的位置;如果不为空,就再递归遍历左子树,查找插入位置。
public void Insert(int data){ //没有根节点则插入根节点 if (tree == null) { tree = new Node(data); return; } //遍历根节点 Node p = tree; while (p!=null){ //根据数据大小找到左右子树对应的叶节点,将数据插入 if (data >= p.Data){ if (p.Right == null){ p.Right = new Node(data); return; } p = p.Right; } else if (data < p.Data){ if (p.Left == null){ p.Left = new Node(data); return; } p = p.Left; } } }
二叉查找树的删除操作
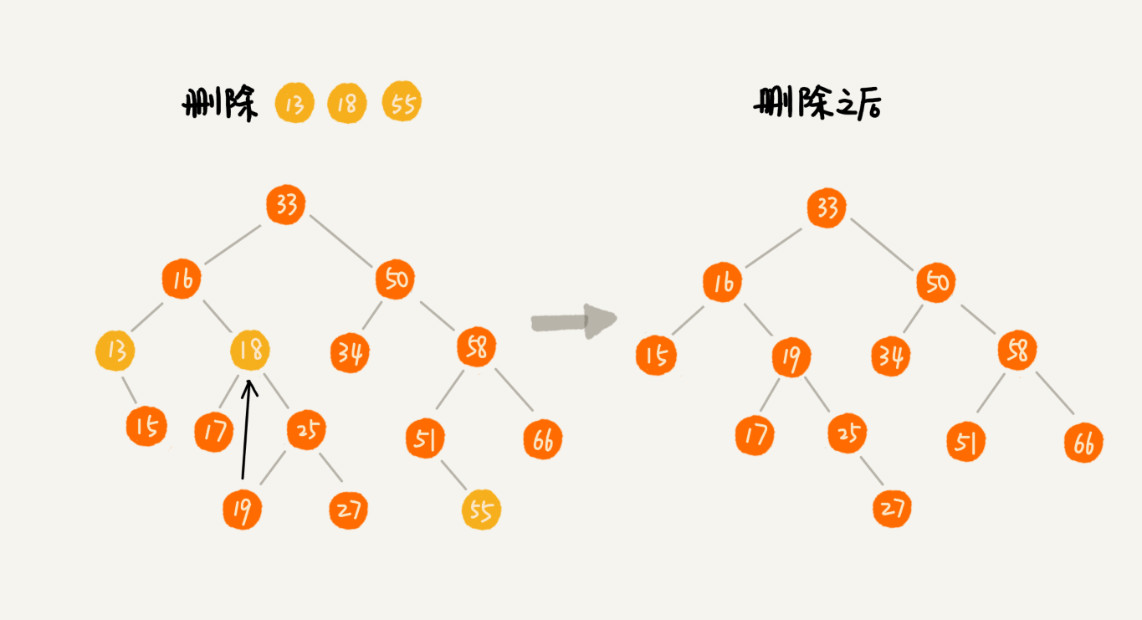
第一种情况,删除的节点没有子节点直接将其父节点指向置为null。
第二种情况,删除的节点只有一个子节点,将其父节点指向其子节点。
第三种情况,删除的节点有两个子节点,首先找到该节点右子树中最小的的节点把他替换掉要删除的节点 然后再删除这个最小的节点,该节点必定没有子节点,否则就不是最小的节点了
public void Delete(int data){ Node p = tree;//p指向要删除的节点 Node pp = null;//记录p的父节点 while (p != null && p.Data != data){ pp = p; if (data > p.Data) p = p.Right; else p = p.Left; } if (p == null) return; //要删除的节点有两个子节点 if (p.Left != null && p.Right != null){ Node minP = p.Right; Node minPP = p; while (minP.Left != null){ minPP = minP; minP = minP.Left; } p.Data = minP.Data; p = minP;//p节点的值更新为最小节点的值,使p指向最小节点,下面就变成了删除p pp = minPP; } //要删除的节点有一个子节点,就获取它的子节点 Node child; if (p.Left != null) child = p.Left; else if (p.Right != null) child = p.Right; 或者没有节点,子节点设为null else child = null; //要删除的节点是根节点 if (pp == null) tree = child; //删去节点,其父节点直接指向其子节点 else if (pp.Left == p) pp.Left = child; else pp.Right = child; }
关于二叉查找树的删除操作,还有个非常简单、取巧的方法,就是单纯将要删除的节点标记为“已删除”,但是并不真正从树中将这个节点去掉。
这样原本删除的节点还需要存储在内存中,比较浪费内存空间,但是删除操作就变得简单了很多。而且,这种处理方法也并没有增加插入、查找操作代码实现的难度。
二叉查找树的其他操作
二叉查找树中还可以支持快速地查找最大节点和最小节点、前驱节点和后继节点。
二叉查找树除了支持上面几个操作之外,还有一个重要的特性,就是中序遍历二叉查找树,可以输出有序的数据序列,时间复杂度是 O(n),非常高效。因此,二叉查找树也叫作二叉排序树。
下面使用一组测试数据,其数据结构如下所示
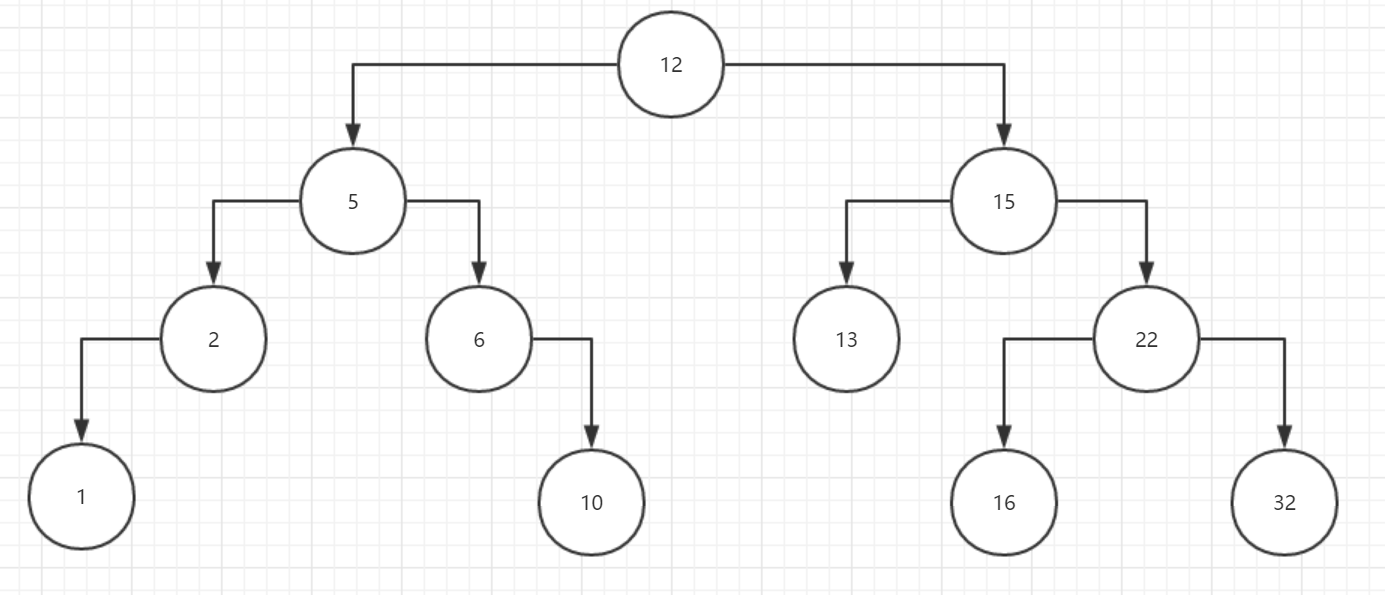
测试数据Program类
class Program{ static void Main(string[] args){ BinarySearchTree b = new BinarySearchTree(); //插入数据 b.Insert(12); b.Insert(15); b.Insert(5); b.Insert(6); b.Insert(2); b.Insert(22); b.Insert(32); b.Insert(10); b.Insert(16); b.Insert(13); b.Insert(1); //层序遍历 b.LevelOrder(); Console.WriteLine(); //删除节点 b.Delete(15); //再层序遍历 b.LevelOrder(); Console.WriteLine(); //中序遍历 b.InOrder(b.Tree); Console.WriteLine("Over"); Console.ReadKey(); } }
层序遍历和中序遍历二叉查找树
//层序遍历,广度优先搜索 public void LevelOrder(){ Queue<Node> q = new Queue<Node>(); //根节点入栈,循环遍历栈,直到栈空 q.Enqueue(tree); while (q.Count != 0){ //打印出栈的数据 Node node = q.Dequeue(); Console.Write(node.Data + ","); //将出栈的节点的子节点入栈 if (node.Left != null) q.Enqueue(node.Left); if (node.Right != null) q.Enqueue(node.Right); } } //中序遍历,相当于排序 public void InOrder(Node node){ if (node == null) return; InOrder(node.Left); Console.Write(node.Data + ","); InOrder(node.Right); }
输出结果
12,5,15,2,6,13,22,1,10,16,32, 12,5,16,2,6,13,22,1,10,32, 1,2,5,6,10,12,13,16,22,32,Over
支持重复数据的二叉查找树
前面的二叉查找树的操作,我们默认树中节点存储的都是数字,针对的都是不存在键值相同的情况。
我们可以通过两种办法来构建支持重复数据的二叉查找树。
第一种方法
二叉查找树中每一个节点不仅会存储一个数据,因此我们通过链表和支持动态扩容的数组等数据结构,把值相同的数据都存储在同一个节点上。
第二种方法
每个节点仍然只存储一个数据。在查找插入位置的过程中,如果碰到一个节点的值,与要插入数据的值相同,我们就将这个要插入的数据放到这个节点的右子树,也就是说,把这个新插入的数据当作大于这个节点的值来处理。
当要查找数据的时候,遇到值相同的节点,我们并不停止查找操作,而是继续在右子树中查找,直到遇到叶子节点,才停止。这样就可以把键值等于要查找值的所有节点都找出来。
对于删除操作,我们也需要先查找到每个要删除的节点,然后再按前面讲的删除操作的方法,依次删除。
二叉查找树的时间复杂度分析
最坏、最好情况
如果根节点的左右子树极度不平衡,已经退化成了链表,所以查找的时间复杂度就变成了 O(n)。
最理想的情况,二叉查找树是一棵完全二叉树(或满二叉树)。不管操作是插入、删除还是查找,时间复杂度其实都跟树的高度成正比,也就是 O(height)。而完全二叉树的高度小于等于 log2n。
平衡二叉查找树
我们需要构建一种不管怎么删除、插入数据,在任何时候都能保持任意节点左右子树都比较平衡的二叉查找树,这就是一种特殊的二叉查找树,平衡二叉查找树。
平衡二叉查找树的高度接近 logn,所以插入、删除、查找操作的时间复杂度也比较稳定,是O(logn)。
二叉查找树相比散列表的优势
散列表中的数据是无序存储的
如果要输出有序的数据,需要先进行排序。而对于二叉查找树来说,我们只需要中序遍历就可以在 O(n) 的时间复杂度内,输出有序的数据序列。
散列表扩容耗时很多
而且当遇到散列冲突时,性能不稳定,尽管二叉查找树的性能不稳定,但是在工程中,我们最常用的平衡二叉查找树的性能非常稳定,时间复杂度稳定在 O(logn)。
散列表存在哈希冲突
尽管散列表的查找等操作的时间复杂度是常量级的,但因为哈希冲突的存在,这个常量不一定比 logn 小,所以实际的查找速度可能不一定比 O(logn) 快。
加上哈希函数的耗时,也不一定就比平衡二叉查找树的效率高。
散列表装载因子不能太大
为了避免过多的散列冲突,散列表装载因子不能太大,特别是基于开放寻址法解决冲突的散列表,不然会浪费一定的存储空间。
综合这几点,平衡二叉查找树在某些方面还是优于散列表的,所以,这两者的存在并不冲突。
思考
如何通过编程,求出一棵给定二叉树的确切高度呢?