上一节我们提到了如何在一张画布上画一个简单几何图形,通过创建画布,获取WebGLRendering上下文,创建一个简单的着色器,然后将一些顶点数据绑定到gl的Buffer中,最后通过绑定buffer数据,提供buffer中顶点数据的情况,执行渲染绘制方法,将数据结果从buffer中刷新到帧缓存中。整个流程十分清晰明了,可是通过对比原来OpenGL中的整个流程,我们会发现其中还缺少了一些很重要的处理步骤,虽然我们创建了属于自己的着色器,可并没有对顶点数据进行类似于顶点处理管线中的模型视图变换、透视投影变换等操作,仅仅只是在屏幕上实现了一个静态的几何图形。所以这一篇就让我们通过重新构造一个能够替代顶点处理管线的着色器,并利用该着色器对我们的几何图形进行相应的变换。
一 着色器中的变量
在上一节中提到了GLSL的着色器中有四种变量:顶点属性attribute/一致变量uniform/易变变量varying/常量const
- Uniform 全局变量,可以出现在顶点着色器、片元着色器中。一般对于所有顶点来说,可以共用共享的属性就可以用这种类型的变量定义。
- Attribute 顶点着色器专用的属性,从外部【一般从JavaScript中动态地获取】接收输入数据,主要用来表示逐顶点的信息。通常在GLSL中内置了一下关于顶点属性:
attribute vec4 gl_Color //顶点颜色
attribute vec4 gl_SecondaryColor //辅助顶点颜色
attribute vec3 gl_Normal //顶点法线
attribute vec4 gl_Position //顶点物体空间坐标
- Varying 如上一篇提到的,varying作为一个信使,将顶点着色器中的参数传递到片元着色器中,值得一提的是,Varying变量的数据类型只能被限制在: float、vec2、vec3、vec4、mat2、mat3以及mat4。其原因是因为,一般从顶点着色器传递过来的顶点数据往往会经过光栅器后再传递给片元着色器。在光栅化过程中,各个像素的值往往是根据顶点像素值进行内插的,如果顶点值是一些文本字符型的数据类型,则无法完成内插。
- Const常量,必须是常量,设定后不可修改。
二 仿射变换与矩阵
众所周知,屏幕是由一个个像素格组成,而我们在屏幕上画出来的几何图形也是由像素组成的。我们可以把几何图形变换的问题转换成为对像素图形变换的问题,也就是说,对几何图形中的所有像素进行操作,即可完成几何图形变换。
那么如何对像素进行几何图形变换呢?一般来说,我们会把屏幕看成一个坐标系统,屏幕上的几何图形处于这个坐标系统内,每个像素可视为屏幕坐标系中的一个点。这样一来,我们处理像素的问题,又转换成了处理坐标系中点位置的问题,从图形à像素à点,我们不断地分解抽象一个复杂的问题,并最终将其转换成为了方便求解的情景,这是我们处理问题的一个基本思路。
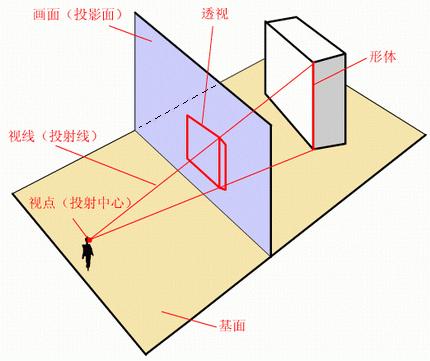

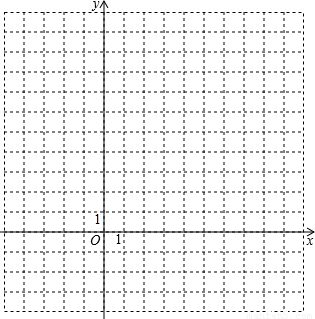
现实世界到数学世界的映射
既然把问题转移到了坐标系里,我们就可以将以前学到过的数学来求解这个问题。我们以二维坐标系为例,我们需要将一个点A(x , y)平移(a , b)到另一点A’,很简单,A’的坐标为(x+a, y+b),同理,将组成一个几何图形的若干个点全部进行平移操作,则这个几何图形也就完成一次平移。那如果我想对一个图形进行旋转呢?放大缩小呢?这些变换的操作仿佛没有平移那么直观,那么我们需要借助一些外力来解决这些问题。
齐次坐标:此处需要引入在OpenGL基础里提到过的齐次坐标,增加坐标的维度,这样可以让我们更方便的在低维空间中表示高维度的要素。这里有一个关于齐次坐标很好的解释:http://blog.csdn.net/janestar/article/details/44244849,这篇博客用齐次坐标证明了在平面空间里出现灭点的原因,很有趣。所以在一个平面直角坐标系中,我们可以用齐次坐标(x, y, 1)来表示一个点,这样一来,我们突然发现好像通过矩阵的点乘就可以到达实现点的绕轴旋转以及缩放图形的想法了!
我们希望能够用齐次坐标(x, y, 1)代表一个点,然后用每一个点的齐次坐标乘上一个3*3的变换矩阵,从而得到一个变换后的齐次坐标(x’, y’, 1),此时的x’和y’就是处理后的坐标,这是处理坐标仿射变换的一个基本思路。
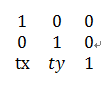
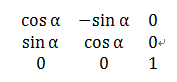

平移矩阵PY 旋转矩阵XZ 缩放矩阵SF
通过点(x, y, 1)·变换矩阵PY/XZ/SF可得到:
( x+tx, y+ty, 1) ( x·cosα + y·sinα,y·cosα - x·sinα )① ( x·sx, y·sy, 1)
① 关于旋转的数学证明,可参照以下证明:(主要通过三角函数的和差公式在单位圆中的关系进行证明)
假设平面直角坐标系O中,有一个半径为r的单位圆,点A为圆上一点(x, y),OA连线与X轴所成夹角为α,先将OA绕原点O逆时针旋转β°,求A点旋转至B点后的坐标值:
∵|OA| = x / cos α = y / sinα; |OB| = x' / cos(α+β) = y' / sin(α+β)
r = |OA| =|OB|
∴ x' = cos(α+β)·r,y' = sin(α+β)·r
通过三角函数的和差公式可得:
x' = r·(cosα·cosβ - sinα·sinβ) = x·cosβ - y·sinβ
y' = r·(sinα·cosβ + sinβ·cosα) = y·cosβ + x·sinβ
注意此处为逆时针旋转,β值小于0,所以此处得到的结果与上述公式有符号上的差异
三 连续变换
通过上述简单的介绍,已经大概能够了解到如何在平面直角坐标系中的几何图形进行仿射变换,但在现实操作中,我们往往会对一个图形进行多种变换操作,那该如何实现呢?
很简单,我们可以通过假设存在一个综合变换矩阵Z = F( PY·XZ·SF ),显而易见的是通过( x, y ,1 )·Z可以得到将点:1)先x, y缩放sx, sy倍;2)再旋转α弧度;3)最后x, y分别平移tx, ty个单位。不知你们发现没有,这儿有一个有趣的现象,我们明明是按照平移PY,旋转XZ以及缩放SF的顺序来作为行矩阵相乘的输入,可是在后面的过程文字说明中,我是按照逆向进行解释的。这是为什么呢?因为矩阵采用的是一个二维数组进行存储,而webGL在向着色器传入矩阵的过程中,是按列传入着色器的,即着色器按每列的数据进行处理。
一般来说,两个矩阵相乘,可以用如下方法表示:
multiply: function(a, b) { var a00 = a[0 * 3 + 0]; var a01 = a[0 * 3 + 1]; var a02 = a[0 * 3 + 2]; var a10 = a[1 * 3 + 0]; var a11 = a[1 * 3 + 1]; var a12 = a[1 * 3 + 2]; var a20 = a[2 * 3 + 0]; var a21 = a[2 * 3 + 1]; var a22 = a[2 * 3 + 2]; var b00 = b[0 * 3 + 0]; var b01 = b[0 * 3 + 1]; var b02 = b[0 * 3 + 2]; var b10 = b[1 * 3 + 0]; var b11 = b[1 * 3 + 1]; var b12 = b[1 * 3 + 2]; var b20 = b[2 * 3 + 0]; var b21 = b[2 * 3 + 1]; var b22 = b[2 * 3 + 2]; return [ b00 * a00 + b01 * a10 + b02 * a20, b00 * a01 + b01 * a11 + b02 * a21, b00 * a02 + b01 * a12 + b02 * a22, b10 * a00 + b11 * a10 + b12 * a20, b10 * a01 + b11 * a11 + b12 * a21, b10 * a02 + b11 * a12 + b12 * a22, b20 * a00 + b21 * a10 + b22 * a20, b20 * a01 + b21 * a11 + b22 * a21, b20 * a02 + b21 * a12 + b22 * a22, ]; }
通过上述代码可以发现:输入参数为a, b,但最终相乘是以b · a来实现的。在一般常见的WebGL API中,都是如此设计的:虽然从调用API的过程来看,输入顺序为:平移、旋转、缩放,可在API的具体实现中,则是按照缩放、旋转、平移的顺序来进行代码实现的。说实话,其实我也没太弄明白为什么要这样做,总感觉设计的比较反人类;有的资料建议可以从空间变换的角度来考虑这个问题,大意是:可以把操作对象假想成为空间而非空间中的几何体,随后的平移、旋转、缩放可以视为对空间所进行的操作,空间中的几何体不变的前提下,空间发生变换,几何体的位置坐标也就被动地发生了变化(因为几何体的位置完全依赖于空间坐标系提供的坐标值表达,失去了坐标系,几何体的位置信息就丢失了)。具体可见:https://webglfundamentals.org/webgl/lessons/zh_cn/webgl-2d-matrices.html;
<!-- 2D vertex shader --> <!-- attribute:同理由应用程序提供,一眼用于顶点着色器中 --> <!-- uniform:全局变量,由外部传递到着色器,只能读,不能修改 --> <!-- varying:易变变量,作为顶点着色器和片元着色器之间的通信 --> <script id="2d-vertex-shader" type="x-shader/x-vertex"> attribute vec2 a_position; uniform vec2 u_resolution; //矩阵 uniform mat3 u_matrix; void main() { // 2D-Vertex-shader: gl_Position = vec4((u_matrix * vec3(a_position, 1)).xy, 0, 1); } function draw(){ .....
//操作顺序:缩放、旋转、平移: //translationMatrix:平移矩阵; //rotationMatrix:旋转矩阵; //scaleMatrix:缩放矩阵 var matrix = m3.multiply(projectionMatrix, translationMatrix); matrix = m3.multiply(matrix, rotationMatrix); matrix = m3.multiply(matrix, scaleMatrix);
gl.uniformMatrix4fv(matrixLocation, false, matrix);
//Draw
gl.enable(gl.DEPTH_TEST);
gl.enable(gl.CULL_FACE);
//发出绘制命令
var primitiveType = gl.TRIANGLES;
var offset = 0;
var count = 16*6;
gl.drawArrays(primitiveType, offset, count);
}
PS:不同的变换顺序,如:平移--旋转--缩放和缩放--旋转--平移,这两个操作过程会得到完全不一样的两种效果,如果先平移再缩放的话,平移的距离会因为缩放的关系而发生伸长或缩短,完全背离了操作者的原本意图。在一般变换过程中,往往建议先缩放再平移。
本篇主要简述了再WebGL中,平面直角坐标系的几何图形仿射变换与矩形计算的关联实现,下一步会继续拓展到三维坐标系中,并增加相机、投影以及纹理等内容。
推荐一个很完整的入门教程:https://webglfundamentals.org/webgl/lessons/zh_cn/webgl-fundamentals.html,这是到目前为止,我参照最多的一个资料,特别是学习思路上。