Kruscal algorithm

#include <iostream>
#include <algorithm>
using namespace std;
#define MAX 5
#define INF 32765

int graph[MAX][MAX]=
{{INF ,1,INF,4,3},
{1,INF,2,INF,INF},
{INF,1,INF,2,3},
{4,INF,2,INF,1},
{3,INF,3,1,INF}};
typedef struct 
{ 
    int begin,end,length;
}Edge;
bool cmp(const Edge &edge1,const Edge &edge2)
{
    return edge1.length<edge2.length;
}
int origin(int path[],int v)//方法1：不带递归实现
{
    while(path[v]!=v)
        v=path[v];
    return v;
}
int originRecursive(int path[],int v)//方法2：递归实现
{
    if(path[v]==v)
        return v;
    return originRecursive(path,path[v]);
}
void main()
{   
    int i, j,k=0;
    Edge g[100],gb[100];
    int path[MAX]={0,1,2,3,4};
    int max=0;
    for(i=0;i<MAX;i++)
        for(j=i+1;j<MAX;j++ )
        {
            if(graph[i][j]<INF)
            {
                g[max].begin=i;g[max].end=j;
                g[max].length=graph[i][j];
                max++;
            }
        }
        for(i=0;i<max;i++)
            cout<<"["<<g[i].begin<<",  "<<g[i].end<<"]  "<<g[i].length<<endl;
        sort(g,g+max,cmp);
        for(i=0;i<max;i++)
            cout<<"[  "<<g[i].begin<<",  "<<g[i].end<<"]  "<<g[i].length<<endl;
        for(i=0;i<max;i++)
        {  
            int m,n;
            m=originRecursive(path,g[i].begin);
            n=originRecursive(path,g[i].end);
            if(m!=n)
            {
                m<n?path[n]=m:path[m]=n;
                gb[k++]=g[i];
            }
        }
        for(i=0;i<k;i++)
            cout<<"["<<gb[i].begin<<",  "<<gb[i].end<<"]  "<<gb[i].length<<endl;
}

originRecursive(path[],v)函数，是从v出发一直找到它的“祖先”的方法。
为了避免产生回路，故让path[大]=小，即  m<n?path[n]=m:path[m]=n;
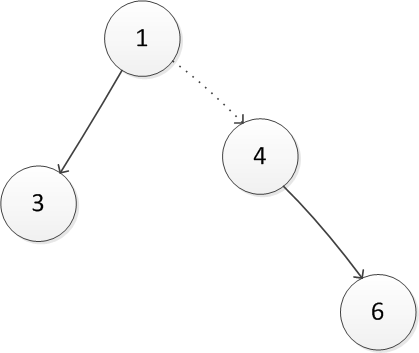
比如考虑（3，6）这条边，3的祖先是1，6的祖先是4，现在让这两个连通分量合并为1个连通分量，则让3，6的祖先产生关系，
如果不这样的话，直接让3，6产生关系，则4与6间的关系则没有了。