
一,基本的概念
节点:就是图中的1,2,3,4,5,6,7,8
节点的度:一个节点的孩子节点数。例,节点1的度为2,节点3的度为1,节点,7的度为0
树的度:他的节点的度数最高的度数。例,上图中,节点度数为2,则树的度为2.
叶子节点:没有孩子节点的节点。例如上图的4,5,7,8
分支节点:有孩子节点的节点。例,1,2,3,6
内部节点:非叶子节点,非根节点。例,2,3,6
父节点,子节点,这两个概念是相对的。
兄弟节点:同一个父节点,也包括堂兄对节点,例如,4,5,6
层次:上图中表示的层数。
二,特殊的二叉树
1,满二叉树:没有缺失的部分,他的节点的度为0/2
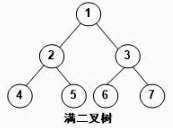
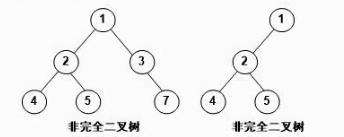
2,完全二叉树:除了最下面一层,上面的层都是满的树,最下面一层的节点是从左到右排列的。

3,非完全二叉树:不符合完全二叉树的条件的树
三,二叉树的特性

四,二叉树的遍历
二叉树遍历有多种方法:前序遍历,中序遍历,后序遍历,层次遍历
(1)层次遍历:遍历第一层,第二层,。。。第n层(每一层都是从左到右)

层次遍历的结果:1,2,3,4,5,6,7,8,
(2)前序
前序遍历顺序:根节点,左子节点,右子节点
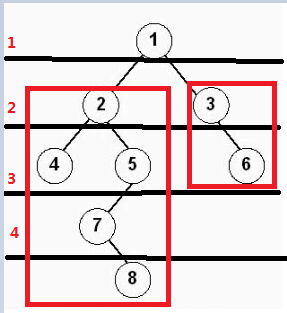
左边大框为左子树,右面大框为右子树,前序遍历,会先遍历根节点,在左子树,在右子树
先遍历1节点
在遍历左子树
在左子树中
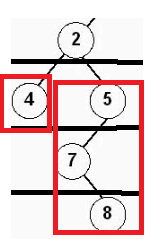
先遍历根节点2节点,在遍历左边部分4节点,在遍历右边节点,5,7,8
在遍历根节点的右节点

遍历顺序:根节点(3),右子节点(6)
综上前序:12457836
(3)中序
中序遍历顺序:左子节点,根节点,,右子节点


与前序类似
综上前序:42785136
(4)后序
后序遍历顺序:左子节点,右子节点,根节点,


与前序类似
综上前序:48752631
5,树转二叉树
(1)规则
孩子节点---->左子树节点
兄弟节点----->右孩子节点
(2)实例讲解

从跟节点开始,根节点有三个孩子节点,将作为二叉树的左子树节点
在三个孩子节点中将最左边的节点作为子节点,另外两个则是兄弟节点,
按照规则,兄弟节点将作为有右子节点,所以3,4作为2的右孩子节点,由于右
孩子节点只能有一个,将左边的3作为2 的右子节点,4作为3的兄弟节点,
同理转换为3 的右子节点。
在看3的子节点,有三个,同1 的三个子节点一样,5作为3 的左子树节点,
6作为5的右子树节点,7作为6的左子树节点。
在看4节点,经8,9作为左子树节点,选去左边的8作为左子树节点,
9作为8 的兄弟节点,转化为8的右子树节点。
结果如图所示

6,查找二叉树(排序二叉树)
查找二叉树是一类特殊的二叉树
特点:
(1)根节点的左子树节点都比根节点小
(1)根节点的右子树节点都比根节点大
意义:
他能极大地提高查询的速率
举例说明:
查找值为56的节点
(1)传统的方法:用每一个元素与56 相比,知道找到56为止
(2)查找二叉树:先用根节点与56相比,比56大,就在左子树中继续找,比56小就在右子树中找,大大提高了效率


7,最优二叉树(哈夫曼树)

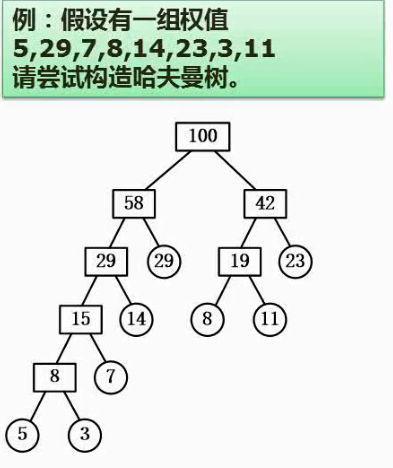
8,线索二叉树
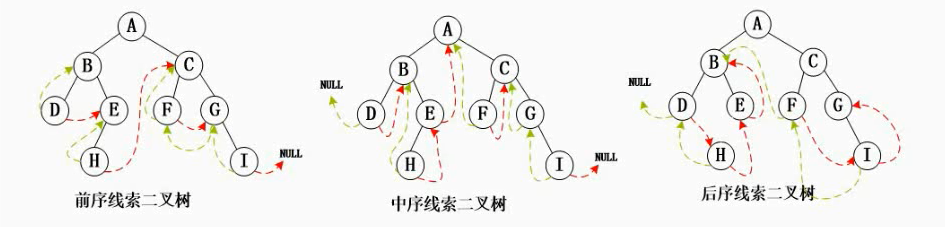
9,平衡二叉树



