后缀数组主要是两个数组:(sa)和(rk)
其中,(sa[i])表示将所有后缀排序后第(i)小的后缀的编号,(rk[i])表示后缀(i)的排名
这两个数组满足性质:(sa[rk[i]] = ra[sa[i]] = i)
后缀数组示例:
后缀数组的求法
(O(n^2logn))做法:
这个做法大家都会,暴力嘛,用(string + sort)就可以了
(O(nlog^2n))做法:
这个做法用到了倍增的思想
先对每个字符(长度为1的子串)进行排序
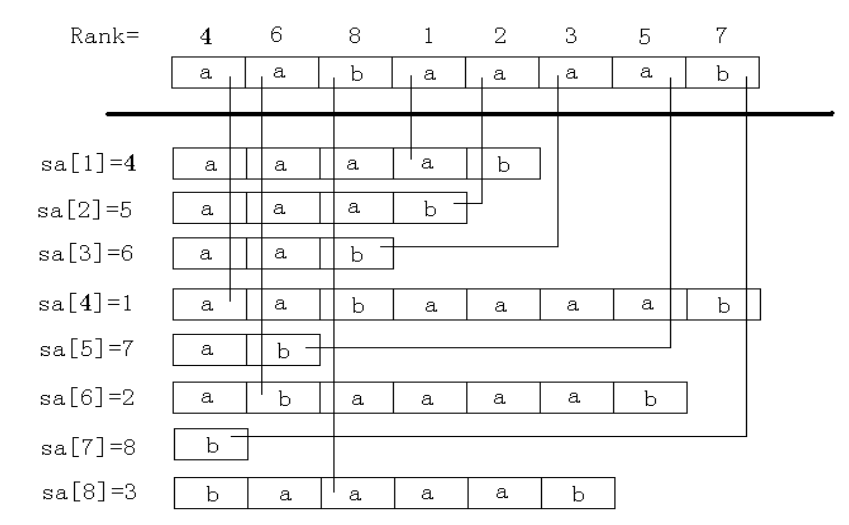
假设我们已经知道了长度为(w)的子串的排名(rk_w[1…n])(即,(rk_w[i])表示(s[i…min(i + w - 1,n)])在({s[x…min(x +w - 1,n)|xin[1,n]})中的排名),那么以(rk_w[i])为第一关键字,(rk_w[i+w])为第二关键字(若(i+w>n)则令(rk_w[i+w])为无穷小)进行排序,就可以求出(rk_2w[1…n])
倍增排序示意图:

如果用(sort)进行排序,复杂度就是(O(nlog^2n))
#define B cout << "BreakPoint" << endl;
#define O(x) cout << #x << " " << x << endl;
#define O_(x) cout << #x << " " << x << " ";
#define Msz(x) cout << "Sizeof " << #x << " " << sizeof(x)/1024/1024 << " MB" << endl;
#include<cstdio>
#include<cmath>
#include<iostream>
#include<cstring>
#include<algorithm>
#include<queue>
#include<set>
#define LL long long
const int inf = 1e9 + 9;
const int N = 2e5 + 5;
using namespace std;
inline int read() {
int s = 0,w = 1;
char ch = getchar();
while(ch < '0' || ch > '9') {
if(ch == '-')
w = -1;
ch = getchar();
}
while(ch >= '0' && ch <= '9') {
s = s * 10 + ch - '0';
ch = getchar();
}
return s * w;
}
char s[N];
int n,w,p,sa[N],rk[N << 1],oldrk[N << 1];
// 为了防止访问 rk[i+w] 导致数组越界,开两倍数组。
// 当然也可以在访问前判断是否越界,但直接开两倍数组方便一些。
int main() {
scanf("%s", s + 1);
n = strlen(s + 1);
for(int i = 1; i <= n; i++) rk[i] = s[i];
for(w = 1; w < n; w <<= 1) {
for(int i = 1; i <= n; i++) sa[i] = i;
sort(sa + 1, sa + n + 1,[](int x, int y) {return rk[x] == rk[y] ? rk[x + w] < rk[y + w] : rk[x] < rk[y];});
memcpy(oldrk, rk, sizeof(rk));
// 由于计算 rk 的时候原来的 rk 会被覆盖,要先复制一份
for(int i = 1;i <= n;i++) {
p = 0;
if(oldrk[sa[i]] == oldrk[sa[i - 1]] && oldrk[sa[i] + w] == oldrk[sa[i - 1] + w]) rk[sa[i]] = p;
else rk[sa[i]] = ++p; // 若两个子串相同,它们对应的 rk 也需要相同,所以要去重
}
}
for(int i = 1; i <= n; i++) printf("%d ", sa[i]);
return 0;
}
(O(nlogn))做法
在(O(nlog^2n))做法中,单次排序是(O(nlogn))的,如果能(O(n))排序即可
前置芝士:基数排序,计数排序
然而我也不会这个做法。
就这地吧
后缀数组
寻找最小的循环移动位置
将字符串(s)复制一份变成(ss)就转化成了后缀排序问题
例题: JSOI2007」字符加密 。
在字符串中找子串
任务 在线地在主串(T)中寻找模式串(S)。在线的意思是,我们已经预先知道主串(T),但是当且晋档询问时才知道模式串(S)。我们可以先构造出(T)的后缀数组,然后查找子串(S)。若子串(S)在(T)中出现,它必定是(T)的一些后缀的前缀。因为我们已将所有后缀排序了,我们额可以在通过(p)数组中二分(S)来实现。比较子串(S)和当前后缀的时间复杂度为(O(|S|)),因此找子串的时间复杂度为(O(|s|log|T|))。注意,如果该子串在(T)中国出现了多次,每次出现都是在(p)数组中相邻的。因此出现次数可以通过再次二分找到,输出每次出现的位置也很轻松。
从字符串首位取字符最小化字典序
例题: 「USACO07DEC」Best Cow Line 。
题意:给你一个字符串,每次从首或尾取一个字符组成字符串,问所有能够组成的字符串中字典序最小的一个。
暴力做法就是每次最坏(O(n))地判断当前应该取首还是尾(即比较取首得到的字符串与取尾得到的反串的大小),只需优化这一判断过程即可。
由于需要在原串后缀与反串后缀构成的集合内比较大小,可以将反串拼接在原串后,并在中间加上一个没出现过的字符(如 #,代码中可以直接使用空字符),求后缀数组,即可(O(1))完成这一判断。
height数组
LCP(最长公共前缀)
两个字符串(S)和(T)的LCP就是最大的(x)((x leq min(|S|,|T|)))使得(S_i = T_i(forall1leq ileq x))
(lcp(i,j))表示后缀(i)和后缀(j)的最长公共前缀(的长度)
height数组的定义
(height[i] = lcp(sa[i],sa[i-1])),即第(i)名的后缀与它前一名的后缀的最长公共前缀。
(height[1])可以视作0
(O(n))求(height)数组需要一个引理
(height[rk[i]] ge height[rk[i - 1]] - 1)
证明:
当(height[rk[i-1]]leq 1)时,上式显然成立(右边小于等于0)
当(height[rk[i - 1]]>1)时:
设后缀(i-1)为(aAD)((A)是一个长度为(height[rk[i-1]]-1)的字符串),那么后缀(i)就是(AD)。设后缀(sa[rk[i-1]-1])为(aAB),那么(lcp(i - 1,sa[rk[i-1]-1])=aA)。由于后缀(sa[rk[i-1]-1]+1)是(AB),一定飘在后缀(i)的前面,所后缀数组(sa[rk[i]-1])一定含有前缀(A),所以(lcp(i,sa[rk[i]-1]))至少是(height[rk[i-1]]-1)。
(O(n))求height数组的代码实现
利用上面这个引理暴力求:
for(int i = 1, k = 0; i <= n; ++i) {
if (k) --k;
while(s[i + k] == s[sa[rk[i] - 1] + k]) ++k;
ht[rk[i]] = k; // height太长了缩写为ht
}
(k)不会超过(n),最多减(n)次,所以最多加(2n)次,总复杂度就是(O(n))。
height数组的应用
两子串最长公共前缀
(lcp(sa[i],sa[j]) = min{ height[i+1…j]})
感性理解:如果(height)一直大于某个数,前这么多为一直就没变过;反之,由于后缀已经排好序了,不可能变了之后变回来。
有了这个定理,求两子串最长公共前缀就转化为了RMQ问题
比较一个字符串的两个子串的大小关系
假设需要比较的是(A=S[a..b])和(B=S[c..d])的大小关系。
若(lcp(a,c) ge min(|A|,|B|),A<B iff |A| < |B|)
否则,(A<B iff rk[a] < rk[b])
不同子串的数目
子串就是后缀的前缀,所以可以每个后缀,计算前缀总数,再减掉重复。
“前缀总数”其实就是子串个数,为(n(n+1)/2)
如果按后缀排序的顺序枚举后缀,每次新增的子串就是除了与上一个后缀的LCP剩下的前缀。这些前缀一定是新增的,否则会破坏(lcp(sa[i],s[j])=min{ height[i+1..j]})的性质。只有这些前缀是新增的,因为LCP部分在枚举上一个前缀时计算过了
所以答案为