4.1 深度学习与深层神经网络
维基百科对深度学习的精确定义为“一类通过多层非线性变换对高复杂性数据建模算法的合集”。因为深层神经网络是实现“多层非线性变化”最常用的一种方法,所以在实际中基本可以认为深度学习就是深层神经网络的代名词.
4.2 损失函数定义
(1)经典损失函数
通过神经网络解决多分类问题最常用的方法是设置n个输出节点,其中n为类别的个数,对于每一个样例,神经网络可以得到一个n维数组作为输出结果,数组中的每一个维度对应一个类别。如何判断一个输出向量和期望向量有多接近呢?交叉熵是常用的批判方法之一。
H(p,q)=-∑p(x)log q(x) :通过概率分布q来表达概率分布p的困难程度,p代表正确答案,q代表预测值,交叉熵值越小,两个概率分布越接近。
Softmax回归本身可以作为一个学习算法来优化分类结果,但在TensorFlow中,Softmax回归的参数被去掉了,它只是一层额外的处理层,将神经网络的输出变成一个概率分布。
softmax(yi)=yi'=eyi/(∑j=1n eyj):这样就把神经网络的输出变成了一个概率分布,从而可以通过交叉熵来计算预测的概率分布和真实答案的概率分布之间的距离了。
cross_entropy=-tf.reduce_mean(y_*tf.log(tf.clip_by_value(y,1e-10,1.0)))
因为交叉熵一般会与softmax回归一起使用,所以tf对这两个功能进行了同一封装:
cross_entropy=tf.nn.softmax_cross_entropy_with_logits(y,y_)
与分类问题不同,回归问题解决的是对具体数值的预测。解决回归问题的神经网络一般只有一个输出节点,这个节点的输出值就是预测值。
对于回归问题,最常用的损失函数是均方误差(MSE,mean squared error):MSE(y,y')=∑ni=1(yi-y'i)^2/n
mse=tf.reduce_mean(tf.square(y_-y))
(2)自定义损失函数
通过自定义损失函数可以使神经网络优化的结果更加接近实际问题的需求。
比如一个商品成本是一元,但是利润是十元,那么少预测一个就少挣十元;而多预测一个才少挣一元。
loss=tf.reduce_sum(tf.select(tf.greater(v1,v2),(v1-v2)*10,(v2-v1)))
(tf.greater会比较两个输入张量中的每一个元素的大小,并返回比较结果)
下面有一个简单的神经网络程序来讲解损失函数对模型训练结果的影响:

import tensorflow as tf from numpy.random import RandomState batch_size = 8 x = tf.placeholder(tf.float32, shape=(None, 2), name="x-input") y_ = tf.placeholder(tf.float32, shape=(None, 1), name='y-input') w1= tf.Variable(tf.random_normal([2, 1], stddev=1, seed=1)) y = tf.matmul(x, w1) # 定义损失函数使得预测少了的损失大,于是模型应该偏向多的方向预测。 loss_less = 10 loss_more = 1 loss = tf.reduce_sum(tf.where(tf.greater(y, y_), (y - y_) * loss_more, (y_ - y) * loss_less)) train_step = tf.train.AdamOptimizer(0.001).minimize(loss) #设置回归的正确值为两个输入的和加上一个随机量 rdm = RandomState(1) X = rdm.rand(128,2) Y = [[x1+x2+(rdm.rand()/10.0-0.05)] for (x1, x2) in X] with tf.Session() as sess: init_op = tf.global_variables_initializer() sess.run(init_op) STEPS = 5000 for i in range(STEPS): start = (i*batch_size) % 128 end = (i*batch_size) % 128 + batch_size sess.run(train_step, feed_dict={x: X[start:end], y_: Y[start:end]}) if i % 1000 == 0: print("After %d training step(s), w1 is: " % (i)) print sess.run(w1), " " print "Final w1 is: ", sess.run(w1) -------------------------------------------------------------------- After 0 training step(s), w1 is: [[-0.81031823] [ 1.4855988 ]] After 1000 training step(s), w1 is: [[ 0.01247112] [ 2.1385448 ]] After 2000 training step(s), w1 is: [[ 0.45567414] [ 2.17060661]] After 3000 training step(s), w1 is: [[ 0.69968724] [ 1.8465308 ]] After 4000 training step(s), w1 is: [[ 0.89886665] [ 1.29736018]] Final w1 is: [[ 1.01934695] [ 1.04280889]] --------------------------------------------------------------------- #重新定义损失函数,使得预测多了的损失大,于是模型应该偏向少的方向预测。 loss_less = 1 loss_more = 10 loss = tf.reduce_sum(tf.where(tf.greater(y, y_), (y - y_) * loss_more, (y_ - y) * loss_less)) train_step = tf.train.AdamOptimizer(0.001).minimize(loss) with tf.Session() as sess: init_op = tf.global_variables_initializer() sess.run(init_op) STEPS = 5000 for i in range(STEPS): start = (i*batch_size) % 128 end = (i*batch_size) % 128 + batch_size sess.run(train_step, feed_dict={x: X[start:end], y_: Y[start:end]}) if i % 1000 == 0: print("After %d training step(s), w1 is: " % (i)) print sess.run(w1), " " print "Final w1 is: ", sess.run(w1) ----------------------------------------------------------------------- After 0 training step(s), w1 is: [[-0.81231821] [ 1.48359871]] After 1000 training step(s), w1 is: [[ 0.18643527] [ 1.07393336]] After 2000 training step(s), w1 is: [[ 0.95444274] [ 0.98088616]] After 3000 training step(s), w1 is: [[ 0.95574027] [ 0.9806633 ]] After 4000 training step(s), w1 is: [[ 0.95466018] [ 0.98135227]] Final w1 is: [[ 0.95525807] [ 0.9813394 ]] ------------------------------------------------------------------- #定义损失函数为MSE loss = tf.losses.mean_squared_error(y, y_) train_step = tf.train.AdamOptimizer(0.001).minimize(loss) with tf.Session() as sess: init_op = tf.global_variables_initializer() sess.run(init_op) STEPS = 5000 for i in range(STEPS): start = (i*batch_size) % 128 end = (i*batch_size) % 128 + batch_size sess.run(train_step, feed_dict={x: X[start:end], y_: Y[start:end]}) if i % 1000 == 0: print("After %d training step(s), w1 is: " % (i)) print sess.run(w1), " " print "Final w1 is: ", sess.run(w1) ------------------------------------------------------------------------ After 1000 training step(s), w1 is: [[-0.13337609] [ 1.81309223]] After 2000 training step(s), w1 is: [[ 0.32190299] [ 1.52463484]] After 3000 training step(s), w1 is: [[ 0.67850214] [ 1.25297272]] After 4000 training step(s), w1 is: [[ 0.89473999] [ 1.08598232]] Final w1 is: [[ 0.97437561] [ 1.0243336 ]]
4.3 神经网络优化算法
梯度下降算法(gradient decent)主要用于优化单个参数的取值,而反向传播算法(backpropagation)给出了一个高效的方式在所有参数上使用梯度下降算法,从而使神经网络模型在训练数据上的损失函数尽可能小。
需要注意的是,梯度下降算法并不能保证被优化的函数达到全局最优解,可能掉进局部最优,只有当损失函数为凸函数,梯度下降算法才能保证达到全局最优解。
除了不一定能达到全局最优外,梯度下降算法的另一个问题就是计算时间太长。为了加速训练过程,可以使用随机梯度下降算法(stochastic gradient descent),这个算法优化的不是在全部训练数据上的损失函数,而是在每一轮迭代中,随机优化每一小部分训练数据上的损失函数。这一小部分数据称为一个batch。
4.4 神经网络的进一步优化
(1)学习率的设置
指数衰减法(tf.train.exponential_decay)可以先使用较大的学习率来快速得到一个比较优的解,然后随着迭代的继续逐步减小学习率,使得模型在后期更加稳定:
每一轮优化时的学习率:decayed_learning_rate=learning_rate初始学习率*decay_rate衰减速度^(global_step/decay_steps衰减速度)
tf.train.exponential_decay函数可以通过设置参数staircase选择不同的衰减方式。
通常decay_steps代表了完整的使用一遍训练数据所需要的迭代轮数(总样本数除以一个batch中的训练样本数)

#假设我们要最小化函数 y=x2y=x2, 选择初始点 x0=5 #1. 学习率为1的时候,x在5和-5之间震荡。 import tensorflow as tf TRAINING_STEPS = 10 LEARNING_RATE = 1 x = tf.Variable(tf.constant(5, dtype=tf.float32), name="x") y = tf.square(x) train_op = tf.train.GradientDescentOptimizer(LEARNING_RATE).minimize(y) with tf.Session() as sess: sess.run(tf.global_variables_initializer()) for i in range(TRAINING_STEPS): sess.run(train_op) x_value = sess.run(x) print "After %s iteration(s): x%s is %f."% (i+1, i+1, x_value) After 1 iteration(s): x1 is -5.000000. After 2 iteration(s): x2 is 5.000000. After 3 iteration(s): x3 is -5.000000. After 4 iteration(s): x4 is 5.000000. After 5 iteration(s): x5 is -5.000000. After 6 iteration(s): x6 is 5.000000. After 7 iteration(s): x7 is -5.000000. After 8 iteration(s): x8 is 5.000000. After 9 iteration(s): x9 is -5.000000. After 10 iteration(s): x10 is 5.000000. ------------------------------------------------------------------------ 2.学习率为0.001的时候,下降速度过慢,在901轮时才收敛到0.823355。 TRAINING_STEPS = 1000 LEARNING_RATE = 0.001 x = tf.Variable(tf.constant(5, dtype=tf.float32), name="x") y = tf.square(x) train_op = tf.train.GradientDescentOptimizer(LEARNING_RATE).minimize(y) with tf.Session() as sess: sess.run(tf.global_variables_initializer()) for i in range(TRAINING_STEPS): sess.run(train_op) if i % 100 == 0: x_value = sess.run(x) print "After %s iteration(s): x%s is %f."% (i+1, i+1, x_value) After 1 iteration(s): x1 is 4.990000. After 101 iteration(s): x101 is 4.084646. After 201 iteration(s): x201 is 3.343555. After 301 iteration(s): x301 is 2.736923. After 401 iteration(s): x401 is 2.240355. After 501 iteration(s): x501 is 1.833880. After 601 iteration(s): x601 is 1.501153. After 701 iteration(s): x701 is 1.228794. After 801 iteration(s): x801 is 1.005850. After 901 iteration(s): x901 is 0.823355. ----------------------------------------------------------------------- 3. 使用指数衰减的学习率,在迭代初期得到较高的下降速度,可以在较小的训练轮数下取得不错的收敛程度。 TRAINING_STEPS = 100 global_step = tf.Variable(0) LEARNING_RATE = tf.train.exponential_decay(0.1, global_step, 1, 0.96, staircase=True) x = tf.Variable(tf.constant(5, dtype=tf.float32), name="x") y = tf.square(x) train_op = tf.train.GradientDescentOptimizer(LEARNING_RATE).minimize(y, global_step=global_step) with tf.Session() as sess: sess.run(tf.global_variables_initializer()) for i in range(TRAINING_STEPS): sess.run(train_op) if i % 10 == 0: LEARNING_RATE_value = sess.run(LEARNING_RATE) x_value = sess.run(x) print "After %s iteration(s): x%s is %f, learning rate is %f."% (i+1, i+1, x_value, LEARNING_RATE_value) After 1 iteration(s): x1 is 4.000000, learning rate is 0.096000. After 11 iteration(s): x11 is 0.690561, learning rate is 0.063824. After 21 iteration(s): x21 is 0.222583, learning rate is 0.042432. After 31 iteration(s): x31 is 0.106405, learning rate is 0.028210. After 41 iteration(s): x41 is 0.065548, learning rate is 0.018755. After 51 iteration(s): x51 is 0.047625, learning rate is 0.012469. After 61 iteration(s): x61 is 0.038558, learning rate is 0.008290. After 71 iteration(s): x71 is 0.033523, learning rate is 0.005511. After 81 iteration(s): x81 is 0.030553, learning rate is 0.003664. After 91 iteration(s): x91 is 0.028727, learning rate is 0.002436.
一般来说初始学习率、衰减系数和衰减速度都是根据经验设置,且不能通过前几轮损失函数下降的速度来比较不同神经网络的效果。
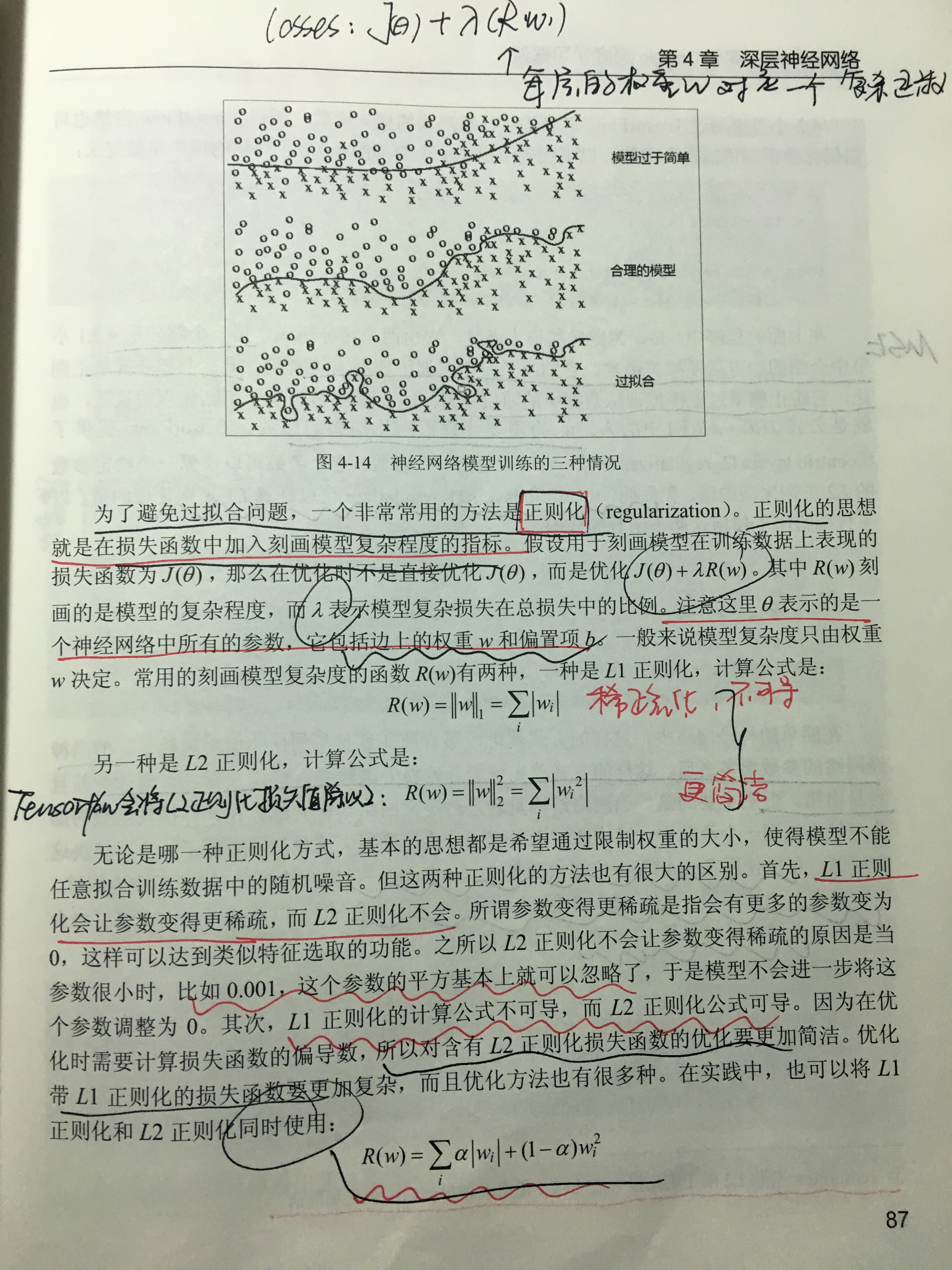
(2)过拟合问题
所谓过拟合,指的是当一个模型过为复杂之后,它可以很好地“记忆”每一个训练数据中随机噪音的部分而忘记了要去“学习”训练数据中的通用的趋势。
import tensorflow as tf def get_weight(shape,lambda1): var=tf.Variable(tf.random_normal(shape),dtype=tf.float32) tf.add_to_collection('losses',tf.contrib.layers.l2_regularizer(lambda1)(var)) return var x=tf.placeholder(tf.float32,shape=(None,2)) y_=tf.placeholder(tf.float32,shape=(None,1)) batch_size=8 layer_dimension=[2,10,10,10,1] n_layers=len(layer_dimension) cur_layer=x in_dimension=layer_dimension[0] for i in range(1,n_layers): out_dimension=layer_dimension[i] weight=get_weight([in_dimension,out_dimension],0.001) bias=tf.Variable(tf.constant(0.1,shape=[out_dimension])) cur_layer=tf.nn.relu(tf.matmul(cur_layer,weight)+bias) in_dimension=layer_dimension[i] mse_loss=tf.reduce_mean(tf.square(y_-cur_layer)) tf.add_to_collection('losses',mse_loss) loss=tf.add_n(tf.get_collection('losses'))
(3)滑动平均模型
在采用随机梯度下降算法训练神经网络时,使用滑动平均模型在很多应用中都可以在一定程度提高最终模型在测试数据上的表现。
这里有篇博客总结的不错也很简短:TensorFlow中滑动平均模型介绍
这一章从神经网络模型结构的设计、损失函数的设计、神经网络的优化和神经网络的进一步调优四个方面覆盖了设计和优化神经网络过程中可能遇到的主要问题。
