第十二章 栈与队列
- 数据结构的概念
数据结构(Data Structure)是数据的组织形式。程序中用到的数据都不是孤立的,而是有相互联系的,根据访问数据需求不同,同样的数据可以有多种不同的组织方式。复合类型也可以看作是数据的组织方式,把同一类型的数据组织成数组,或者把描述同一对象的各成员组织成结构体。数据的组织方式包含了存储方式和访问方式这两层意思,二者是紧密联系的。例如,数组的各元素是一个挨一个存储的,并且每个元素的大小相同,因此数组可以提供按下标访问的方式,结构体的各成员也是一个挨一个存储的,但是每个成员的大小不同,所以只能用.运算符加成员名来访问,而不能按下标访问。
一个问题中数据的存储方式和访问方式就决定了解决问题可以采用什么样的算法,要设计一个算法就要同时设计相应的数据结构来支持这种算法。所以Pascal语言的设计者Niklaus Wirth提出算法+数据结构=程序。
2.堆栈
堆栈是一组元素的集合,类似于数组,不同之处在于数组可以按下标随机访问,这次访问a[5]下次可以访问a[1],但是堆栈的访问规则被限制为Push和Pop两种操作,Push(入栈或压栈)向栈顶添加元素,Pop(出栈或弹出)则取出当前栈顶的元素,也就是说,只能访问栈顶元素而不能访问栈中其他元素。如果所有元素的类型相同,堆栈的存储也可以用数组来实现,访问操作可以通过函数接口提供。如用堆栈实现倒序打印:

运行结果是cba。运行过程图示如下:
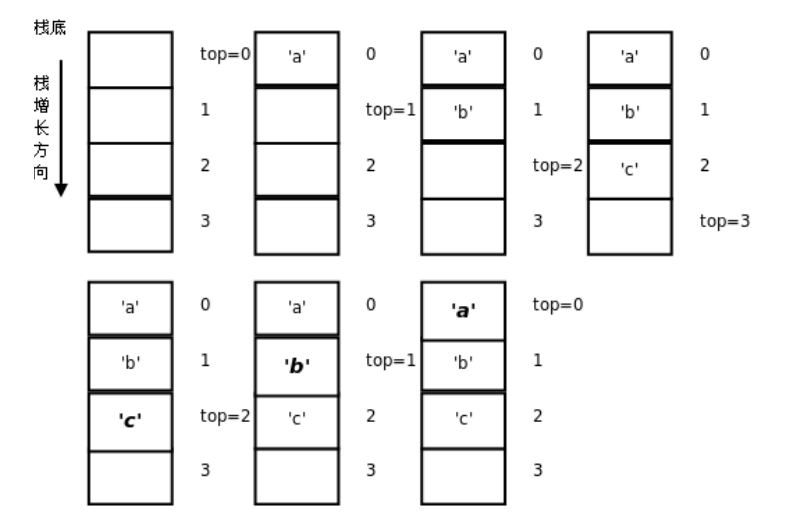
数组stack是堆栈的存储空间,top用作数组stack的索引,注意top总是指向栈顶元素的下一个元素,可以把它称为指针(Pointer)。这里的“top总是指向栈顶元素的下一个元素”其实也是一种Invariant,可以检验Push和Pop操作是否正确实现了,这种Invariant表示一个数据结构的状态总是维持某个条件,在DbC中称为Class Invariant。Pop操作的语义是取出栈顶元素,但上例的实现其实并没有清除原来的栈顶元素,只是把top指针移动了一下,原来的栈顶元素仍然存在那里。这就足够了,因为此后通过Push和Pop操作不可能再访问到已经取出的元素了,下次Push操作就会覆盖它。putchar函数的作用是把一个字符打印到屏幕上,和printf的%c作用相同。布尔函数is_empty的作用是防止Pop操作访问越界。这里我们把栈的空间取得足够大(512个元素),其实严格来说Push操作也应该检查是否越过上界。
在main函数中,入栈的顺序是‘a’、’b’、’c’,而出栈打印的顺序却是‘c’、‘b’、’a’,最后入栈的‘c’最早出来,因此堆栈这种数据结构的特点可以概括为LIFO(Last In First Out,后进先出)。我们也可以写一个递归函数来倒序打印,这是利用函数调用的栈帧实现后进先出:
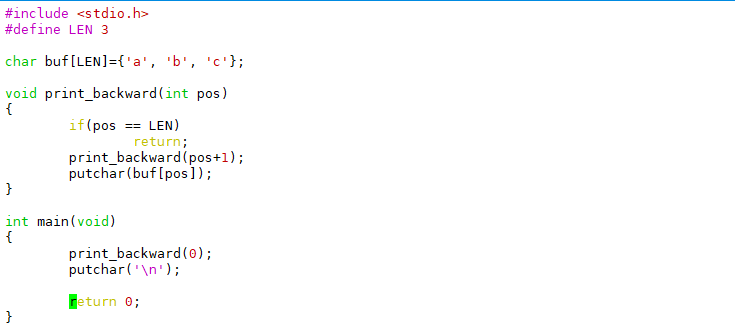
也许你会说,又是堆栈又是递归的,倒序打印一个数组犯得着这么大动干戈吗?写一个简单的循环不就行了:

对于数组来说确实没必要搞这么复杂,但对于某些数据结构就没这么简单了。
3.深度优先搜索
现在我们用堆栈解决一个有意思的问题,定义一个二维数组:

它表示一个迷宫,其中的1表示墙壁,0表示可以走的路,只能横着走或竖着走,不能斜着走,要求编程序找出从左上角到右下角的路线。程序如下:
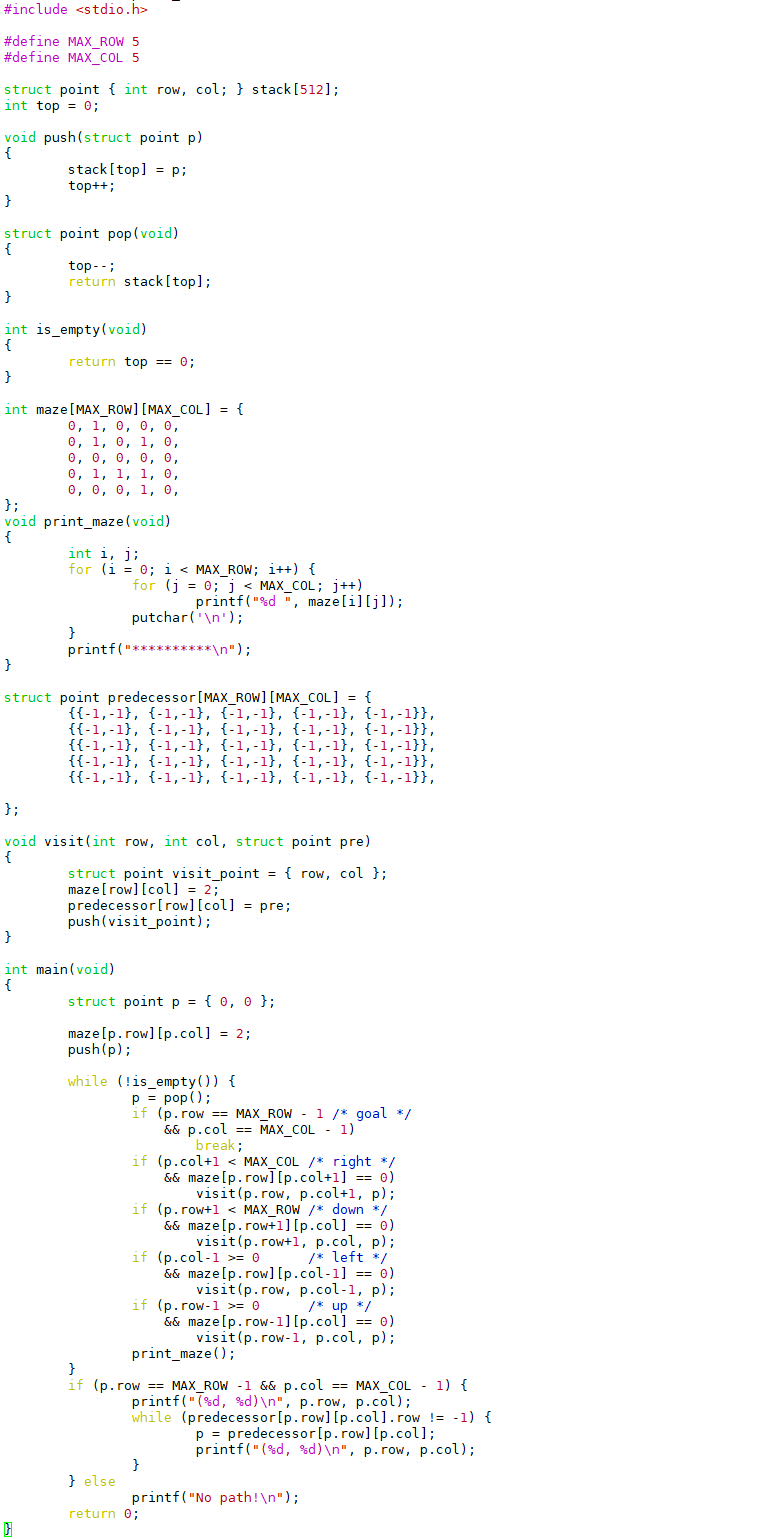
运行结果如下:

这次堆栈里的元素是结构体类型的,用来表示迷宫中一个点的x和y坐标。我们用一个新的数据结构保存走迷宫的路线,每个走过的点都有一个前趋(Predecessor)的点,表示是从哪儿走到当前点的,比如predecessor[4][4]是座标为(3,4)的点,就表示从(3,4)走到了(4,4),一开始predecessor的各元素初始化为无效座标(-1,-1)。在迷宫中探索路线的同时就把路线保存在predecessor数组中,已经走过的点在maze数组中标记为2防止重复走,最后找到终点时就根据predecessor数组保存的路线从终点打印到起点。为了帮助理解,我们把这个算法改写成伪代码如下:

我在while循环的末尾插入了打印语句,每探索一步都打印出当前标记了哪些点,从打印结果可看出这种搜索算法的特点:每次取一个相邻的点走下去,一直走到无路可走了再退回来,取另一个相邻的点再走下去。这称为深度优先搜索(DFS, Depth First Search)。探索迷宫和堆栈变化的过程如下图所示。
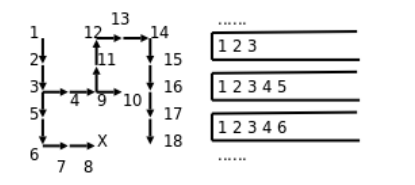
图中各点的编号反映出探索的顺序,堆栈中的数字就是图中点的编号,可见正是因为堆栈后进先出的性质使这个算法具有了深度优先的特点。如果在探索问题的解时走进了死胡同,则需要退回来从另一条路继续探索,这种思想称为回溯(Backtrack)。
如果在一个循环里打印数组,既可以正向打印也可以反向打印,因为数组这种数据结构是支持随机访问的,当然也支持顺序访问,并且既可以是正向的也可以是反向的。但现在predecessor这种数据结构的每个元素只知道它的前趋是谁,而不知道它的后继(Successor)是谁,所以在循环里只能反向打印。由此可见,有什么样的数据结构就决定了可以用什么样的算法。设计算法和设计数据结构这两件工作是紧密联系的。
4.队列与广度优先搜索
队列也是一组元素的集合,也提供两种基本操作:Enqueue(入队)将元素添加到队尾,Dequeue(出队)从队头取出元素并返回。就像排队买票一样,先来先服务,先入队的人也是先出队的,这种方式称为FIFO(First In First Out,先进先出),有时候队列本身也被称为FIFO。下面我们用队列解决迷宫问题。程序如下:
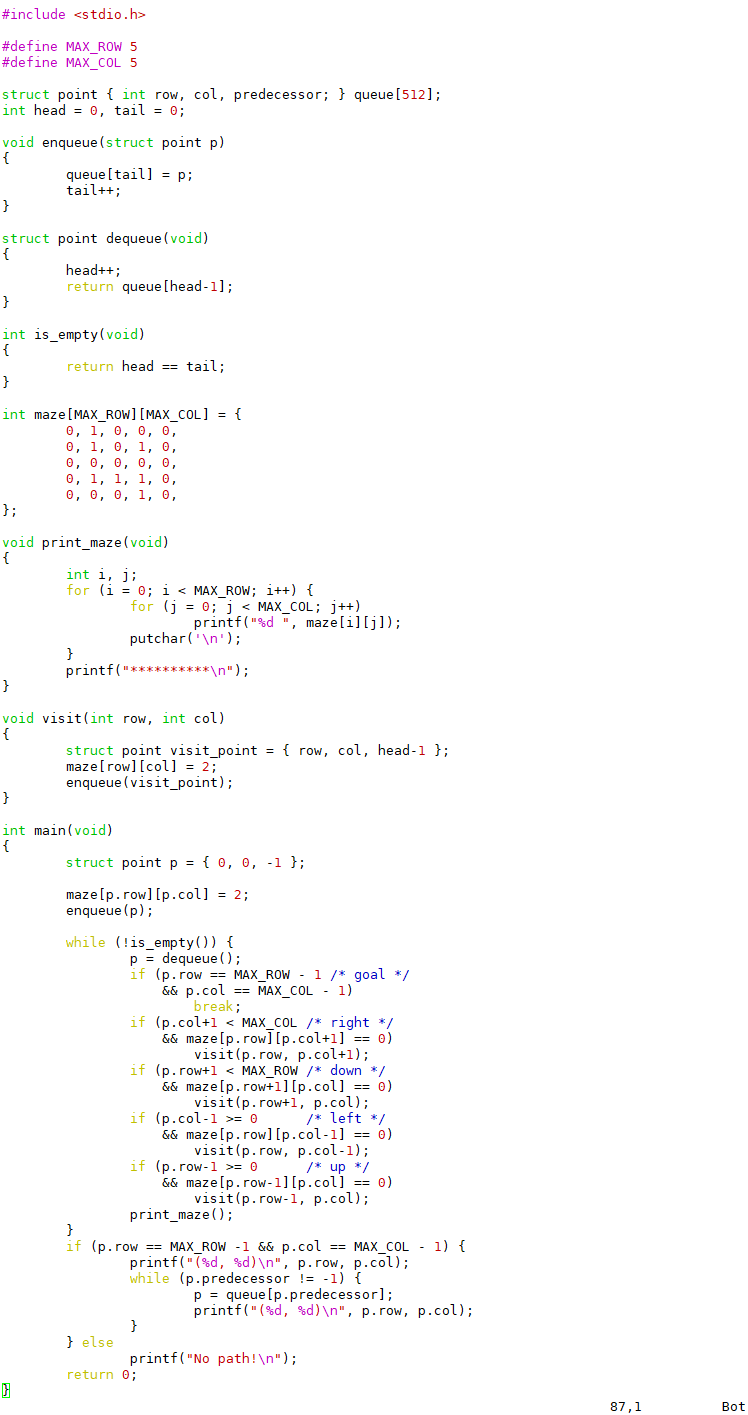
运行结果如下:

其实仍然可以像前面“用深度优先搜索解迷宫问题”一样用predecessor数组表示每个点的前趋,但是我们换一种更方便的数据结构,直接在每个点的结构体中加一个成员表示前趋:

变量head、tail就像前两节用来表示栈顶的top一样,是queue数组的索引或者叫指针,分别指向队头和队尾。每个点的predecessor成员也是一个指针,指向它的前趋在queue数组中的位置:
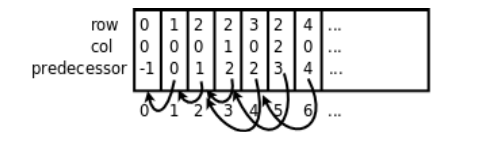
为了帮助理解,我们把这个算法改写成伪代码如下:

从打印的搜索过程可以看出,这个算法的特点是沿各个方向同时展开搜索,每个可以走通的方向轮流往前走一步,这称为广度优先搜索(BFS,Breadth First Search)。探索迷宫和队列变化的过程如下图所示。
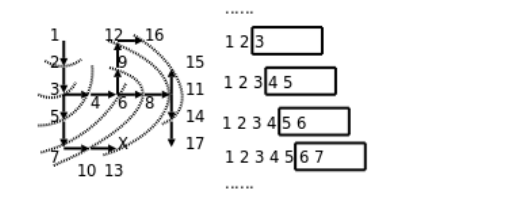
广度优先是一种步步为营的策略,每次都从各个方向探索一步,将前线推进一步,图中的虚线就表示这个前线,队列中的元素总是由前线的点组成,可见正是因为队列先进先出的性质使这个算法具有了广度优先的特点。广度优先搜索还有一个特点是可以找到从起点到终点的最短路径,而深度优先搜索找到的不一定是最短路径。
5.环形队列
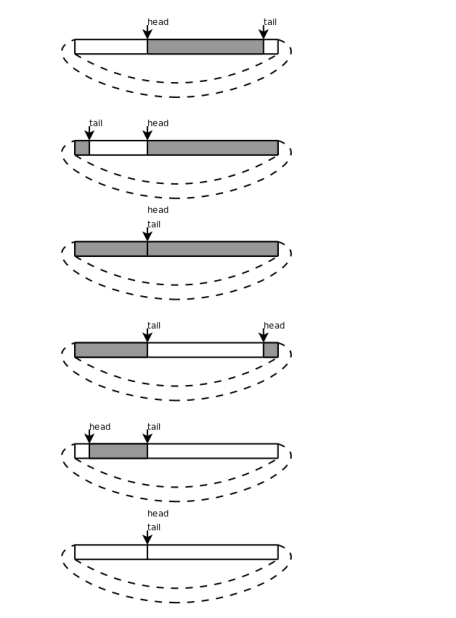
比较“用深度优先搜索解迷宫问题”的栈操作和“用广度优先搜索解迷宫问题”的队列操作可以发现,栈操作的top指针在Push时增大而在Pop时减小,栈空间是可以重复利用的,而队列的head、tail指针都在一直增大,虽然前面的元素已经出对了,但它所占的存储空间却不能重复利用。在“用广度优先搜索解迷宫问题”的揭发中,出队的元素仍然有用,保存着走过的路径和每个点的前趋,但大多数程序并不是这样使用队列的,一般情况下出队的元素就不再有保存价值了,这些元素的存储空间应该回收利用,因此我们介绍一种新的数据结构——环形队列(Circular Queue)。把queue数组想想成一个圈,head和tail指针仍然是一直增大的,当指到数组末尾时就自动回到数组开头,就像两个人围着操场赛跑,沿着它们跑的方向看,从head到tail之间是队列的有效元素,从tail到head之间是空的存储位置,head追上tail就表示队列空了,tail追上head就表示队列的存储空间满了。
环形队列: