Leetcode 之 Combination Sum系列

39. Combination Sum

1.Problem

Find all possible combinations of k numbers that add up to a number n, given that only numbers from 1 to 9 can be used and each combination should be a unique set of numbers.

Example 1:

Input: k = 3, n = 7

Output:

[[1,2,4]]

Example 2:

Input: k = 3, n = 9

Output:

[[1,2,6], [1,3,5], [2,3,4]]

2.Solution

   题目的大意是给定一个元素不存在重复的一维数组candidates和一个目标数target，输出由一位数组中的数可以组成target的所有组合类型，注：candidates中的数可以重复使用的。

   对给定的数组进行排序，然后针对target进行回溯。

3.Code

package test;

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;

public class TaskTest {
    private List<List<Integer>> result = new ArrayList<List<Integer>>();
    private int[] temp;
    public static void main(String[] args) {
        int[] a = {2,3,6,7};
        
        new TaskTest().combinationSum(a,7);
        //System.out.println();
    }
    
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        //[2, 3, 6, 7] and target 7
        this.temp = candidates;
        Arrays.sort(temp);
        List<Integer> current = new ArrayList<>();
        backTracing(current,0,target);
        System.out.println(this.result.toString());
        return result;
    }
    
    public void backTracing(List<Integer> current , int index , int target) {
        if ( target == 0 ) {
            List<Integer> list = new ArrayList<>(current);
            result.add(list);
        } else {
            for ( int i = index ; i < temp.length && temp[i] <= target ; i++ ) {
                current.add(temp[i]);
                backTracing(current,i,target - temp[i]);
                current.remove(new Integer(temp[i]));
            }
        }
    }
}

4.提交Leetcode的代码

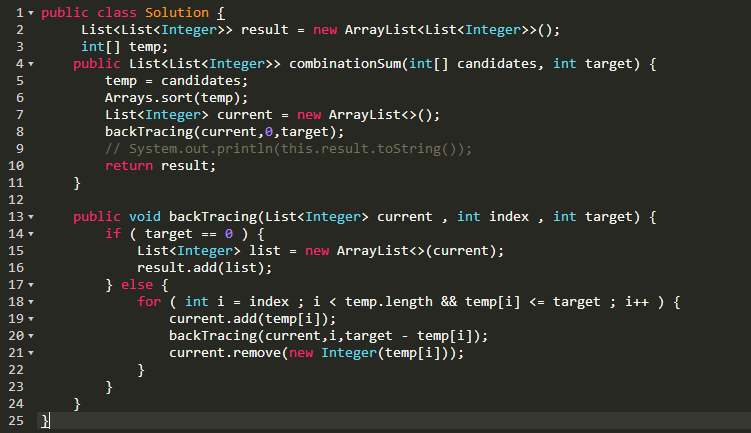
 40. Combination Sum II

1.Problem

Given a collection of candidate numbers (C) and a target number (T), find all unique combinations in C where the candidate numbers sums to T.

Each number in C may only be used once in the combination.

Note:

• All numbers (including target) will be positive integers.
• The solution set must not contain duplicate combinations.

For example, given candidate set [10, 1, 2, 7, 6, 1, 5] and target 8,
A solution set is:

[
  [1, 7],
  [1, 2, 5],
  [2, 6],
  [1, 1, 6]
]

2.Soluton

   Combination Sum II跟 I比不同点在于，II中的一维数组中元素允许重复，但是组成target的每个元素仅允许被使用一次

1. backTracing(current,i + 1 ,target - temp[i]); 位置变为 i + 1
2. 处理结果中存在的重复问题
3. 输出的结果跟顺序无关，即([[1,1,6],[1,2,5],[1,7],[2,6]]) 和([[1,2,5],[1,1,6],[2,6],[1,7]])是相同的，都是正确的结果

3.Code

package test;

import java.util.ArrayList;
import java.util.Arrays;
import java.util.HashSet;
import java.util.Iterator;
import java.util.List;
import java.util.Set;

public class TaskTest {
    private List<List<Integer>> result = new ArrayList<List<Integer>>();
    private int[] temp;
    public static void main(String[] args) {
        int[] a = {1,1,2,5,6,7,10};
        
        
        new TaskTest().combinationSum(a,8);
        //System.out.println();
    }
    
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        //[2, 3, 6, 7] and target 7
        this.temp = candidates;
        Arrays.sort(temp);
        List<Integer> current = new ArrayList<>();
        backTracing(current,0,target);
        System.out.println(this.result.toString());
        Set<List<Integer>> set = new HashSet<>();
        for (List<Integer> l : result ) {
            if ( !set.contains(l)) {
                set.add(l);
            }
        }
        System.out.println(set.toString());
        result.clear();
        Iterator<List<Integer>> i = set.iterator();
        while ( i.hasNext() ) {
          result.add(i.next());    
        }
        System.out.println(result.toString());
        return result;
    }
    
    public void backTracing(List<Integer> current , int index , int target) {
        if ( target == 0 ) {
            List<Integer> list = new ArrayList<>(current);
            result.add(list);
        } else {
            for ( int i = index ; i < temp.length && temp[i] <= target ; i++ ) {
                current.add(temp[i]);
                backTracing(current,i + 1 ,target - temp[i]);
                current.remove(new Integer(temp[i]));
            }
        }
    }
}

4.提交Leetcode的代码

  

216. Combination Sum III

1.Problem

Find all possible combinations of k numbers that add up to a number n, given that only numbers from 1 to 9 can be used and each combination should be a unique set of numbers.

 

Example 1:

Input: k = 3, n = 7

Output:

[[1,2,4]]

 

Example 2:

Input: k = 3, n = 9

Output:

[[1,2,6], [1,3,5], [2,3,4]]

2.Solution

   一维数组固定为{1,2,3,4,5,6,7,8,9}，要求了组成target的数的个数，同样要求数字不能重复使用

3.Code

package test;

import java.util.ArrayList;
import java.util.Arrays;
import java.util.HashSet;
import java.util.Iterator;
import java.util.List;
import java.util.Set;

public class TaskTest {
    private List<List<Integer>> result = new ArrayList<List<Integer>>();
    private int[] temp = {1,2,3,4,5,6,7,8,9};
    public static void main(String[] args) {
        new TaskTest().combinationSum(3,9);
        //System.out.println();
    }
    
    public List<List<Integer>> combinationSum(int k, int target) {
        //[2, 3, 6, 7] and target 7
        List<Integer> current = new ArrayList<>();
        backTracing(current,0,target);
        for ( int i = 0 ; i < result.size() ; i++ ) {
            List<Integer> l = result.get(i);
            
            if (l.size() != k ) {
                System.out.println(l.toString());
                result.remove(i);
                i--;
            }
        }
        System.out.println(result.toString());
        return result;
    }
    
    public void backTracing(List<Integer> current , int index , int target) {
        if ( target == 0 ) {
            List<Integer> list = new ArrayList<>(current);
            result.add(list);
        } else {
            for ( int i = index ; i < temp.length && temp[i] <= target ; i++ ) {
                current.add(temp[i]);
                backTracing(current,i + 1 ,target - temp[i]);
                current.remove(new Integer(temp[i]));
            }
        }
    }
}

4.提交Leetcode的代码

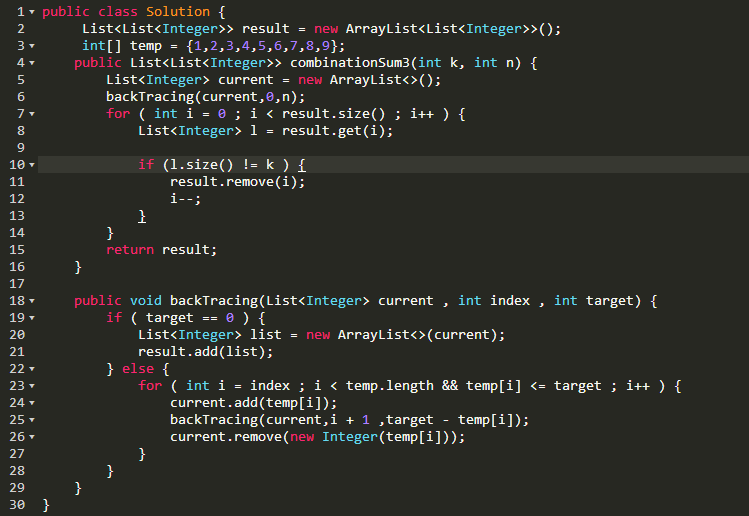
377. Combination Sum IV

1.Problem

Given an integer array with all positive numbers and no duplicates, find the number of possible combinations that add up to a positive integer target.

Example:

nums = [1, 2, 3]
target = 4

The possible combination ways are:
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)

Note that different sequences are counted as different combinations.

Therefore the output is 7.

2.Solution

   动态规划，转移方程为:dp[n] = dp[n] + dp[n-nums[k]] (dp[0] = 1, 即n - nums[k] == 0时 )，dp[i] 代表给定的数组能组成i的种类数

3.Code

class Solution {
    public int combinationSum4(int[] nums, int target) {
        int[] dp = new int[target + 1];
        dp[0] = 1;
        Arrays.sort(nums);
        DP(target , nums , dp);
        return dp[target];
    }

    public void DP ( int target , int[] nums , int[] dp ) {
       for ( int i = 1 ; i <= target ; i++ ) {
            for ( int j = 0 ; j < nums.length ; j++ ) {
                if ( i - nums[j] >= 0 ) {
                    dp[i] = dp[i] + dp[ i - nums[j] ];
                } else {
                    break;
                }
            }
       }
    }
}

//预先对nums进行排序然后循环中加break，leetcode 提交从18.02%提升到65.16%

4.提交Leetcode的代码