第一次使用 Matlab,遂将过程详细记录之。
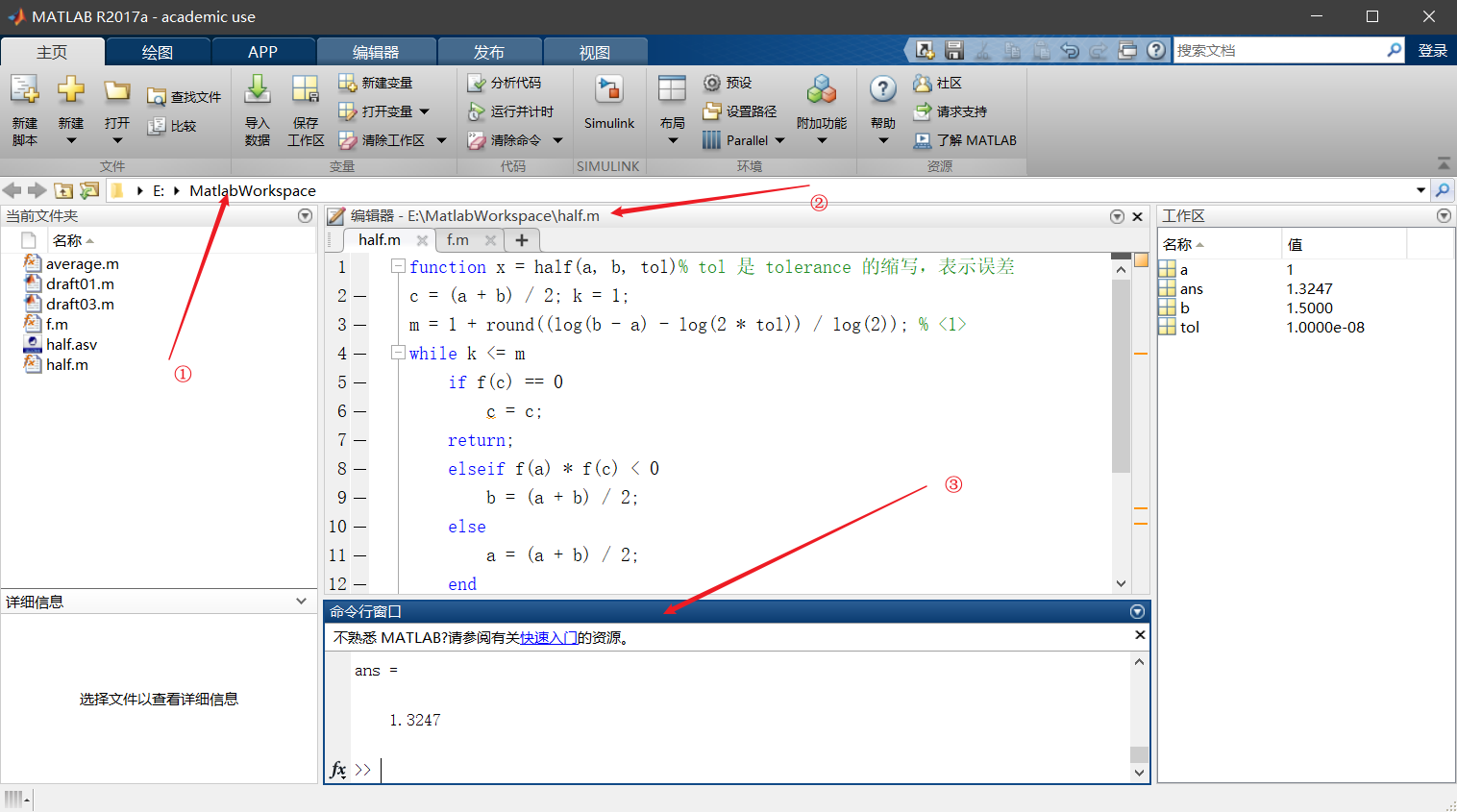
图中标注 ① 是工作目录,即代码存放的目录;标注 ② 是编辑器,即我们写代码的地方;标注 ③ 是命令行,是我们执行语句的地方。本次实验我们是在这里执行二分法的函数。
例题: 应用二分法求解方程 (x^3 - x - 1 = 0) 在区间 ([1, 1.5]) 内的数值解 (x_k),要求绝对误差小于 (10^{-8}).
解答 如下。
代码:
half.m 脚本:
function x = half(a, b, tol)% tol 是 tolerance 的缩写,表示绝对误差
c = (a + b) / 2; k = 1;
m = 1 + round((log(b - a) - log(2 * tol)) / log(2)); % <1>
while k <= m
if f(c) == 0
c = c;
return;
elseif f(a) * f(c) < 0
b = (a + b) / 2;
else
a = (a + b) / 2;
end
c = (a + b) / 2; k = k + 1;
end
x = c; % 这里加分号是为了不再命令行中输出
k % 不加分号就会在控制台输出
c
f.m 脚本,这是 half.m 中调用的 f() 函数。
function y = f(x)
y = x^3 - x -1;
然后我们在命令行执行:
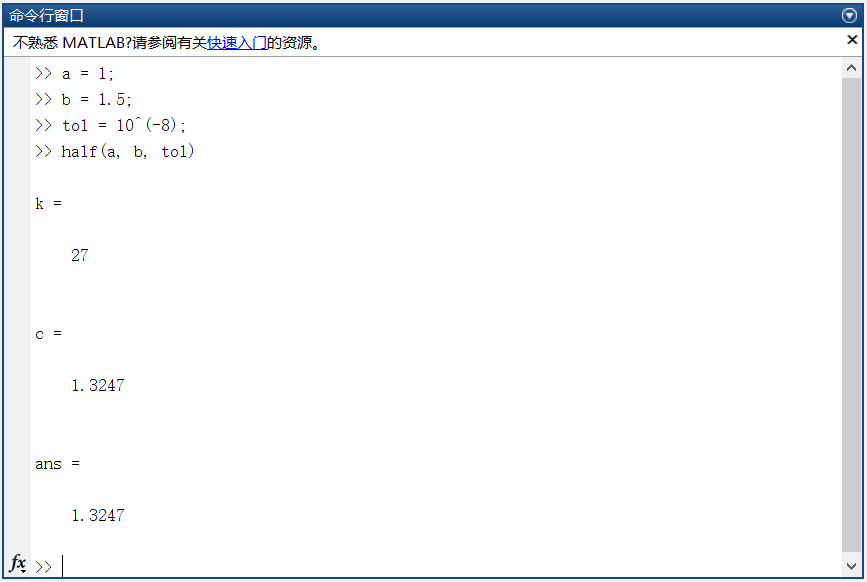
可以看出,最后求解得到的 (x = 1.3247),即输出的 ans,迭代次数 (k = 27).
关于代码 half.m 中的标注 <1>,有如下解释:


注意,在 Matlab 中,log() 函数的底是 (e).
补充例题(感兴趣的朋友可以自行测试):
