1、准备:
(1)先验概率:根据以往经验和分析得到的概率,也就是通常的概率,在全概率公式中表现是“由因求果”的果
(2)后验概率:指在得到“结果”的信息后重新修正的概率,通常为条件概率(但条件概率不全是后验概率),在贝叶斯公式中表现为“执果求因”的因
例如:加工一批零件,甲加工60%,乙加工40%,甲有0.1的概率加工出次品,乙有0.15的概率加工出次品,求一个零件是不是次品的概率即为先验概率,已经得知一个零件是次品,求此零件是甲或乙加工的概率是后验概率
(3)全概率公式:设E为随机试验,B1,B2,....Bn为E的互不相容的随机事件,且P(Bi)>0(i=1,2....n), B1 U B2 U....U Bn = S,若A是E的事件,则有
P(A) = P(B1)P(A|B1)+P(B2)P(A|B2)+.....+P(Bn)P(A|Bn)
(4)贝叶斯公式:设E为随机试验,B1,B2,....Bn为E的互不相容的随机事件,且P(Bi)>0(i=1,2....n), B1 U B2 U....U Bn = S,E的事件A满足P(A)>0,则有
P(Bi|A) = P(Bi)P(A|Bi)/(P(B1)P(A|B1)+P(B2)P(A|B2)+.....+P(Bn)P(A|Bn))
(5)条件概率公式:P(A|B) = P(AB)/P(B)
(6)极大似然估计:极大似然估计在机器学习中想当于经验风险最小化,(离散分布)一般流程:确定似然函数(样本的联合概率分布),这个函数是关于所要估计的参数的函数,然后对其取对数,然后求导,在令导数等于0的情况下,求得参数的值,此值便是参数的极大似然估计
注:经验风险:在度量一个模型的好坏,引入了损失函数,常见的损失函数有:0-1损失函数、平方损失函数、绝对损失函数、对数损失函数等,同时风险函数(期望风险)是对损失函数的期望,期望风险是关于联合分布的理论期望,但是理论的联合分布是无法求得的,只能利用样本来估计期望,因此引入经验风险,经验风险就是样本的平均损失,根据大数定理在样本趋于无穷大的时候,这个时候经验风险会无限趋近与期望风险
2、朴素贝叶斯算法
(1)思路:朴素贝叶斯算法的朴素在于对与特征之间看作相互独立的意思例如:输入向量(X1, X2,....,Xn)的各个元素是相互独立的,因此计算概率P(X1=x1,X2=x2,....Xn=xn)=P(X1=x1)P(X2=x2)......P(Xn=xn),其次基于贝叶斯定理,对于给定的训练数据集,首先基于特征条件独立假设学习联合概率分布,然后基于此模型,对于给定的输入向量,利用贝叶斯公式求出后验概率最大的输出分类标签
(2)详细:以判断输入向量x的类别的计算过程来具体说下朴素贝叶斯计算过程
<1>要计算输入向量x的类别,即是求在x的条件下的y的概率,当y取某值最大概率,则此值便为x的分类,则概率为P(Y=ck|X=x)
<2>利用条件概率公式推导贝叶斯公式(此步非必要,本人在记贝叶斯公式时习惯这么记)
由条件概率公式得P(Y=ck|X=x) = P(Y=ck,X=x)/P(X=x) = P(X=x | Y=ck)P(Y=ck)/P(X=x)
由全概率公式可得(替换P(X=x)):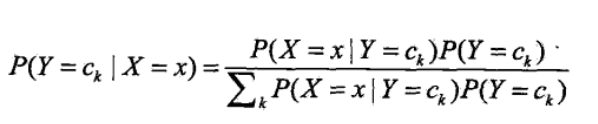
<3>由于朴素贝叶斯的“朴素”,特征向量之间是相互独立的,因此可得如下公式:
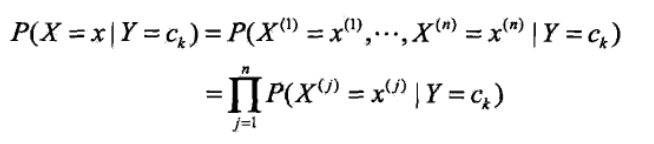
<4>将<3>中的公式带入<2>中的贝叶斯公式可得:
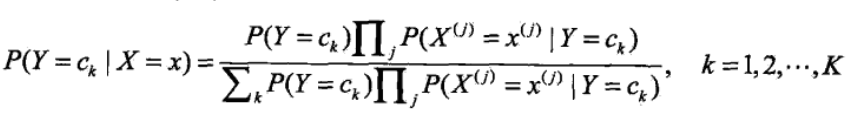
<5>看上式的分母,对于给定的输入向量X,以及Y的所有取值,全部都用了,详细的讲即为无论是计算在向量x条件下的任意一个Y值 ck,k=1,2....K,向量和c1.....ck都用到了,因此影响P(Y=ck|X=x)大小只有分子起作用,因此可得
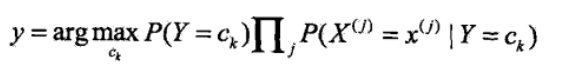
注:argmax指的是取概率最大的ck
<6>其实到<5>朴素贝叶斯的整个过程已经完毕,但是其中的P(Y=ck)和P(X(j)=x(j)|Y=ck)的求解方法并没有说,二者得求解是根据极大似 然估计法来得其概率,即得如下公式:
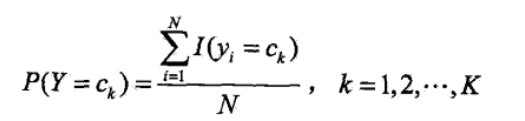
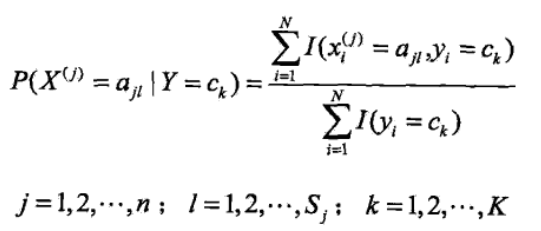
其中的I(..)是指示函数,当然这些概率在实际中可以很块求得,可以看如下得一个题,看完之后就知道这两个概率是怎么求了,公式推导 过程不赘述(具体过程我也不太清楚,不过看作类似二项分布得极大似然求值)
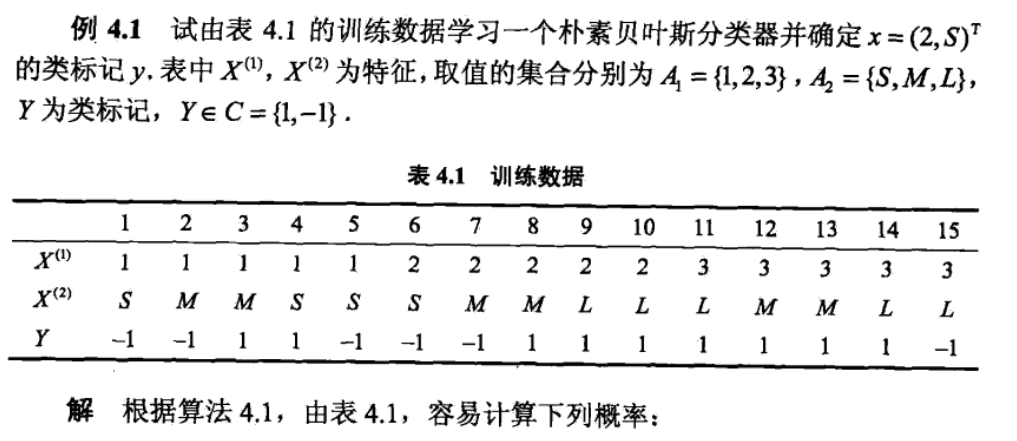
3、题-----一看就把上边得串起来了(直接贴图)