熵、相对熵和交叉熵

在学习人工智能实践：Tensorflow笔记曹健老师的视频时候，老师讲解了交叉熵这个概念，下面简要说明一下我的学习过程以及个人理解；

首先了解一下信息量：

所谓信息量是指从N个相等可能事件中选出一个事件所需要的信息度量或含量，也就是在辩识N个事件中特定的一个事件的过程中所需要提问"是或否"的最少次数。

假设X是一个离散型随机变量，其取值集合为X，概率分布函数为p(x)=Pr(X=x),x∈X，我们定义事件X=x0的信息量为： I(x0)=−log(p(x0))，可以理解为，一个事件发生的概率越大，则它所携带的信息量就越小，而当p(x0)=1时，熵将等于0，也就是说该事件的发生不会导致任何信息量的增加。举个例子，小明平时不爱运动，小明去运动的可能很小，而小王是个爱运动，经常去运动，所以我们可以做如下假设： 

　　事件A：小明今天去运动，对应的概率P(xA)=0.1，信息量为I(xA)=−log(0.1)=3.3219 

　　事件B：小王今天去运动，对应的概率P(xB)=0.999，信息量为I(xB)=−log(0.999)=0.0014 

　　可以看出，结果非常符合直观：小明今天去运动，因此如果某次去运动了（小明的朋友一定会讨论小明运动的原因），必然会引入较大的信息量，对应的I值也较高。而对于小王而言，去运动是大概率事件，在事件B发生前，大家普遍认为事件B的发生几乎是确定的，因此当某天小王去运动这个事件发生时并不会引入太多的信息量，相应的I值也非常的低。

这就可以理解成大概率事件的信息量少，而小概率事件的信息量多，因为当小概率事件发生时，一定是出现了某些信息；

       从信息传播的角度来看，信息熵可以表示信息的价值。为了求得信息的价值，我们通过求信息期望的方式，来求得信息熵。

          对于一个随机变量X而言，它的所有可能取值的信息量的期望E[I(x)]）就称为熵

公式如下：

            

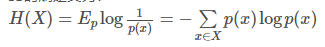
其中，x表示随机变量，与之相对应的是所有可能输出的集合，定义为符号集,随机变量的输出用x表示。P(x)表示输出概率函数。变量的不确定性越大，熵也就越大，把它搞清楚所需要的信息量也就越大。为了保证有效性，这里约定当p(x)→0时,有p(x)logp(x)→0 。

熵其实是信息量的期望值，它是一个随机变量的确定性的度量。熵越大，变量的取值越不确定，反之就越确定。

什么是交叉熵？

        信息论中，交叉熵是表示两个概率分布p,q，其中p表示真实分布，q表示非真实分布，在相同的一组事件中，其中，用非真实分布q来表示某个事件发生所需要的平均比特数。从这个定义中，我们很难理解交叉熵的定义。

　　假设现在有一个样本集中两个概率分布p,q，其中p为真实分布，q为非真实分布。

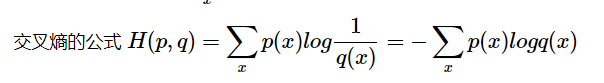
交叉熵的计算方式还可以变为：

 

用相对熵来表示交叉熵

1. 信息熵是衡量随机变量分布的混乱程度，是随机分布各事件发生的信息量的期望值，随机变量的取值个数越多，状态数也就越多，信息熵就越大，混乱程度就越大。当随机分布为均匀分布时，熵最大；信息熵推广到多维领域，则可得到联合信息熵；条件熵表示的是在 XX 给定条件下，YY 的条件概率分布的熵对 XX的期望。
2. 相对熵可以用来衡量两个概率分布之间的差异。
3. 交叉熵可以来衡量在给定的真实分布下，使用非真实分布所指定的策略消除系统的不确定性所需要付出的努力的大小。

或者：

1. 信息熵是传输一个随机变量状态值所需的比特位下界（最短平均编码长度）。
2. 相对熵是指用 qq 来表示分布 pp  额外需要的编码长度。
3. 交叉熵是指用分布 qq 来表示本来表示分布 pp 的平均编码长度。

 本文参考链接：

https://www.cnblogs.com/raorao1994/p/8872073.html

https://blog.csdn.net/rtygbwwwerr/article/details/50778098