二叉树实现

树是一个非空元素的集合，其中一个元素为根，其余元素为子树，树根是唯一没有父母的元素，相同父母的孩子是兄弟。

树的高度是指树的级的个数，元素的度是指孩子的个数，叶子节点的度为0，如图所示。

二叉树是一种特殊的树，二叉树的区别如下：

（1）二叉树的每个元素正好有两棵子树，树可以有任意棵

（2）二叉树中每个元素是有序的（左右不能互换），二树是无序的

（3）二叉树允许为空（根节点=null），树不能为空（有争议）

二叉树典型结构如图所示

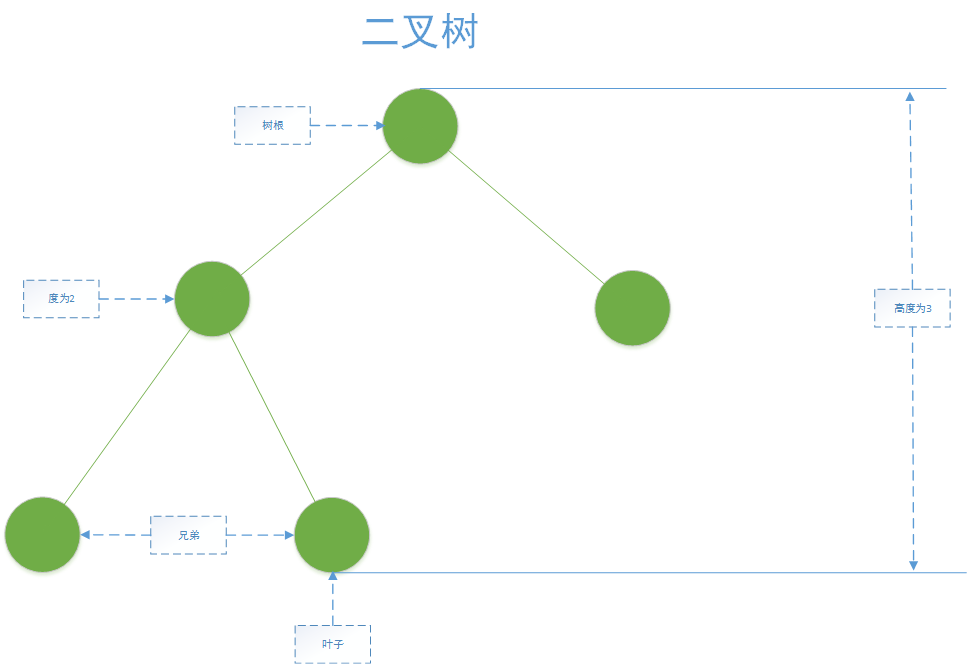
有以下特性：

（1）一棵二叉树有n个元素，有n-1条边

（2）一棵二叉树的高度为h(≥0)，则最少有h个元素，最多有2^h-1个元素

（3）一棵二叉树有n个元素(>0),二叉树的最大高度是n，最小高度是log2(n+1)

（4）叶子节点数目=度为2的节点数目+1

二叉树可以采用链表描述和数组描述

采用链表描述：

采用链表描述需要首先描述单个节点，每个节点需要保持的信息包括左孩子、有孩子和元素值，左孩子和右孩子可以用指针描述，代码如下：

class BinaryTreeNode{
        public BinaryTreeNode left, right;//左子数，右子数
        int val;//节点元素
        //提供不同的初始化函数
        public BinaryTreeNode(){
            left = right = null;
        }
        public BinaryTreeNode(int val){
            this.val = val;
            left = right = null;
        }
        public BinaryTreeNode(int val, BinaryTreeNode left, BinaryTreeNode right){
            this.val = val;
            this.left = left;
            this.right = right;
        }
    }

然后实现二叉树的操作，二叉树需要实现的操作有元素的增删改查以及打印等信息，二叉树主要实现功能如下：

public class BinaryTree {
	private BinaryTreeNode root;
	private int treeSize; 
	
	class BinaryTreeNode{
		public BinaryTreeNode left, right;//左子数，右子数
		int val;//节点元素
		//提供不同的初始化函数
		public BinaryTreeNode(){
			left = right = null;
		}
		public BinaryTreeNode(int val){
			this.val = val;
			left = right = null;
		}
		public BinaryTreeNode(int val, BinaryTreeNode left, BinaryTreeNode right){
			this.val = val;
			this.left = left;
			this.right = right;
		}
	}
	
	//前序遍历
	public void preOrder(BinaryTreeNode binaryTreeNode){
		
	}
	
	//中序遍历
	public void inOrder(BinaryTreeNode binaryTreeNode){

	}
	
	//后续遍历
	public void postOrder(BinaryTreeNode binaryTreeNode){

	}
	
	//层次遍历
	public void levelOrder(BinaryTreeNode binaryTreeNode){
		
	}
	
	//返回节点数目
	public final int size(){
		return treeSize;
	}
	
	//检查是树否为空
	public final boolean  isEmpty()  {
		return treeSize == 0;
	}
	
	//确定二叉树的高度
	public int heightRoot(){
		
	}
	
	//查找结点
	public BinaryTreeNode find(int value){
		
		return current;
	}
	
	//增加节点
	public void insert(int value){
		
	}
	
	//查找最小值
	public int minimum(){

	}
	
	//根据值，删除节点
	public boolean delete(int value){
			
		return true;
	} 
	
}

　　在所有功能中，节点的数目以及检查树是否为空代码较为简单不做叙述，其他功能实现方式如下。

前序遍历（DLR）：又叫先跟遍历，属于深度优先遍历，遍历方式是根->左->右

中序遍历(LDR)：又叫中跟遍历，属于深度优先遍历，遍历方式是左->根->右

后续遍历（LRD）：又叫后根遍历，属于深度优先遍历，遍历方式是左->右->根

层次遍历:属于广度优先遍历，自上而下，自左向右逐层遍历节点。

各个遍历方式如下图所示：

前序遍历反映了深度优先搜索的思想，沿着二叉树的枝干从左到右游历一圈就是前序遍历，如图所示。

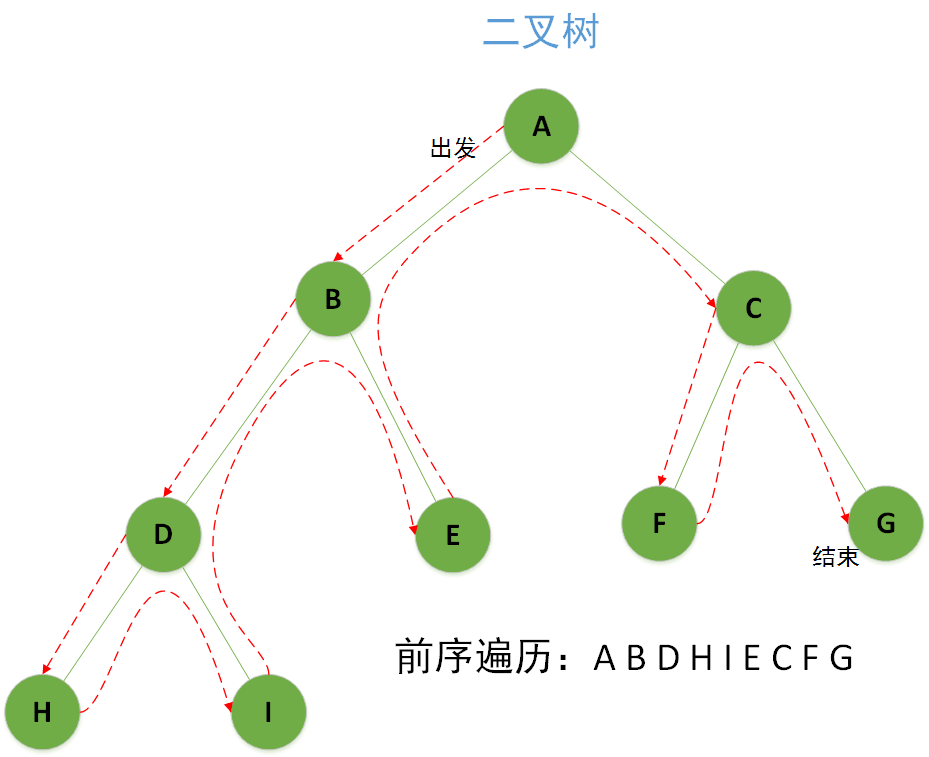
中序遍历能够应用在BST（Binary Sort Tree|二叉排序树）中，遍历出来的结果一定是有序的，对于一个二叉树进行垂直投影也可以得到中序遍历结果，如图所示：

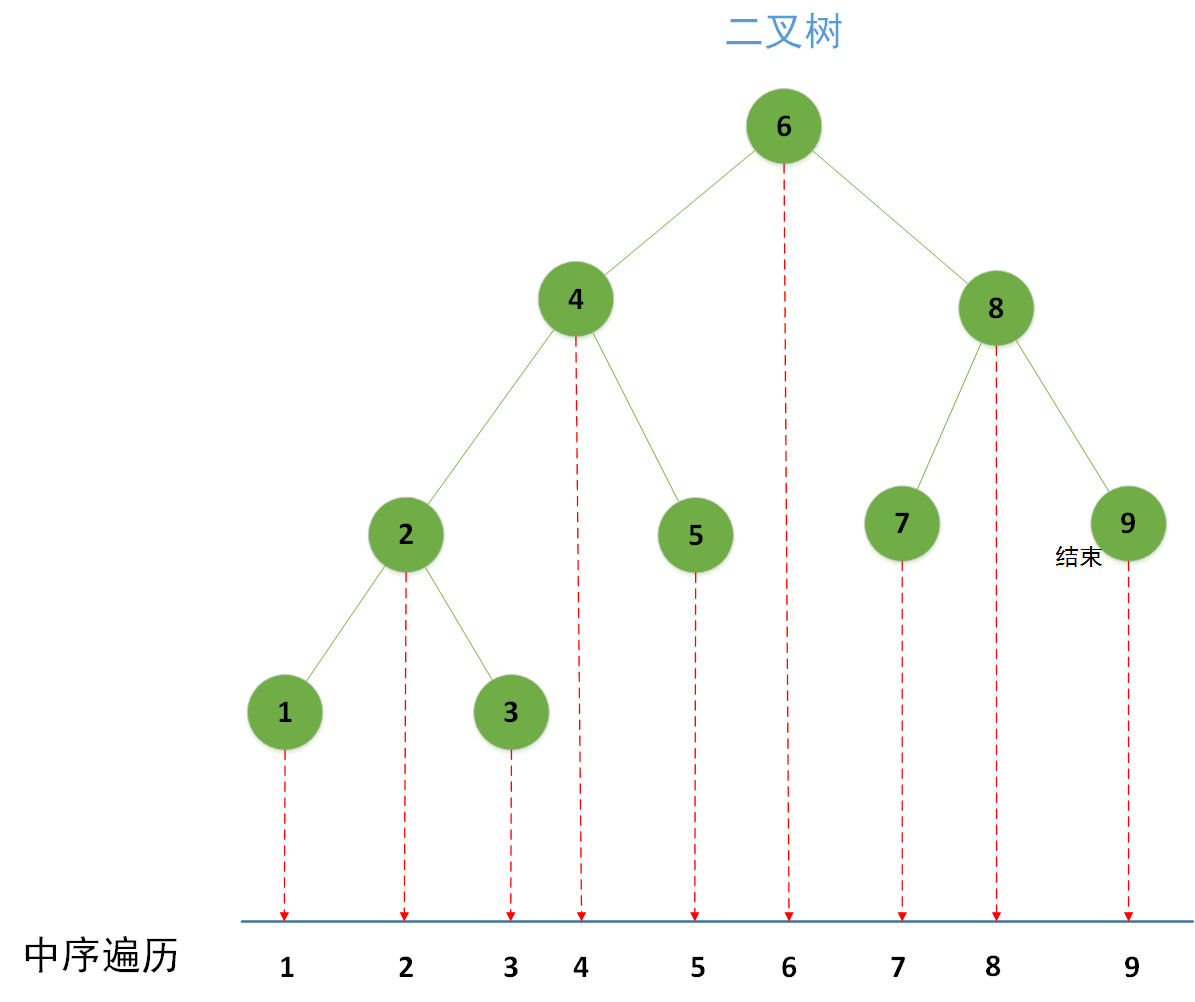
此外，中序遍历还可以用于表示中缀表达式，后续遍历可以用于后缀表达式，效果如图所示：

层次遍历，层次遍历反应的是广度优先搜索思想，对于四种遍历方式，知道任意一种不能唯一的确定数据结构，如果知道中序遍历和另外任意一种遍历方式，就能够唯一的确定一棵树。

前序遍历、中序遍历和后续遍历的实现代码如下：

//前序遍历
	public void preOrder(int binaryTreeNode){
		//前序遍历二叉树
		if(binaryTreeNode >= 0 && binaryTreeNode < treeSize){
			visitTreeNode(binaryTreeNode);
			preOrder(2*binaryTreeNode+1);
			preOrder(2*binaryTreeNode+2);
		}
	}
	
	//中序遍历
	public void inOrder(int binaryTreeNode){
		//中序遍历二叉树
		if(binaryTreeNode >= 0 && binaryTreeNode < treeSize){
			inOrder(2*binaryTreeNode+1);
			visitTreeNode(binaryTreeNode);
			inOrder(2*binaryTreeNode+2);
		}
	}
	
	//后续遍历
	public void postOrder(int binaryTreeNode){
		//后续遍历二叉树
		if(binaryTreeNode >= 0 && binaryTreeNode < treeSize){
			postOrder(2*binaryTreeNode+1);
			postOrder(2*binaryTreeNode+2);
			visitTreeNode(binaryTreeNode);
		}
	}

　　层次遍历的实现方式稍微复杂，层次遍历首先需要记录每一层的换行的地方，我们可以采用nlast指针始终指向最右的节点来实现，其次需要将每一层的节点依次打印，我们可以借助链表实现，整体的访问过程如下图所示：

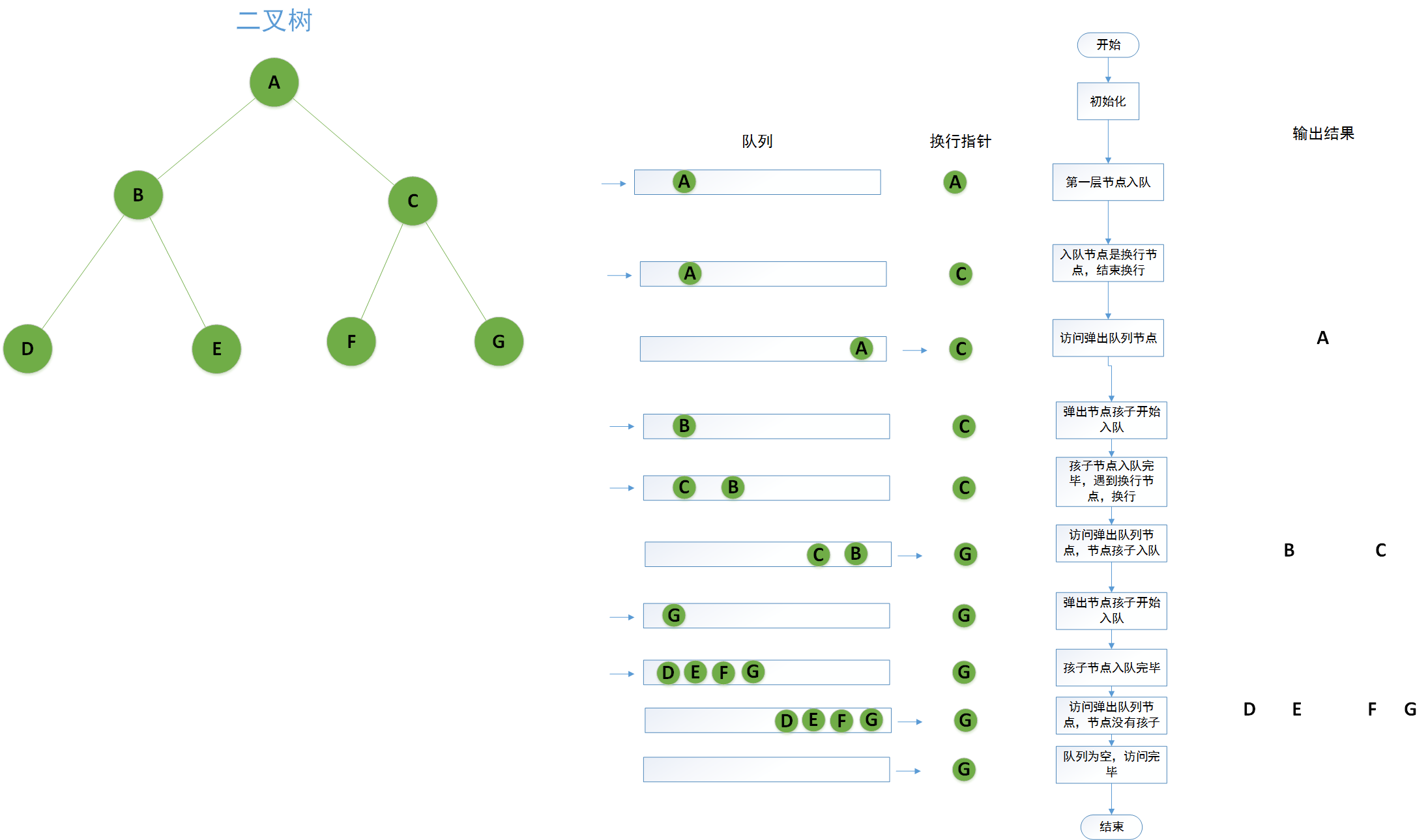
代码实现如下：

//层次遍历
	public void levelOrder(BinaryTreeNode binaryTreeNode){
		//层次遍历二叉树
		Queue<BinaryTreeNode> nodeQueue = new LinkedList<BinaryTreeNode>();
		BinaryTreeNode last=binaryTreeNode;
		BinaryTreeNode nlast=binaryTreeNode;
		while(binaryTreeNode != null){
			visitTreeNode(binaryTreeNode);
			last = binaryTreeNode;
			//将孩子加入队列
			if(binaryTreeNode.left != null){
				nodeQueue.offer(binaryTreeNode.left);
			}
			if(binaryTreeNode.right != null){
				nodeQueue.offer(binaryTreeNode.right);
			}
			//提取下一个要访问的节点
			if(nodeQueue.isEmpty() == true){
				return;//此处可以退出循环
			}
			binaryTreeNode = nodeQueue.poll();
			if(last == nlast){
				//该层打印结束，需要换行
				System.out.println();
				if(nlast.right != null){
					nlast = nlast.right;
				}
			}
			
		}
	}

　　树的高度确定只需要递归判定左右子树的高度即可，实现代码如下：

//确定二叉树的高度
	public int heightRoot(){
		return height(root);
	}
	
	private int height(BinaryTreeNode binaryTreeNode){
		int hl, hr;//左树高度，右树高度
		if(binaryTreeNode == null){
			return 0;
		}
		hl = height(binaryTreeNode.left);
		hr = height(binaryTreeNode.right);
		if(hl > hr)
			return ++hl;
		else
			return ++hr;
	}

　　节点的插入：插入节点从根节点出发，如果小于根节点，就向左子树移动，与左孩子比较，如果大于根节点就向右子树移动，与有孩子比较，知道遇到空节点，放到该位置，实现代码如下：

//增加节点
	public void insert(int value){
		BinaryTreeNode node = new BinaryTreeNode(value);
		if(root == null){
			//将增加的节点设置为根节点
			root = node;
		}else{
			BinaryTreeNode current = root;
			BinaryTreeNode parent = root;
			while(current != null){
				parent = current;//记录父类信息，防止丢失父类信息
				if(value < current.val){
					current = current.left;
				}else{
					current = current.right;
				}
			}
			if(value < parent.val){
				parent.left = node;
			}else{
				parent.right = node;
			}
		}
		treeSize++;
	}

　　查找最小值：根据二叉树的插入方式可以看出，该二叉树属于二叉查找树，所有节点都满足左子树<该节点<右子树，因此我们按照这个顺序查找最小值即可，代码如下。同理，也可以查找最大值。

	//查找最小值
	public int minimum(){
		BinaryTreeNode current = new BinaryTreeNode();
		current = root;
		while(current.left != null){
			current = current.left;
		}
		return current.val;
	}

　　查找结点：根据查找二叉树的性质查找即可，代码如下

//查找结点
	public BinaryTreeNode find(int value){
		BinaryTreeNode current = root;
		while(value != current.val){
			if(value < current.val){
				current = current.left;
			}else{
				current = current.right;
			}
			if(current == null)
				return null;//没有找到
		}
		return current;
	}

　　删除节点：对于二叉树来说，删除节点最为复杂，删除节点首先要查找结点，按照节点二叉树的特性首先找到要删除的节点，查找的代码如下：

BinaryTreeNode current;
		BinaryTreeNode parent = new BinaryTreeNode();
		boolean isLeftTrue = false;
		current = root;
		//首先查找这个节点
		while(current.val != value){
			parent = current;//保存父类信息
			if(value < current.val){
				current = current.left;
				isLeftTrue = true;
			}else{
				current = current.right;
				isLeftTrue = false;
			}
			if(current == null){
				//判断是否找到
				return false;
			}
		}

　　然后根据要删除节点的情况分为四种情况，分别是没有孩子的节点（叶子）、有左孩子的节点、有有孩子的节点和有两个孩子的节点。

对于没有孩子的节点，直接删除即可

//删除一个子节点的情况
		if(current.left == null && current.right == null){
			//节点是叶子节点
			if(current == root)//判断是根节点
				root = null;
			else if(isLeftTrue)//删除左节点
				parent.left = null;
			else//删除右节点
				parent.right = null;
		}

　　对于只有一个孩子的节点，先删除该节点，然后将该孩子节点直接放到该节点的位置即可，代码如下：

else if(current.left == null){
			//只有右节点
			if(current == root)//判断是根节点
				root = null;
			else if(isLeftTrue)//删除左节点
				parent.left = current.right;
			else//删除右节点
				parent.right = current.right;
		}else if(current.right == null){
			//只有左节点
			if(current == root)//判断是根节点
				root = null;
			else if(isLeftTrue)//删除左节点
				parent.left = current.left;
			else//删除右节点
				parent.right = current.left;
		}

　　对于两个孩子的节点，首先要找到后继节点，然后将后继节点来代替该节点即可，所谓后续节点即也就是中序后继（比这个节点大一点的数），对于某一结点的后继节点一定存在于右子树，因为只有右子树比这个节点大，然后找大的最少的树，寻找右子树的最小值即可（沿着左孩子寻找即可）。寻找后继节点的代码如下：

//查找后继节点
	private BinaryTreeNode getSuccessor(BinaryTreeNode delNode){
		
		BinaryTreeNode current = delNode.right;//先定位到右子树
		BinaryTreeNode parent = delNode;
		//寻找右子树的最小值
		while(current.left!=null){
			parent = current;
			current = current.left;
		}
		//如果继点有分支（一定是右分支）,因为这个继点要移动到删除节点的位置，需要将继点的右分支放在继点的位置
		if(current != delNode.right){
			parent.left = current.right;//继点的右分支放在继点的位置
			current.right = delNode.right;//将继点放到删除节点的位置
		}
		return current;
	}

　　然后将继点放在删除的节点位置即可，代码如下：

else{
			//有两个分支节点
			BinaryTreeNode successor = getSuccessor(current);
			if(current == root){
				root = successor;
			}else if(isLeftTrue){
				parent.left = successor;
			}else{
				parent.right = successor;
			}
			successor.left = current.left;
		}

　　二叉树删除节点的整体代码如下：

//根据值，删除节点
	public boolean delete(int value){
		BinaryTreeNode current;
		BinaryTreeNode parent = new BinaryTreeNode();
		boolean isLeftTrue = false;
		current = root;
		//首先查找这个节点
		while(current.val != value){
			parent = current;//保存父类信息
			if(value < current.val){
				current = current.left;
				isLeftTrue = true;
			}else{
				current = current.right;
				isLeftTrue = false;
			}
			if(current == null){
				//判断是否找到
				return false;
			}
		}
		
		//删除一个子节点的情况
		if(current.left == null && current.right == null){
			//节点是叶子节点
			if(current == root)//判断是根节点
				root = null;
			else if(isLeftTrue)//删除左节点
				parent.left = null;
			else//删除右节点
				parent.right = null;
		}else if(current.left == null){
			//只有右节点
			if(current == root)//判断是根节点
				root = null;
			else if(isLeftTrue)//删除左节点
				parent.left = current.right;
			else//删除右节点
				parent.right = current.right;
		}else if(current.right == null){
			//只有左节点
			if(current == root)//判断是根节点
				root = null;
			else if(isLeftTrue)//删除左节点
				parent.left = current.left;
			else//删除右节点
				parent.right = current.left;
		}else{
			//有两个分支节点
			BinaryTreeNode successor = getSuccessor(current);
			if(current == root){
				root = successor;
			}else if(isLeftTrue){
				parent.left = successor;
			}else{
				parent.right = successor;
			}
			successor.left = current.left;
		}
			
		return true;
	} 
	
	//查找后继节点
	private BinaryTreeNode getSuccessor(BinaryTreeNode delNode){
		
		BinaryTreeNode current = delNode.right;//先定位到右子树
		BinaryTreeNode parent = delNode;
		//寻找右子树的最小值
		while(current.left!=null){
			parent = current;
			current = current.left;
		}
		//如果继点有分支（一定是右分支）,因为这个继点要移动到删除节点的位置，需要将继点的右分支放在继点的位置
		if(current != delNode.right){
			parent.left = current.right;//继点的右分支放在继点的位置
			current.right = delNode.right;//将继点放到删除节点的位置
		}
		return current;
	}

　　二叉树所有代码及测试程序如下所示：

package dataStructure;

import java.util.LinkedList;
import java.util.Queue;



public class BinaryTree {
	private BinaryTreeNode root;
	private int treeSize; 
	
	class BinaryTreeNode{
		public BinaryTreeNode left, right;//左子数，右子数
		int val;//节点元素
		//提供不同的初始化函数
		public BinaryTreeNode(){
			left = right = null;
		}
		public BinaryTreeNode(int val){
			this.val = val;
			left = right = null;
		}
		public BinaryTreeNode(int val, BinaryTreeNode left, BinaryTreeNode right){
			this.val = val;
			this.left = left;
			this.right = right;
		}
	}
	
	//访问一个节点
	private void visitTreeNode(BinaryTreeNode binaryTreeNode){
		System.out.print(binaryTreeNode.val+" ");
	}
	
	//前序遍历
	public void preOrder(BinaryTreeNode binaryTreeNode){
		//前序遍历二叉树
		if(binaryTreeNode != null){
			visitTreeNode(binaryTreeNode);
			preOrder(binaryTreeNode.left);
			preOrder(binaryTreeNode.right);
		}
	}
	
	//中序遍历
	public void inOrder(BinaryTreeNode binaryTreeNode){
		//中序遍历二叉树
		if(binaryTreeNode != null){
			inOrder(binaryTreeNode.left);
			visitTreeNode(binaryTreeNode);
			inOrder(binaryTreeNode.right);
		}
	}
	
	//后续遍历
	public void postOrder(BinaryTreeNode binaryTreeNode){
		//后续遍历二叉树
		if(binaryTreeNode != null){
			postOrder(binaryTreeNode.left);
			postOrder(binaryTreeNode.right);
			visitTreeNode(binaryTreeNode);
		}
	}
	
	//层次遍历
	public void levelOrder(BinaryTreeNode binaryTreeNode){
		//层次遍历二叉树
		Queue<BinaryTreeNode> nodeQueue = new LinkedList<BinaryTreeNode>();
		BinaryTreeNode last=binaryTreeNode;
		BinaryTreeNode nlast=binaryTreeNode;
		while(binaryTreeNode != null){
			visitTreeNode(binaryTreeNode);
			last = binaryTreeNode;
			//将孩子加入队列
			if(binaryTreeNode.left != null){
				nodeQueue.offer(binaryTreeNode.left);
			}
			if(binaryTreeNode.right != null){
				nodeQueue.offer(binaryTreeNode.right);
			}
			//提取下一个要访问的节点
			if(nodeQueue.isEmpty() == true){
				return;//此处可以退出循环
			}
			binaryTreeNode = nodeQueue.poll();
			if(last == nlast){
				//该层打印结束，需要换行
				System.out.println();
				if(nlast.right != null){
					nlast = nlast.right;
				}
			}
			
		}
	}
	
	//返回节点数目
	public final int size(){
		return treeSize;
	}
	
	//检查是树否为空
	public final boolean  isEmpty()  {
		return treeSize == 0;
	}
	
	//确定二叉树的高度
	public int heightRoot(){
		return height(root);
	}
	
	private int height(BinaryTreeNode binaryTreeNode){
		int hl, hr;//左树高度，右树高度
		if(binaryTreeNode == null){
			return 0;
		}
		hl = height(binaryTreeNode.left);
		hr = height(binaryTreeNode.right);
		if(hl > hr)
			return ++hl;
		else
			return ++hr;
	}
	
	//查找结点
	public BinaryTreeNode find(int value){
		BinaryTreeNode current = root;
		while(value != current.val){
			if(value < current.val){
				current = current.left;
			}else{
				current = current.right;
			}
			if(current == null)
				return null;//没有找到
		}
		return current;
	}
	
	//增加节点
	public void insert(int value){
		BinaryTreeNode node = new BinaryTreeNode(value);
		if(root == null){
			//将增加的节点设置为根节点
			root = node;
		}else{
			BinaryTreeNode current = root;
			BinaryTreeNode parent = root;
//			while(true){ 
//				if(value < parent.val){
//					current = parent.left;
//					if(current == null){
//						parent.left = node;//插入节点
//						return;
//					}else{
//						parent = parent.left;
//					}
//				}else{
//					current = parent.right;
//					if(current == null){
//						parent.right = node;//插入节点
//						return;
//					}else{
//						parent = parent.right;
//					}
//				}
//			}
			while(current != null){
				parent = current;//记录父类信息，防止丢失父类信息
				if(value < current.val){
					current = current.left;
				}else{
					current = current.right;
				}
			}
			if(value < parent.val){
				parent.left = node;
			}else{
				parent.right = node;
			}
		}
		treeSize++;
	}
	
	//查找最小值
	public int minimum(){
		BinaryTreeNode current = new BinaryTreeNode();
		current = root;
		while(current.left != null){
			current = current.left;
		}
		return current.val;
	}
	
	//根据值，删除节点
	public boolean delete(int value){
		BinaryTreeNode current;
		BinaryTreeNode parent = new BinaryTreeNode();
		boolean isLeftTrue = false;
		current = root;
		//首先查找这个节点
		while(current.val != value){
			parent = current;//保存父类信息
			if(value < current.val){
				current = current.left;
				isLeftTrue = true;
			}else{
				current = current.right;
				isLeftTrue = false;
			}
			if(current == null){
				//判断是否找到
				return false;
			}
		}
		
		//删除一个子节点的情况
		if(current.left == null && current.right == null){
			//节点是叶子节点
			if(current == root)//判断是根节点
				root = null;
			else if(isLeftTrue)//删除左节点
				parent.left = null;
			else//删除右节点
				parent.right = null;
		}else if(current.left == null){
			//只有右节点
			if(current == root)//判断是根节点
				root = null;
			else if(isLeftTrue)//删除左节点
				parent.left = current.right;
			else//删除右节点
				parent.right = current.right;
		}else if(current.right == null){
			//只有左节点
			if(current == root)//判断是根节点
				root = null;
			else if(isLeftTrue)//删除左节点
				parent.left = current.left;
			else//删除右节点
				parent.right = current.left;
		}else{
			//有两个分支节点
			BinaryTreeNode successor = getSuccessor(current);
			if(current == root){
				root = successor;
			}else if(isLeftTrue){
				parent.left = successor;
			}else{
				parent.right = successor;
			}
			successor.left = current.left;
		}
			
		return true;
	} 
	
	//查找后继节点
	private BinaryTreeNode getSuccessor(BinaryTreeNode delNode){
		
		BinaryTreeNode current = delNode.right;//先定位到右子树
		BinaryTreeNode parent = delNode;
		//寻找右子树的最小值
		while(current.left!=null){
			parent = current;
			current = current.left;
		}
		//如果继点有分支（一定是右分支）,因为这个继点要移动到删除节点的位置，需要将继点的右分支放在继点的位置
		if(current != delNode.right){
			parent.left = current.right;//继点的右分支放在继点的位置
			current.right = delNode.right;//将继点放到删除节点的位置
		}
		return current;
	}
	
	public static void main(String[] args){
		BinaryTree tree = new BinaryTree();
//		二叉树结构如下
//				    10 
//			  6             15 
//		  4      8       12      18 
//		1   5   7  9   11 13    16 19 		
		tree.insert(10);
		tree.insert(6); 
		tree.insert(15);
		tree.insert(4);
		tree.insert(8);
		tree.insert(1);
		tree.insert(5);
		tree.insert(7);
		tree.insert(9);
		tree.insert(12);
		tree.insert(18);
		tree.insert(11);
		tree.insert(13);
		tree.insert(16);
		tree.insert(19);

		System.out.println("
前序遍历");
		tree.preOrder(tree.root);
		System.out.println("
中序遍历");
		tree.inOrder(tree.root);
		System.out.println("
后序遍历");
		tree.postOrder(tree.root);
		System.out.println("
层次遍历");
		tree.levelOrder(tree.root);
		System.out.println("
寻找"+tree.find(10).val);
		tree.delete(8);
		tree.levelOrder(tree.root);
		System.out.println("
");
		tree.delete(11); 
		tree.levelOrder(tree.root);
		System.out.println("
");
		tree.delete(12); 
		tree.levelOrder(tree.root);
		System.out.println("
");
		tree.delete(4);
		tree.levelOrder(tree.root);
	}
}

　　运行结果如下：

前序遍历
10 6 4 1 5 8 7 9 15 12 11 13 18 16 19
中序遍历
1 4 5 6 7 8 9 10 11 12 13 15 16 18 19
后序遍历
1 5 4 7 9 8 6 11 13 12 16 19 18 15 10
层次遍历
10
6 15
4 8 12 18
1 5 7 9 11 13 16 19
寻找10
10
6 15
4 9 12 18
1 5 7 11 13 16 19

10
6 15
4 9 12 18
1 5 7 13 16 19

10
6 15
4 9 13 18
1 5 7 16 19

10
6 15
5 9 13 18
1 7 16 19

 此外二叉树还可与用数组实现，采用数组实现不用采用指针记录连接关系，每个节点的左节点是index*2+1，右节点是诗index*2+2，在节点删除的时候，需要手动将节点置空。采用数组实现的二叉树，会存在空间浪费，效率也不是很高，空间表示二叉树的结果如图所示：

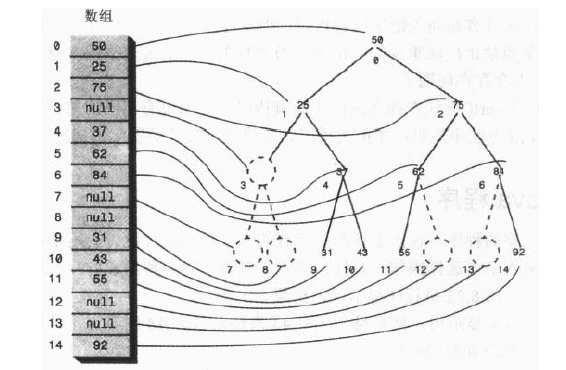
完整代码实现如下所示：

package dataStructure;

import java.util.LinkedList;
import java.util.Queue;



public class BinaryTreeInArray {
	private int root; 
	private int treeSize; 
	private int[] nodeArray = new int[30];
	
	public BinaryTreeInArray(){
		root = 0;
		treeSize = 0;
		for(int i=0; i<30; i++)
			nodeArray[i]  = -1;
	}
	//访问一个节点
	private void visitTreeNode(int binaryTreeNode){
		System.out.print(nodeArray[binaryTreeNode]+" ");
	}
	
	//前序遍历
	public void preOrder(int binaryTreeNode){
		//前序遍历二叉树
		if(binaryTreeNode >= 0 && binaryTreeNode < treeSize){
			visitTreeNode(binaryTreeNode);
			preOrder(2*binaryTreeNode+1);
			preOrder(2*binaryTreeNode+2);
		}
	}
	
	//中序遍历
	public void inOrder(int binaryTreeNode){
		//中序遍历二叉树
		if(binaryTreeNode >= 0 && binaryTreeNode < treeSize){
			inOrder(2*binaryTreeNode+1);
			visitTreeNode(binaryTreeNode);
			inOrder(2*binaryTreeNode+2);
		}
	}
	
	//后续遍历
	public void postOrder(int binaryTreeNode){
		//后续遍历二叉树
		if(binaryTreeNode >= 0 && binaryTreeNode < treeSize){
			postOrder(2*binaryTreeNode+1);
			postOrder(2*binaryTreeNode+2);
			visitTreeNode(binaryTreeNode);
		}
	}
	
	//层次遍历
	public void levelOrder(int binaryTreeNode){
		//层次遍历二叉树
		Queue<Integer> nodeQueue = new LinkedList<Integer>();
		int last=binaryTreeNode;
		int nlast=binaryTreeNode;
		while(binaryTreeNode >= 0 && binaryTreeNode < treeSize){
			visitTreeNode(binaryTreeNode);
			last = binaryTreeNode;
			//将孩子加入队列
			if(2*binaryTreeNode+1 >= 0 && 2*binaryTreeNode+1 < treeSize){
				nodeQueue.offer(2*binaryTreeNode+1);
			}
			if(2*binaryTreeNode+2 >= 0 && 2*binaryTreeNode+2 < treeSize){
				nodeQueue.offer(2*binaryTreeNode+2);
			}
			//提取下一个要访问的节点
			if(nodeQueue.isEmpty() == true){
				return;//此处可以退出循环
			}
			binaryTreeNode = nodeQueue.poll();
			if(last == nlast){
				//该层打印结束，需要换行
				System.out.println();
				if(2*nlast+2 >= 0 && 2*nlast+2 < treeSize){
					nlast = 2*nlast+2;
				}
			}
			
		}
	}
	
	//返回节点数目
	public final int size(){
		return treeSize;
	}
	
	//检查是树否为空
	public final boolean  isEmpty()  {
		return treeSize == 0;
	}
	
	//确定二叉树的高度
	public int heightRoot(){
		return height(root);
	}
	
	private int height(int binaryTreeNode){
		int hl, hr;//左树高度，右树高度
		if(binaryTreeNode <= 0 && binaryTreeNode < treeSize){
			return 0;
		}
		hl = height(2*binaryTreeNode+1);
		hr = height(2*binaryTreeNode+2);
		if(hl > hr)
			return ++hl;
		else
			return ++hr;
	}
	
	//查找结点
	public int find(int value){
		int current = root;
		while(value != nodeArray[current]){
			if(value < nodeArray[current]){
				if(2*current+1 < treeSize)
					current = nodeArray[2*current+1];
				else
					return -1;//没有找到
			}else{ 
				if(2*current+2 < treeSize)
					current = nodeArray[2*current+2];
				else
					return -1;//没有找到
			} 
		}
		return nodeArray[current];
	}
	
	//增加节点
	public void insert(int value){ 
		int node = value;
		if(nodeArray[root] == -1){
			//将增加的节点设置为根节点
			nodeArray[root] = node;
		}else{
			int current = root;
			int parent = root;
//			while(true){ 
//				if(value < nodeArray[parent]){
//					current = nodeArray[2*parent+1];
//					if(current >= 0 && current < treeSize){
//						nodeArray[2*parent+1] = node;//插入节点
//						return;
//					}else{
//						nodeArray[parent] = nodeArray[2*parent+1];
//					}
//				}else{
//					current = nodeArray[2*parent+2];
//					if(current >= 0 && current < treeSize){
//						nodeArray[2*parent+2] = node;//插入节点
//						return;
//					}else{
//						parent = nodeArray[2*parent+2];
//					}
//				}
//			}
			while(nodeArray[current] != -1){
				parent = current;//记录父类信息，防止丢失父类信息
				if(value < nodeArray[current]){
					current = 2*current + 1;
				}else{
					current = 2*current + 2;
				}
			}
			nodeArray[current] = node;
		}
		treeSize++;
	}
	
	//查找最小值
	public int minimum(){
		int current = root;
		while(nodeArray[2*current + 1] != -1){
			current = nodeArray[2*current + 1];
		}
		return nodeArray[current];
	}
	
	//根据值，删除叶子
	public boolean delete(int value){
		int current;
		int parent = -1;
		boolean isLeftTrue = false;
		current = root;
		//首先查找这个节点
		while(nodeArray[current] != value){
			parent = current;//保存父类信息
			if(value < nodeArray[current]){
				if(2*current+1 < treeSize){ 
					current = 2*current+1;
					isLeftTrue = true;
				}else
					return false;
			}else{
				if(2*current+2 < treeSize){
					current = 2*current+2;
					isLeftTrue = false;
				}else
					return false; 
			} 
		}
		
		//删除一个子节点的情况
		if(nodeArray[2*current+1] == -1 && nodeArray[2*current+2] == -1){
			//节点是叶子节点
			if(current == root)//判断是根节点
				nodeArray[root] = -1;
			else if(isLeftTrue)//删除左节点
				nodeArray[2*parent+1] = -1;
			else//删除右节点
				nodeArray[2*parent+2] = -1;
		}else if(nodeArray[2*current+1] == -1){
			//只有右节点
			if(current == root)//判断是根节点
				nodeArray[root] = nodeArray[2*current+2];
			else if(isLeftTrue)//删除左节点
				nodeArray[2*parent+1] = nodeArray[2*current+2];
			else//删除右节点
				nodeArray[2*parent+2] = nodeArray[2*current+2];
			nodeArray[2*current+2] = -1;
		}else if(nodeArray[2*current+2] == -1){
			//只有左节点
			if(current == root)//判断是根节点
				nodeArray[root] = nodeArray[2*current+1];
			else if(isLeftTrue)//删除左节点
				nodeArray[2*parent+1] = nodeArray[2*current+1];
			else//删除右节点
				nodeArray[2*parent+2] = nodeArray[2*current+1];
			nodeArray[2*current+1] = -1;
		}else{
			//有两个分支节点
			int successor = getSuccessor(current);
			if(current == root){
				nodeArray[root] = nodeArray[successor];
			}else if(isLeftTrue){
				nodeArray[2*parent+1] = nodeArray[successor];
			}else{
				nodeArray[2*parent+2] = nodeArray[successor];
			} 
			nodeArray[successor] = -1;
		}
			
		return true;
	} 
	
	//查找后继节点
	private int getSuccessor(int delNode){
		
		int current = 2*delNode+2;
		int parent = delNode;
		while(nodeArray[2*current+1] != -1){
			parent = current;
			current = 2*current+1;
		}
		//此处是删除子节点有分支的方法
//		if(current != 2*delNode+2){
//			nodeArray[2*parent+1] = nodeArray[2*current+2];//将继点的右节点连接到父类的左节点，空出继点
////			nodeArray[2*parent+2] = -1;//右
//		}
		return current;
	}
	
	public static void main(String[] args){
		BinaryTreeInArray tree = new BinaryTreeInArray();
//		二叉树结构如下
//				    10 
//			  6             15 
//		  4      8       12      18 
//		1   5   7  9   11 13    16 19 		
		tree.insert(10);
		tree.insert(6); 
		tree.insert(15);
		tree.insert(4);
		tree.insert(8);
		tree.insert(1);
		tree.insert(5);
		tree.insert(7);
		tree.insert(9);
		tree.insert(12);
		tree.insert(18);
		tree.insert(11);
		tree.insert(13);
		tree.insert(16);
		tree.insert(19);

		System.out.println("
前序遍历");
		tree.preOrder(tree.root);
		System.out.println("
中序遍历");
		tree.inOrder(tree.root);
		System.out.println("
后序遍历");
		tree.postOrder(tree.root);
		System.out.println("
层次遍历");
		tree.levelOrder(tree.root);
		System.out.println("
寻找"+tree.find(10));
		tree.delete(8);
		tree.levelOrder(tree.root);
		System.out.println("
");
		tree.delete(11); 
		tree.levelOrder(tree.root);
		System.out.println("
");
		tree.delete(12); 
		tree.levelOrder(tree.root);
		System.out.println("
");
		tree.delete(4);
		tree.levelOrder(tree.root);
	}
}

运行结果如下：

前序遍历
10 6 4 1 5 8 7 9 15 12 11 13 18 16 19
中序遍历
1 4 5 6 7 8 9 10 11 12 13 15 16 18 19
后序遍历
1 5 4 7 9 8 6 11 13 12 16 19 18 15 10
层次遍历
10
6 15
4 8 12 18
1 5 7 9 11 13 16 19
寻找10
10
6 15
4 9 12 18
1 5 7 -1 11 13 16 19

10
6 15
4 9 12 18
1 5 7 -1 -1 13 16 19

10
6 15
4 9 13 18
1 5 7 -1 -1 -1 16 19

10
6 15
5 9 13 18
1 -1 7 -1 -1 -1 16 19